Coniques circonscrites et inscrites à un triangle

Un triangle et ses ellipses de Steiner inscrite (en rouge) et circonscrite (en vert).

L'ellipse circonscrite de Steiner d'un triangle est l'ellipse passant par les trois sommets du triangle et de centre, le centre de gravité du triangle. Elle correspond à l'ellipse inscrite de Steiner du triangle anticomplémentaire.

Pour un triangle donné, elle est l'ellipse circonscrite d'aire minimale, et son aire est proportionnelle à celle du triangle[3] :

${\displaystyle {\mathcal {A}}_{\textrm {ellipse}}={\frac {4\pi {\sqrt {3}}}{9}}{\mathcal {A}}_{\textrm {triangle}}.}$

Le théorème de Brianchon-Poncelet établit qu'une hyperbole circonscrite à un triangle est équilatère si et seulement si elle passe également par l'orthocentre du triangle, et dans ce cas, son centre est sur le cercle d'Euler[4].

Hyperbole de Kiepert et ses asymptotes

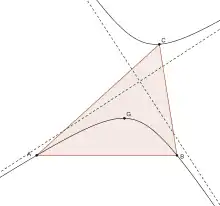
L'hyperbole de Kiepert d'un triangle est la courbe contenant tous les points de Lemoine du triangle. Elle passe par son centre de gravité.

Hyperbole de Feuerbach

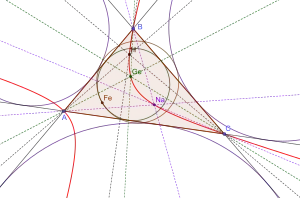
L'hyperbole de Feuerbach d'un triangle est l'hyperbole passant par les trois sommets du triangle et dont le centre de symétrie est le point de Feuerbach du triangle. Elle passe par ses points de Nagel et de Gergonne.

Hyperbole de Jerabek d'un triangle

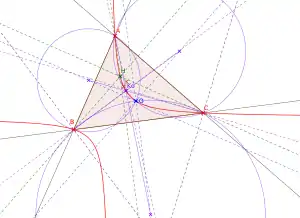
L'hyperbole de Jerabek d'un triangle est le conjugué isogonal de la droite d'Euler du triangle.

Elle passe par le centre du cercle circonscrit, l'orthocentre, le point symédian et le point de Kosnita du triangle.

Une ellipse de Steiner est inscrite dans le triangle.

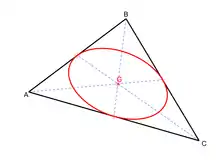
L'ellipse de Steiner d'un triangle est l'unique ellipse tangente à chacun des côtés en leur milieu. De toutes les ellipses inscrites, l'ellipse de Steiner est celle d'aire maximale.

Le centre de gravité du triangle de référence est à la fois le centre et le point de Brianchon de l'ellipse de Steiner.

L'ellipse de Steiner d'un triangle est l'ellipse circonscrite de Steiner de son triangle médian.

L'ellipse de Mandart (en rouge), touche le triangle (en noir) aux points de contact des cercles exinscrits (en gris).

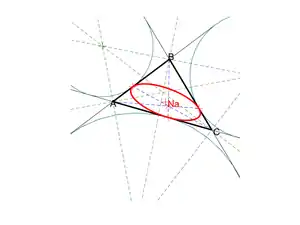
L'ellipse de Mandart d'un triangle est l'unique ellipse tangente à chacun des côtés aux points de contact des cercles exinscrits (les sommets du triangle de Nagel) ; son point de Brianchon est donc le point de Nagel du triangle[5].

Le centre de l'ellipse de Mandart est le mittenpunkt du triangle.

L'ellipse de Brocard.

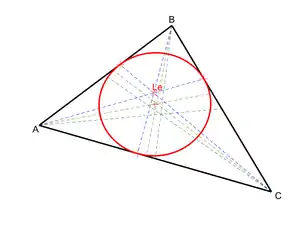
L'ellipse de Brocard d'un triangle est l'unique ellipse tangente à chacun des côtés aux sommets de son triangle symédian (le triangle formé par les points d'intersection des côtés et des symédianes du triangle).

Ses foyers sont les points de Brocard du triangle, son centre est donc au point milieu de Brocard. Son point de Brianchon est le point de Lemoine.

L'ellipse de Lemoine.

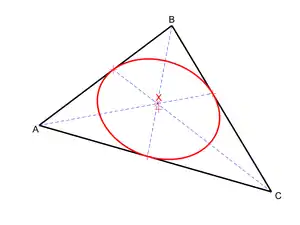
L'ellipse de Lemoine d'un triangle est l'unique ellipse tangente dont les foyers sont le centre de gravité du triangle et son point de Lemoine. Son point de Brianchon est donc le point milieu entre ces deux points.

Une conique inscrite au triangle est une parabole si et seulement si

${\displaystyle {\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=0.}$

Son foyer a alors pour coordonnées trilinéaires a/x² : b/y² : c/z² et appartient au cercle circonscrit au triangle de référence, tandis que l'orthocentre est sur la droite directrice. Formellement, la parabole sera alors exinscrite (elle est tangente aux prolongements de deux des côtés du triangle), cependant, on parle tout de même de parabole inscrite.

Parabole tritangente par rapport à un triangle ABC.

Du triangle ABC, on considère un point F de son cercle circonscrit, distinct de A, B et C. Alors la parabole de foyer F et de directrice la droite de Steiner de F est tangente aux trois côtés (étendus) du triangle.

Du triangle ABC, on construit trois triangles isocèles A'BC, B'CA et C'AB. Les triangles ABC et A'B'C' sont homologiques par rapport à une droite. La parabole de Kiepert du triangle est l'enveloppe des axes des homologies. La directrice de la parabole est la droite d'Euler du triangle. Son foyer est le point X(110) dans la nomenclature de Kimberling.

La parabole d'Yff passe par les sommets du triangle d'Yff, qui est le triangle cévian de l'ellipse circonscrite de Steiner du triangle.

Selon la forme du triangle, certaines coniques de l'équation donnée peuvent changer de nature : si le triangle est acutangle, ce sera une ellipse inscrite, mais s'il est obtusangle, elle deviendra une hyperbole dont une des branches est tangente en un point de contact et la deuxième passe par les deux autres.

La conique d'un triangle est l'unique section conique passant par les sommets de son triangle orthique (les bases des hauteurs du triangle de référence). Son point de Brianchon est donc l'orthocentre du triangle. Son centre est au point de Lemoine.

• 
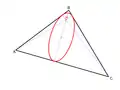  Pour un triangle acutangle, la conique orthique est une ellipse inscrite.
• 
  Pour un triangle obtusangle, la conique orthique est une hyperbole exinscrite.

La conique de Serret (ou de MacBeath) est la conique inscrite de foyers le centre du cercle circonscrit et l'orthocentre du triangle. Son centre est le centre du cercle d'Euler, son point de Brianchon est le conjugué isotomique du centre du cercle circonscrit.

Pour un triangle acutangle, la conique de MacBeath est une ellipse inscrite, aussi dénommée ellipse d'Euler.[6]

Pour un triangle obtusangle, elle est une hyperbole exinscrite.

• 
  Cas du triangle acutangle.
• 
  Cas du triangle obtusangle.