Points de Brocard

Le problème a été posé en 1875 par Henri Brocard comme question dans les Nouvelles Annales de mathématiques[2], et résolu la même année par C. Chadu[3], puis étudié plus longuement par Brocard en 1877[4]. L'appellation "points de Brocard" a été proposée par Joseph Neuberg en 1881[5]. Cependant, la formule de l'angle de Brocard avait déjà été trouvée par August Leopold Crelle en 1816[6]^,[7]^,[8], et C.F.A. Jacobi avait poursuivi l'étude en 1825 [9].

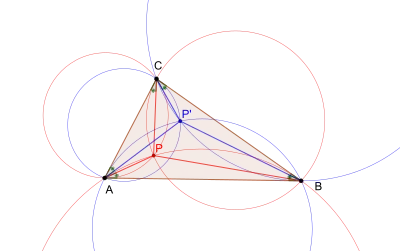
Le premier point de Brocard d'un triangle ABC est le point P tel que les angles ${\displaystyle {\widehat {PAB}},}$ ${\displaystyle {\widehat {PBC}}}$ et ${\displaystyle {\widehat {PCA}}}$ orientés positivement soient égaux.

Le second point de Brocard du triangle est le point P' tel que les angles ${\displaystyle {\widehat {P'BA}},}$ ${\displaystyle {\widehat {P'CB}}}$ et ${\displaystyle {\widehat {P'AC}}}$ orientés positivement soient égaux.

L'existence de ces deux points est une conséquence de la version trigonométrique du théorème de Ceva.

Les angles ${\displaystyle {\widehat {PAB}},}$ ${\displaystyle {\widehat {PBC}},}$ ${\displaystyle {\widehat {PCA}},}$ ${\displaystyle {\widehat {P'BA}},}$ ${\displaystyle {\widehat {P'CB}}}$ et ${\displaystyle {\widehat {P'AC}}}$ sont tous égaux à l'angle de Brocard du triangle, noté ${\displaystyle \omega }$, pouvant être calculé à partir d'une des formules :

• ${\displaystyle \cot \omega =\cot {\widehat {A}}+\cot {\widehat {B}}+\cot {\widehat {C}},}$

• ${\displaystyle \tan \omega ={\frac {4\;S}{a^{2}+b^{2}+c^{2}}},}$
• ${\displaystyle \sin \omega ={\frac {2S}{\sqrt {b^{2}c^{2}+a^{2}c^{2}+a^{2}b^{2}}}},}$
• ${\displaystyle 1/\sin ^{2}\omega =1/\sin ^{2}{\widehat {A}}+1/\sin ^{2}{\widehat {B}}+1/\sin ^{2}{\widehat {C}}}$ [10].

où S désigne l'aire du triangle, a, b, c les longueurs de ses côtés, ${\displaystyle {\widehat {A}},{\widehat {B}},{\widehat {C}}}$ ses angles en A, B, C .

On appelle droite de Brocard l'une quelconque des six droites joignant un sommet du triangle à l'un des points de Brocard.

Elles ne sont pas à confondre avec l'axe de Brocard, qui est la droite reliant le centre du cercle circonscrit au triangle à son point de Lemoine.

Les coordonnées barycentriques du premier et du deuxième point de Brocard sont respectivement : ${\displaystyle \left({\frac {1}{b^{2}}},{\frac {1}{c^{2}}},{\frac {1}{a^{2}}}\right)}$et ${\displaystyle \left({\frac {1}{c^{2}}},{\frac {1}{a^{2}}},{\frac {1}{b^{2}}}\right)}$.

Leurs coordonnées trilinéaires sont respectivemen0 : ${\displaystyle \left({\frac {c}{b}}:{\frac {a}{c}}:{\frac {b}{a}}\right)}$ et ${\displaystyle \left({\frac {b}{c}}:{\frac {c}{a}}:{\frac {a}{b}}\right)}$.

Le milieu des deux points, référencé X(39) dans l'encyclopédie de Kimberling , a pour coordonnées barycentriques :${\displaystyle \left(a^{2}(b^{2}+c^{2}),b^{2}(c^{2}+a^{2}),c^{2}(a^{2}+b^{2})\right)}$.

Les triangles ABC et A(t)B(t)C(t) sont semblables.

Animation de la transformation du triangle A(t)B(t)C(t) pour t variant de 0 à ω.

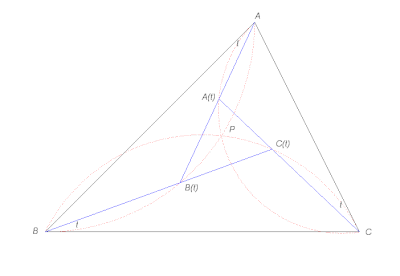
En considérant que le triangle ABC est dans le sens direct, les trois droites isoclines issues respectivement de A, B, C faisant un même angle t avec les droites (AB),(BC),(CA) découpent un triangle A(t)B(t)C(t) qui reste semblable au triangle ABC [10].

Lorsque t est égal à ω, ce triangle se réduit au premier point de Brocart P.

Or, d'après le théorème de l'angle inscrit, le point B(t) décrit le cercle passant par A et B et tangent à (BC) (son centre est donc à l'intersection de la médiatrice de [AB] et de la perpendiculaire à (BC) passant par B), le point C(t) décrit le cercle passant par B et C et tangent à (CA) et le point A(t) décrit le cercle passant par C et A et tangent à (AB). Ceci permet de construire le point P comme intersection de trois cercles.

De façon similaire, le deuxième point de Brocard du triangle ABC s'obtient comme intersection du cercle passant par A et B et tangent à (AC), du cercle passant par B et C et tangent à (BA) et du cercle passant par C et A et tangent à (CB).

Points de Brocard d'un triangle, avec les cercles de construction.

• Les deux points de Brocard sont conjugués isogonaux l'un de l'autre.
• La médiane issue d'un sommet du triangle, la symédiane issue d'un second sommet et une des droites de Brocard issue d'un troisième sommet sont concourantes.

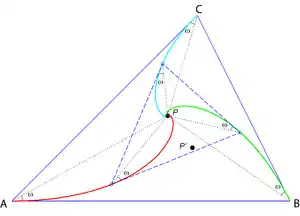
Trois chiens placés initialement aux sommets d'un triangle ABC se poursuivent dans le sens A poursuivant B, poursuivant C, poursuivant A  ; R. K. Miller a déterminé en 1871[10] que le triangle formé par les trois chiens reste semblable à lui-même si et seulement si les vitesses respectives de A,B,C sont  proportionnelles à ${\displaystyle b^{2}c,c^{2}a,a^{2}b}$.

Dans ce cas, le premier point de Brocard du triangle formé par les chiens reste fixe et les chiens se rencontrent simultanément en ce point ; de plus, les courbes décrites sont des spirales logarithmiques[10], par définition tangentielle de ces dernières.

Les coordonnées barycentriques des premier et second points de Brocard invitent à créer un troisième point de Brocard, dont les coordonnées barycentriques sont : ${\displaystyle \left({\frac {1}{a^{2}}},{\frac {1}{b^{2}}},{\frac {1}{c^{2}}}\right)}$.

Ce point porte le numéro X₇₆ dans la nomenclature de Kimberling[11]. Il est situé sur l'hyperbole de Kiepert.