Hyperbole de Kiepert

Dans un triangle non isocèle, l'hyperbole de Kiepert est l'hyperbole équilatère[1] qui passe par les trois sommets et le centre de gravité du triangle[2].

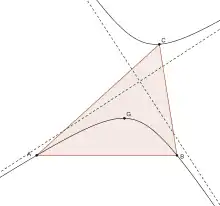
Hyperbole de Kiepert et ses asymptotes

Elle tient son nom du mathématicien Ludwig Kiepert (de) qui la présenta en 1869 dans sa solution du problème de Lemoine (en) (Trouver les sommets d'un triangle connaissant les sommets des trois triangles équilatéraux construits à l’extérieur de celui-ci)[3].

Lieu de points
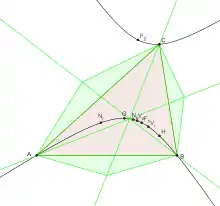
Hyperbole de Kiepert comme lieu de points

Pour un triangle quelconque ABC, on construit trois triangles isocèles directement semblables (ABC'), (BCA') et (CAB'). Si les droites (AA'), (BB') et (CC') ne sont pas parallèles, elles sont alors concourantes en un point M. Dans le cas où le triangle initial n'est pas isocèle, quand l'angle de base des triangles isocèles varie, le point M parcourt l'hyperbole de Kiepert privée d'un point. Si le triangle ABC est isocèle non équilatéral, le point M parcourt l'axe de symétrie du triangle privé d'un point. Si le triangle est équilatéral, le point M est fixe.

Cette propriété permet d'affirmer que les points de Napoléon (Ni et Ne), les points de Vecten (Vi et Ve), les points de Fermat (F1 et F2) et, par limite, l'orthocentre (H) d'un triangle non isocèle sont sur son hyperbole de Kiepert.

Autres points remarquables
Hyperbole de Kiepert - autres points remarquables

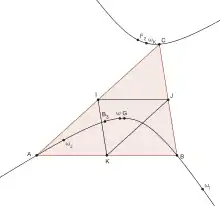
L'hyperbole de Kiepert contient de nombreux autres points remarquables du triangle parmi lesquels le troisième point de Brocard, les centres des cercles inscrit et exinscrits au triangle médian[4],[5] et le point de Tarry (en) (nombre de Kimberling X98)

Asymptote et centre
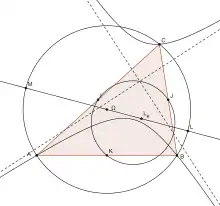
Construction des asymptotes de l'hyperbole de Kiepert du triangle ABC

La droite joignant le point de Lemoine au centre du cercle circonscrit (axe de Brocard) rencontre le cercle en deux points, les droites de Simson de ces deux points sont les asymptotes de l'hyperbole.

Le centre de l'hyperbole, appelé point de Kiepert (nombre de Kimberling X115) se trouve donc sur le cercle d'Euler du triangle[6].

Ce centre est au milieu du segment reliant les deux points de Fermat (nombres de Kimberling X13 et X14). Il est aussi sur le cercle passant par le centre du cercle circonscrit, le centre du cercle d'Euler et le point de Lemoine (nombre de Kimberling X6). Il est aussi sur l'ellipse de Steiner.

Notes et références
  1. Une hyperbole est dite équilatère lorsque ses deux asymptotes sont perpendiculaires.
  2. définition de XTEC - Xarxa Telemàtica Educativa de Catalunya.
  3. Ludwig Kiepert, «Solutions des questions proposées dans les nouvelles annales, question 864», Nouvelles annales de mathématiques, 2e série, tome 8, 1869, pp 38-42
  4. Triangle passant par les milieux des côtés du triangle ABC
  5. Résultat 88 de XTEC - Xarxa Telemàtica Educativa de Catalunya.
  6. (en) Eric W. Weisstein, « Kiepert Hyperbola », sur MathWorld

Voir aussi
  • (en) R. H. Eddy et R. Fritsch, « The Conics of Ludwig Kiepert : A Compehensive Lesson in the Geometry of the Triangle », Mathematics Magazine, vol. 67, no 3,‎ (lire en ligne, consulté le )
  • Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.