Centre du triangle

En géométrie plane, un centre du triangle est un point du plan qui, en un certain sens, peut être vu comme un centre du triangle au même titre que le centre d'un carré ou d'un cercle, c'est-à-dire un point au centre de la figure selon une certaine mesure. Certains de ces points, comme le centre de gravité, le centre du cercle circonscrit, le centre du cercle inscrit et l'orthocentre sont connus depuis la Grèce antique et constructibles simplement.

Chacun de ces centres classiques a la propriété d'être invariant (plus précisément équivariant) par similitudes. En d'autres termes, pour tout triangle et toute similitude (comme une rotation, une symétrie, un agrandissement ou réduction, ou une translation), le centre du triangle transformé est l'image du centre du triangle original par la même transformation. C'est cette invariance qui est la propriété définissante d'un centre du triangle, et exclut donc certains points connus parmi les éléments remarquables comme les points de Brocard qui ne sont pas invariants par symétrie.

Tous les centres d'un triangle équilatéral coïncident en son centre de gravité, mais sont généralement distincts pour un triangle quelconque. Les définitions et propriétés de centaines de ces points sont répertoriés par leur nombre de Kimberling dans l'Encyclopedia of Triangle Centers.

Histoire

Les géomètres de la Grèce antique connaissaient les centres "classiques" d'un triangle, mais ne parlaient pas de centres d'un triangle. Par la suite, d'autres points spéciaux ont été découverts, comme le point de Fermat, le centre du cercle d'Euler, le point de Lemoine, le point de Gergonne ou le point de Feuerbach. Lors du regain d'intérêt pour la géométrie du triangle au cours des années 1980, il a été remarqué que ces points spéciaux partagent certaines propriétés qui forment de nos jours la base de la définition formelle d'un centre d'un triangle[1]^,[2]. Au 1^er septembre 2020, l'Encyclopédie des Centres du Triangle de Clark Kimberling comptait 39 474 entrées annotées[3].

Définition formelle

Une fonction à valeurs réelles $f$ de trois variables réelles $a$ , $b$ , $c$ peut avoir les propriétés suivantes :

Homogénéité :

ll existe une constante

n

telle que, pour tout

t > 0

,

f(ta,tb,tc)=t^{n}f(a,b,c)

.

Bisymétrie entre les deuxième et troisième variables :

f(a,b,c)=f(a,c,b).

Si une fonction $f$ non nulle a ces deux propriétés, on l'appelle fonction centrale[4]. Si $f$ est une fonction centrale et $a$ , $b$ , $c$ sont les longueurs des côtés d'un triangle de référence, alors le point ayant pour coordonnées trilinéaires $(f (a, b, c) : f (b, c, a) : f (c, a, b))$ relativement à ce triangle est un centre du triangle.

La propriété d'homogénéité assure l'invariance par similitude : le centre du triangle image du triangle ABC par une similitude est bien l'image du centre du triangle ABC par cette similitude[5].

La propriété de bisymétrie assure que le centre ne change pas si on permute deux sommets du triangle dans la définition du centre[6].

Il n'est pas nécessaire de donner les trois coordonnées trilinéaires d'un centre du triangle puisque par construction, les seconde et troisième coordonnées se déduisent de la première par permutation circulaire de $a$ , $b$ , $c$ . On parle alors de cyclicité[7]^,[8].

Toute fonction centrale donne naissance à un centre du triangle unique. Cette correspondance n'est cependant pas bijective : différentes fonctions peuvent définir un même centre du triangle. Par exemple, les fonctions $f 1 (a, b, c) = 1/ a$ et $f 2 (a, b, c) = bc$ correspondent toutes deux au centre de gravité. Deux fonctions centrales définissent le même centre si et seulement si leur rapport est une fonction symétrique en $a$ , $b$ , $c$ .

Même si une fonction centrale est bien définie partout, le centre du triangle n'existe pas toujours. Par exemple, soit $f (a, b, c)$ la fonction valant 0 si $a / b$ et $a / c$ sont tous deux rationnels et 1 sinon. Alors pour tout triangle de longueurs entières, le centre associé est de coordonnées trilinéaires 0:0:0 et n'est donc pas défini.

Domaine par défaut

Il n'est pas nécessaire qu'une fonction centrale soit définie sur tout ℝ³. Par exemple, les coordonnées trilinéaires du point X₃₆₅ sont $a 1/2 : b 1/2 : c 1/2$ , ainsi, $a$ , $b$ , $c$ ne peuvent être négatifs. De plus, pour correspondre aux longueurs des côtés d'un triangle, ces quantités doivent vérifier les inégalités triangulaires. Ainsi, en pratique, l'ensemble de définition d'une fonction centrale peut être restreint à l'ensemble des triplets $(a, b, c)$ de ℝ³ vérifiant $a \leq b + c$ , $b \leq c + a$ et $c \leq a + b$ . Cette région T est le domaine de tous les triangles, et le domaine par défaut des fonctions centrales basées sur des triangles.

Autres domaines utiles

Il existe des cas où il peut être utile de restreindre l'analyse à des domaines plus petits que T. Par exemple :

Les centres X₃, X₄, X₂₂, X₂₄, X₄₀ font spécifiquement référence aux triangles acutangles, soit la région de T où

a 2 \leq b 2 + c 2

,

b 2 \leq c 2 + a 2

,

c 2 \leq a 2 + b 2

.

Quand on veut différencier le point de Fermat du point X₁₃, le domaine des triangles dont un angle dépasse $2π/3$ est important, ce qui se traduit par

a 2 > b 2 + bc + c 2

ou

b 2 > c 2 + ca + a 2

ou

c 2 > a 2 + ab + b 2

.

Un domaine bien plus pratique car dense dans T tout en excluant les triangles triviaux (i.e. réduit à un point), dégénérés (i.e. les triangles plats), ou isocèles est l'ensemble des triangles scalènes, obtenu par exclusion des plans $b = c$ , $c = a$ , $a = b$ de T.

Symétrie de domaine

Tout sous-ensemble D ⊆ T n'est pas forcément un domaine conforme. Pour vérifier la bisymétrie, D doit être symétrique par rapport aux plans $b = c$ , $c = a$ , $a = b$ . Pour vérifier la cyclicité, il doit également être invariant pour toute rotation d'angle $2π/3$ autour de la droite $a = b = c$ . Le plus simple de ces domaines admissibles est la droite $(t, t, t)$ qui correspond à l'ensemble des triangles équilatéraux.

Exemples et contre-exemple

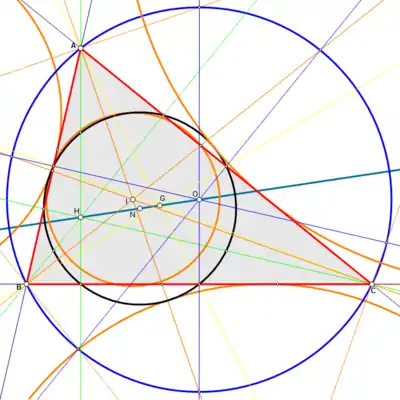
Un triangle ABC avec son centre de gravité G, le centre de son cercle inscrit I, le centre de son cercle circonscrit O, son orthocentre H et le centre de son cercle d'Euler N.

Centre du cercle circonscrit

Le point de concours des médiatrices des côtés d'un triangle ABC est le centre de son cercle circonscrit. Les coordonnées trilinéaires du centre du cercle circonscrit sont

a(b^{2}+c^{2}-a^{2}):b(c^{2}+a^{2}-b^{2}):c(a^{2}+b^{2}-c^{2}).

On pose $f (a, b, c) = a (b 2 + c 2 - a 2)$ . On a alors bien homogénéité et bisymétrie :

f(ta,tb,tc)=(ta)((tb)^{2}+(tc)^{2}-(ta)^{2})=t^{3}\times a(b^{2}+c^{2}-a^{2})=t^{3}f(a,b,c)

f(a,c,b)=a(c^{2}+b^{2}-a^{2})=a(b^{2}+c^{2}-a^{2})=f(a,b,c)

donc $f$ est bien une fonction centrale. Comme le point remarquable du triangle a les mêmes coordonnées trilinéaires que le centre du cercle circonscrit, ce point est bien un centre du triangle.

Premier centre isogonique

On construit, à l'extérieur du triangle ABC, le triangle équilatéral A'BC de base BC et de sommet A'. On construit de façon similaire les triangles équilatéraux AB'C et ABC' le long des deux autres côtés du triangle ABC. Alors les droites (AA'), (BB') et (CC') sont concourantes au premier centre isogonique du triangle (X13). Ses coordonnées trilinéaires sont

\csc \left(A+{\frac {\pi }{3}}\right):\csc \left(B+{\frac {\pi }{3}}\right):\csc \left(C+{\frac {\pi }{3}}\right)

.

où $csc$ est la cosécante (inverse du sinus).

En exprimant $\csc \left(A+{\frac {\pi }{3}}\right)$ à l'aide des longueurs $a$ , $b$ et $c$ , on peut vérifier que l'on obtient bien une fonction centrale donc ce point est un centre du triangle.

Point de Fermat

Soit

f(a,b,c)={\begin{cases}1&\quad {\text{si }}a^{2}>b^{2}+bc+c^{2}&(\mathrm {i.e~} A>2\pi /3),\\0&\quad {\text{si }}b^{2}>c^{2}+ca+a^{2}{\text{ ou }}c^{2}>a^{2}+ab+b^{2}&(\mathrm {i.e.~} B>2\pi /3{\text{ ou }}C>2\pi /3),\\\csc(A+\pi /3)&\quad {\text{sinon }}&(\mathrm {i.e.~aucun~angle~ne~d{\acute {e}}passe~} 2\pi /3).\end{cases}}

Alors $f$ est bisymétrique et homogène donc c'est une fonction centrale. De plus le centre correspondant coïncide avec le sommet d'angle obtus au cas où un des angles dépasse $2π/3$ , et avec le premier centre isogonique sinon. Ainsi, ce centre est le point de Fermat du triangle.

Points de Brocard

Les points de Brocard sont des exemples de points que l'on ne peut pas qualifier de centres du triangle. En effet, les coordonnées trilinéaires du premier point de Brocard sont $c / b : a / c : b / a$ , elles vérifient bien les propriétés d'homogénéité et de cyclicité mais pas la bisymétrie. Le second point de Brocard a pour coordonnées trilinéaires $b / c : c / a : a / b$ et les mêmes remarques peuvent être faites.

Les deux points de Brocard forment une des nombreuses paires bicentriques de points[9], paires de points définies par rapport à un triangle telles que la paire (mais pas chacun pris individuellement) est préservée par des similitudes appliquées au triangle. Plusieurs opérations binaires, comme le milieu et le produit trilinéaire, une fois appliquées aux points de Brocard ou aux autres paires bicentriques, produisent des centres du triangle.

Coordonnées barycentriques

Si un point a pour coordonnées trilinéaires $x : y : z$ , il a pour coordonnées barycentriques $ax : by : cz$ . Il est donc aisé de retrouver les coordonnées barycentriques d'un centre du triangle.

De plus, comme lorsque $f$ est une fonction centrale, $a f$ l'est également, il est possible de définir directement les centres du triangle à l'aide des fonctions centrales et des coordonnées barycentriques.

Quelques centres du triangle connus

Ci-dessous sont présentés quelques centres du triangle connus avec leur noms, leur propriétés caractéristiques et leurs coordonnées trilinéaires

Centres classiques

Nombre de Kimberling associé	Nom	Notation classique	Coordonnées trilinéaires	Description
$X 1$	Centre du cercle inscrit	$I$	$1 : 1 : 1$	Intersection des bissectrices des angles. Centre du cercle inscrit au triangle.
$X 2$	Centre de gravité	$G$	$bc : ca : ab$	Intersection des médianes. Isobarycentre du triangle plan uniforme.
$X 3$	Centre du cercle circonscrit	$O$ ou $Ω$	$cos A : cos B : cos C$	Intersection des médiatrices des côtés. Centre du cercle circonscrit au triangle.
$X 4$	Orthocentre	$H$	$tan A : tan B : tan C$	Intersection des hauteurs du triangle.
$X 5$	Centre du cercle d'Euler	$N$	$cos(B - C) : cos(C - A) : cos(A - B)$	Centre du cercle passant par le milieu de chaque côté, les pieds des hauteurs et les milieux des segments entre l'orthocentre et chaque sommet.
$X 6$	Point de Lemoine	$K$	$a : b : c$	Intersection des symédianes (droites symétriques des médianes par rapport aux bissectrices correspondantes).
$X 7$	Point de Gergonne	$G e$	$bc /(b + c - a) : ca /(c + a - b) : ab /(a + b - c)$	Intersection des droites reliant les sommets et les points de contact du cercle inscrit avec le côté opposé.
$X 8$	Point de Nagel	$N a$	$(b + c - a)/ a : (c + a - b)/ b : (a + b - c)/ c$	Intersection reliant les sommets et les points de contact des cercle exinscrits au côté opposé.
$X 9$	Mittenpunkt	$M$	$b + c - a : c + a - b : a + b - c$	Plusieurs définitions.
$X 10$	Centre du cercle de Spieker	$S p$	$bc (b + c) : ca (c + a) : ab (a + b)$	Centre du cercle inscrit au triangle médian. Isobarycentre des côtés du triangle.
$X 11$	Point de Feuerbach	$F$	$1 - cos(B - C) : 1 - cos(C - A) : 1 - cos(A - B)$	Point de tangence entre le cercle d'Euler et le cercle inscrit.
$X 13$	Point de Fermat (*)	$X$	$csc(A + π/3) : csc(B + π/3) : csc(C + π/3)$	Point tel que la somme des distances aux sommets soit la plus petite.
$X 15$ , $X 16$	Points isodynamiques	$S$ $S'$	$sin(A + π/3) : sin(B + π/3) : sin(C + π/3) sin(A - π/3) : sin(B - π/3) : sin(C - π/3)$	Centres des inversions qui transforment le triangle en un triangle équilatéral.
$X 17$ , $X 18$	Points de Napoléon	$N$ $N'$	$sec(A - π/3) : sec(B - π/3) : sec(C - π/3) sec(A + π/3) : sec(B + π/3) : sec(C + π/3)$	Intersection des droites reliant les sommets du triangle au sommet d'un triangle équilatéral pointant vers l'extérieur (pour le 1^er point) ou à l'intérieur (pour le 2^e point), avec pour base le côté opposé.
$X 99$	Point de Steiner	$S$	$bc /(b 2 - c 2) : ca /(c 2 - a 2) : ab /(a 2 - b 2)$	Plusieurs définitions.

(*) : il s'agit plus précisément du premier centre isogonique, confondu avec le point de Fermat pour des angles aux sommets n’excédant pas $2π/3$ .

Centres récents

Les centres notables découverts plus récemment n'ont pas de notation courante. Seule la première coordonnée trilinéaire $f (a, b, c)$ sera spécifiée, les deux autres étant obtenues par cyclicité des coordonnées trilinéaires.

Numéro de Kimberling	Nom	Fonction centrale $f (a, b, c)$	Description	Année de découverte
$X 21$	Point de Schiffler	$1/(cos B + cos C)$		1985
$X 22$	Point d'Exeter	$a (b 4 + c 4 - a 4)$	Point de concurrence des droites passant par les points de concurrence entre les médianes et le cercle circonscrit au triangle et les tangentes au cercle circonscrit au sommet du triangle.	1986
$X 111$	Point de Parry (en)	$a /(2 a 2 - b 2 - c 2)$	Centre du cercle de Parry (cercle passant par le centre de gravité et les deux points isodynamiques)	début des années 1990
$X 173$	Point des isocéliseurs congruents (en)	$tan(A /2) + sec(A /2)$		1989
$X 174$	Centre de congruence d'Yff (en)	$sec(A /2)$		1987
$X 175$	Point isopérimétrique	$- 1 + sec(A /2) cos(B /2) cos(C /2)$		1985
$X 179$	Premier point d'Ajima-Malfatti	$sec 4 (A /4)$
$X 181$	Point d'Apollonius	$a (b + c) 2 /(b + c - a)$		1987
$X 192$	Point des parallèliennes égales (en)	$bc (ca + ab - bc)$	Point d'intersection des trois segments intérieurs au triangle, parallèles à un côté, dont les extrémités sont sur les deux autres côtés, et tous trois égaux.	1961
$X 356$	Centre de Morley	$cos(A /3) + 2 cos(B /3) cos(C /3)$	Centre des cercles circonscrits aux triangles de Morley (triangles équilatéraux formés par les intersections des trisectrices aux sommets)
$X 360$	Point zéro de Hofstadter	$A / a$		1992

Classes générales de centres du triangle

Centres de Kimberling

En honneur de Clark Kimberling, créateur de l'encyclopédie en ligne qui répertorie et classe plus de 32 000 centres du triangle, ceux-ci sont appelés généralement centres de Kimberling[10].

Centre polynomial de triangle

Un centre du triangle est dit polynomial si ses coordonnées trilinéaires peuvent être exprimées comme des polynômes en $a$ , $b$ et $c$ .

Centre régulier du triangle

Un centre du triangle est dit régulier si ses coordonnées trilinéaires peuvent être exprimées comme des polynômes en $a$ , $b$ et $c$ , et son aire $S$ .

Centre majeur du triangle

Un centre du triangle est dit majeur si ses coordonnées trilinéaires peuvent être exprimées sous la forme $f (A) : f (B) : f (C)$ où $f$ ne dépend que de l'angle A et non des deux autres angles ou des longueurs des côtés[11].

Centre transcendant du triangle

Un centre du triangle est dit transcendant si ses coordonnées trilinéaires ne peuvent être exprimées par des fonctions algébriques de $a$ , $b$ et $c$ .

Cas particuliers

Triangles isocèles et équilatéraux

Soit $f$ une fonction centrale.Si deux côtés du triangle sont égaux (par exemple $a = b)$ , alors

f (a, b, c) = f (b, a, c)

car

a = b

f (a, b, c) = f (b, c, a)

par la bisymétrie

donc deux coordonnées du centre du triangle associé sont toujours égales. Ainsi, tous les centres du triangle sont alignés sur son axe de symétrie. Pour un triangle équilatéral, ils sont donc confondus avec son centre de gravité. Ainsi, comme un cercle, un triangle équilatéral a un centre unique.

Centres des cercles exinscrits

Soit

f(a,b,c)={\begin{cases}-1&\quad {\text{si }}a\geq b{\text{ et }}a\geq c,\\\;\;\;1&\quad {\text{sinon}}.\end{cases}}

On peut vérifier qu'il s'agit d'une fonction centrale et (pourvu que le triangle est scalène) le centre correspondant est le centre du cercle exinscrit opposé au plus grand angle au sommet. Les deux autres centres des cercles exinscrits peuvent être définies par des fonctions similaires. Cependant, comme vu plus haut, seul un des centres des cercles exinscrits d'un triangle isocèle et aucun pour un triangle équilatéral peuvent être vu comme un centre du triangle.

Fonctions bi-antisymétriques

Une fonction $f$ est bi-antisymétrique si $f (a, b, c) = - f (a, c, b)$ pour tous $a, b, c$ . Une telle fonction, de plus non nulle et homogène, existe, on peut facilement voir que la fonction $(a, b, c) \to f (a, b, c) 2 f (b, c, a) f (c, a, b)$ est une fonction centrale. Le centre correspondant a pour coordonnées $f (a, b, c) : f (b, c, a) : f (c, a, b)$ . En prenant en compte ceci, la définition d'un centre du triangle est parfois modifiée pour inclure les fonctions non nulles homogènes bi-antisymétriques.

Centres nouveaux et anciens

Toute fonction centrale $f$ peut être normalisée en la multipliant par une fonction symétrique de $a$ , $b$ , $c$ de sorte que $n = 0$ . Une fonction centrale normalisée a le même centre du triangle que l'originale, et une propriété plus forte sur l'homogénéité $f (ta, tb, tc) = f (a, b, c)$ pour tout $t > 0$ et tout triplet $(a, b, c)$ . Réunis avec la fonction nulle, les fonctions centrales normalisées forment une algèbre munie de l'addition, la soustraction et la multiplication. On a ainsi un moyen simple de créer de nouveaux centres du triangle. Toutefois, deux fonctions centrales normalisées vont souvent définir un même centre du triangle, par exemple $f$ et $(a + b + c) 3 / abc f$ .

Centres sans intérêt

On suppose $a, b, c$ trois variables réelles et soient $α, β, γ$ trois constantes réelles. On considère

f(a,b,c)={\begin{cases}\alpha &\quad {\text{ si }}\min(a,b,c)=a,\\\gamma &\quad {\text{ si }}\max(a,b,c)=a,\\\beta &\quad \;{\text{sinon}}.\end{cases}}

Alors $f$ est une fonction centrale et $α : β : γ$ est le centre correspondant dès que les côtés du triangle de référence sont notés de sorte que $a < b < c$ . Ainsi, tout point eut potentiellement pu être un centre du triangle. Cependant la grande majorité de ces centres n'ont que peu d'intérêt, au même titre que la plupart des fonctions continues n'ont que peu d'intérêt. L'Encyclopedia of Triangle Centers se concentre sur ceux qui sont intéressants et continue de s'agrandir.

Systèmes binaires

Il existe d'autres paires de centres que le point de Fermat et le premier centre isogonique. On en trouve un autre entre $X 3$ et le centre du cercle inscrit au triangle tangentiel. En effet, on considère la fonction centrale suivante :

f(a,b,c)={\begin{cases}\cos(A)\quad \;\quad \;\quad \;\quad \;\quad \;\quad \;\,\,{\text{pour un triangle acutangle}},\\\cos(A)+\sec(B)\sec(C)\quad {\text{si l'angle en }}A{\text{ est obtus}},\\\cos(A)-\sec(A)\quad \;\quad \;\quad \;\,{\text{si l'un des angles en }}B{\text{ ou }}C{\text{ est obtus}}.\end{cases}}

Pour le centre correspondant, on a quatre possibilités distinctes :

$cos(A) : cos(B) : cos(C)$ pour un triangle de référence acutangle (on retrouve ici le centre du cercle circonscrit) ;
$[cos(A) + sec(B)sec(C)] : [cos(B) - sec(B)] : [cos(C) - sec(C)]$ si l'angle en A est obtus ;
$[cos(A) - sec(A)] : [cos(B) + sec(C)sec(A)] : [cos(C) - sec(C)]$ si l'angle en B est obtus ;
$[cos(A) - sec(A)] : [cos(B) - sec(B)] : [cos(C) + sec(A)sec(B)]$ si l'angle en C est obtus.

Le calcul montre que dans tous les cas, ces coordonnées trilinéaires sont celles du centre au cercle inscrit au triangle tangentiel, mais peuvent correspondre également au centre du cercle circonscrit.

Géométries non-euclidiennes et autres

L'étude des centres du triangle renvoie traditionnellement à la géométrie euclidienne, mais les centres du triangle peuvent être recherchés dans une géométrie non-euclidienne[12]. Les centres du triangle dans la géométrie sphérique peuvent être définis par la trigonométrie sphérique[13]. Les centres du triangle qui ont la même forme pour les géométries euclidienne et hyperbolique peut être exprimés par gyrotrigonométrie[14]^,[15]^,[16]. En géométrie non euclidienne, l'hypothèse que la somme des angles intérieurs du triangle valant 180° doit être écartée.

Les centres des tétraèdres ou de simplexes de dimension supérieure peuvent aussi être définies, par analogie avec les triangle en dimension deux[16].

Voir aussi

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Triangle center » (voir la liste des auteurs).

(en) Clark Kimberling, « Triangle centers » (consulté le 23 mai 2009) : « Unlike squares and circles, triangles have many centers. The ancient Greeks found four: incenter, centroid, circumcenter, and orthocenter. A fifth center, found much later, is the Fermat point. Thereafter, points now called nine-point center, symmedian point, Gergonne point, and Feuerbach point, to name a few, were added to the literature. In the 1980s, it was noticed that these special points share some general properties that now form the basis for a formal definition of triangle center »
(en) Clark Kimberling, « Central Points and Central Lines in the Plane of a Triangle », Mathematics Magazine, vol. 67, n^o 3,‎ juin 1994, p. 163–187 (DOI 10.2307/2690608, JSTOR 2690608)
(en) Clark Kimberling, « This is PART 20: Centers X(38001) - X(40000) », sur Encyclopedia of Triangle Centers
François Lavallou, « cubiques du triangle », Hors Série tangente 74 - Courbes et trajectoires,‎ avril 2020, p. 36 (lire en ligne )
(en) Clark Kimberling, « Triangle centers as functions », The Rocky Mountain Journal of Mathematics, vol. 23, n^o 4,‎ 1993, p. 1269-1286 (lire en ligne), p. 1274
Kimberling 1993, p. 1273.
Eric W Weisstein, « Triangle Center », sur MathWorld–A Wolfram Web Resource. (consulté le 25 mai 2009)
Eric W Weisstein, « Triangle Center Function », sur MathWorld–A Wolfram Web Resource. (consulté le 1^er juillet 2009)
(en) « Bicentric Pairs of Points », sur Encyclopedia of Triangle Centers
Eric W Weisstein, « Kimberling Center », sur MathWorld–A Wolfram Web Resource. (consulté le 25 mai 2009)
Eric W Weisstein, « Major Triangle Center », sur MathWorld–A Wolfram Web Resource (consulté le 25 mai 2009)
(en) Robert A. Russell « Non-Euclidean Triangle Centers », 2019.
(en) Rob Johnson, « Spherical Trigonometry », sur West Hills Institute of Mathematics
(en) Abraham A. Ungar, « Hyperbolic Barycentric Coordinates », The Australian Journal of Mathematical Analysis and Applications, vol. 6, n^o 1,‎ 2009, p. 1-35 (lire en ligne)
(en) Abraham A. Ungar, « Hyperbolic Triangle Centers: The Special Relativistic Approach », Springer Science & Business Media,‎ 2010 (lire en ligne)
(en) Abraham Ungar, Barycentric Calculus In Euclidean And Hyperbolic Geometry : A Comparative Introduction, World Scientific, 2010 (lire en ligne)

Liens externes

(en) Manfred Evers, On Centers and Central Lines of Triangles in the Elliptic Plane
(en) Manfred Evers, On the geometry of a triangle in the elliptic and in the extended hyperbolic plane
(en) Clark Kimberling, Triangle Centers sur le site de l'Université d'Evansville
(en) Ed Pegg, Triangle Centers in the 2D, 3D, Spherical and Hyperbolic sur Wolfram Research.
(en) Paul Yiu, A Tour of Triangle Geometry sur le site de la Florida Atlantic University.

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Clark Kimberling, « Triangle centers » (consulté le 23 mai 2009) : « Unlike squares and circles, triangles have many centers. The ancient Greeks found four: incenter, centroid, circumcenter, and orthocenter. A fifth center, found much later, is the Fermat point. Thereafter, points now called nine-point center, symmedian point, Gergonne point, and Feuerbach point, to name a few, were added to the literature. In the 1980s, it was noticed that these special points share some general properties that now form the basis for a formal definition of triangle center »

[2] (en) Clark Kimberling, « Central Points and Central Lines in the Plane of a Triangle », Mathematics Magazine, vol. 67, n^o 3,‎ juin 1994, p. 163–187 (DOI 10.2307/2690608, JSTOR 2690608)

[3] (en) Clark Kimberling, « This is PART 20: Centers X(38001) - X(40000) », sur Encyclopedia of Triangle Centers

[4] François Lavallou, « cubiques du triangle », Hors Série tangente 74 - Courbes et trajectoires,‎ avril 2020, p. 36 (lire en ligne )

[5] (en) Clark Kimberling, « Triangle centers as functions », The Rocky Mountain Journal of Mathematics, vol. 23, n^o 4,‎ 1993, p. 1269-1286 (lire en ligne), p. 1274

[Kimberling19931273-6] Kimberling 1993, p. 1273.

[wolf1-7] Eric W Weisstein, « Triangle Center », sur MathWorld–A Wolfram Web Resource. (consulté le 25 mai 2009)

[8] Eric W Weisstein, « Triangle Center Function », sur MathWorld–A Wolfram Web Resource. (consulté le 1^er juillet 2009)

[9] (en) « Bicentric Pairs of Points », sur Encyclopedia of Triangle Centers

[10] Eric W Weisstein, « Kimberling Center », sur MathWorld–A Wolfram Web Resource. (consulté le 25 mai 2009)

[11] Eric W Weisstein, « Major Triangle Center », sur MathWorld–A Wolfram Web Resource (consulté le 25 mai 2009)

[12] (en) Robert A. Russell « Non-Euclidean Triangle Centers », 2019.

[13] (en) Rob Johnson, « Spherical Trigonometry », sur West Hills Institute of Mathematics

[14] (en) Abraham A. Ungar, « Hyperbolic Barycentric Coordinates », The Australian Journal of Mathematical Analysis and Applications, vol. 6, n^o 1,‎ 2009, p. 1-35 (lire en ligne)

[15] (en) Abraham A. Ungar, « Hyperbolic Triangle Centers: The Special Relativistic Approach », Springer Science & Business Media,‎ 2010 (lire en ligne)

[barycalc-16] (en) Abraham Ungar, Barycentric Calculus In Euclidean And Hyperbolic Geometry : A Comparative Introduction, World Scientific, 2010 (lire en ligne)