Plan hippodamien
Un plan hippodamien ou hippodaméen (dit aussi milésien, en damier, en échiquier, quadrillé, ou orthogonal), est, en urbanisme, un type d'organisation de la ville dans lequel les rues sont rectilignes et se croisent en angle droit, créant des îlots de forme carrée ou rectangulaire.


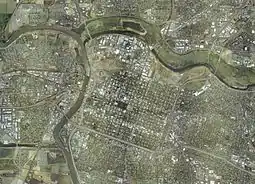
Ce plan est largement repris par les Grecs de l'Antiquité pour leurs colonies, et ensuite par les Romains qui en font la base des villes établies à la suite de l'établissement de l'Empire à travers toute l'Europe[réf. souhaitée].
Il ne doit pas être confondu avec le plan lui aussi orthogonal établi pour les bastides dans le Sud-ouest de la France.
Origine
L'adjectif hippodamien est issu du nom d'Hippodamos, architecte grec considéré comme l'un des pères de l'urbanisme et dont les plans d'aménagement étaient caractérisés par des rues rectilignes et larges qui se croisaient à angle droit. Cependant, il n'est pas l'inventeur de ce plan, comme en témoigne la colonie sumérienne d'Habuba Kabira construite à la fin du IVe millénaire av. J.-C., sur un plan préconçu en damier[1] ou la ville étrusque de Misano au VIe siècle av. J.-C.[2]. Le qualificatif milésien provient de la ville de naissance d'Hippodamos, Milet.
L'appellation en damier ou en échiquier fait référence au plateau du jeu de dames ou d'échecs, dont les cases forment un motif identique.
Présentation

Pour les Romains, ce plan traduit la volonté des fondateurs de la ville d'organiser rationnellement le territoire en se basant sur le cardo maximus et le decumanus à la manière de la centuriation romaine, elle-même inspirée du bornage étrusque. Avec un tel plan, il est en théorie possible de calculer la distance entre deux blocs, quel que soit le quartier où l'on se trouve, avec l'algorithme de la « distance de Manhattan ».
Cependant, malgré sa simplicité apparente, ce type de plan présente des inconvénients : il rallonge les temps de trajet (sauf si on ouvre des « diagonales » pour circuler comme à Barcelone, ou Broadway à Manhattan) et fait fi de la topographie. Mais l'inconvénient de la forte pente des rues de San Francisco, qui en est l'exemple le plus célèbre, constitue pourtant un des charmes de cette ville.
Exemples
Ont un plan quadrillé :
- les villes fondées par les Grecs à l’époque classique et à l'époque hellénistique, puis par les Romains, pendant l'Antiquité ;
- l’Etrusco ritu du bornage étrusque, pour la fondation des villes, imposait un tel plan, même si la configuration des lieux d'implantation n'a pas toujours permis de le respecter.
- les villes chinoises, comme Pékin, Xi'an ;
- certaines villes japonaises comme l'ancienne capitale, Heiankyo (devenue Kyōto) et la ville moderne de Sapporo ;
- beaucoup de villes européennes médiévales (par exemple les bastides, villes nouvelles du Sud-Ouest français) ou modernes (Richelieu et Bussy-Saint-Georges en France, La Chaux-de-Fonds en Suisse, places fortes, villes nouvelles) ou encore des quartiers tels que la ville-neuve de Nancy, le centre-ville de Saint-Étienne (depuis la Révolution et les plans de l'architecte Pierre-Antoine Dalgabio) ou la New Town d'Édimbourg ;
- de nombreuses villes au Canada comme Montréal (extrémités Ouest et Est d'une même voie à travers la ville), aux États-Unis comme New York (où les axes de circulation sont appelés rues ou avenues selon leur orientation) ;
- des villes baroques, comme Turin et Mannheim ;
- les villes fondées par les Européens, à l'époque de la colonisation, telles Kinshasa ou New Delhi, et les villes fondées depuis leur indépendance dans les « pays neufs » ;
- les villes reconstruites après une catastrophe, tel le quartier de la Baixa à Lisbonne ou Reggio de Calabre;
- les centres-villes français bombardés et reconstruits après la Seconde Guerre mondiale : Le Havre (voir l'article détaillé Centre-ville reconstruit du Havre), Brest, les quartiers est de Nice, etc. Plusieurs villes du nord de la Scandinavie, telles Alta en Norvège ou Rovaniemi en Finlande, ont ainsi également été reconstruites après 1945 ;
- des villes conçues au XXe siècle comme dans les polders néerlandais, avec Haarlemmermeer, ou la ville nouvelle de Val-de-Reuil construite dans les années 1970 ;
- de nombreuses villes d'Amérique Latine construites par les colons espagnols comme Bogota. Ces plans d'urbanisme présentaient l'avantage d'une meilleure circulation de l'air supposée réduire les risques d'épidémies, conformément aux enseignements de Galien. Cela présente également des facilités pour faire sonner la charge de cavalerie et faire tirer aux arquebuses dans l'éventualité d'une rébellion indienne.
- Barcelone, pour l’agrandissement de l'Eixample selon le plan Cerdà de 1860.
Galerie d'images
 Plan de Pompéi.
Plan de Pompéi. Sapporo de nuit.
Sapporo de nuit. Maquette de Heiankyo.
Maquette de Heiankyo. Campus de l'Université de San Francisco.
Campus de l'Université de San Francisco.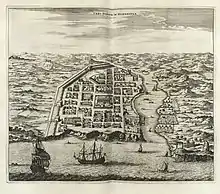 Plan de Saint-Domingue en 1671.
Plan de Saint-Domingue en 1671.

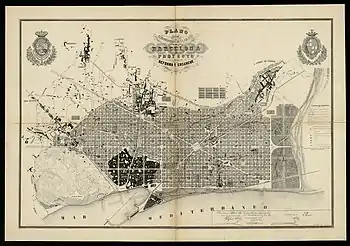 Plan Cerda de 1859 pour Barcelone.
Plan Cerda de 1859 pour Barcelone. Quartier de Barcelone.
Quartier de Barcelone. Vue aérienne de l'Eixample, Barcelone - l'avenue Diagonale coupe le plan en damier.
Vue aérienne de l'Eixample, Barcelone - l'avenue Diagonale coupe le plan en damier. Rue d'Indianapolis.
Rue d'Indianapolis.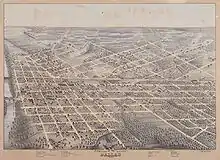 Plan de Dallas en 1872.
Plan de Dallas en 1872.




 Plan de Québec en 1906.
Plan de Québec en 1906.
 Plan de Manhattan en 1879.
Plan de Manhattan en 1879. Plan du Pirée en 1908.
Plan du Pirée en 1908. Plan de Memphis en 1870.
Plan de Memphis en 1870. Plan de Saint-Étienne et de son centre organisé selon un quadrillage autour de la Grand'Rue.
Plan de Saint-Étienne et de son centre organisé selon un quadrillage autour de la Grand'Rue.
Articles connexes
- Commissioners' Plan de 1811 (New York, USA)
- Îlot urbain
- Plan radioconcentrique
Notes et références
- Corinne Castel, « La première ville n’existe pas. Les premières villes ne sont pas toutes sumériennes… (2ème partie) », blog ArchéOrient, 26 juin 2015.
- Catherine Virlouvet (dir.) et Stéphane Bourdin, Rome, naissance d'un empire : De Romulus à Pompée 753-70 av. J.-C, Paris, Éditions Belin, coll. « Mondes anciens », , 796 p. (ISBN 978-2-7011-6495-3), chap. 4 (« Rome et l'Italie »), p. 152.
- Portail de l’architecture et de l’urbanisme
- Portail de la géographie