Transformation par polaires réciproques
En mathématiques, et plus précisément en géométrie, la transformation par polaires réciproques est une transformation associant à une courbe une autre courbe construite à l'aide des droites tangentes à la première. La courbe image s'appelle la courbe duale de la courbe de départ.
Pour les articles homonymes, voir Polaire.
Définition
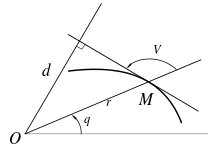
On considère une courbe plane Γ0. La courbe polaire au point M0 (x0(t), y0(t)) de Γ0 par rapport à un cercle (C) (ou de cercle directeur (C)) est l'enveloppe des polaires des points de Γ0 par rapport à (C) ; c'est donc l'ensemble des pôles des tangentes à Γ0 par rapport à (C).
- Equations
La polaire par rapport au cercle de centre O et de rayon r et un point M0 (x0, y0) est la droite des points M (x , y) tels que x0x + y0y = r2.
Si M0(x0(t), y0(t)) est le point courant d'une courbe Γ0, le point courant M(x(t), y(t)) de la polaire de Γ0 est défini, en coordonnées cartésiennes, par
soit, en coordonnées complexes :
La « polarisation » échange donc les notions de point d'une courbe et de tangente à la courbe.
Polaire d'une conique
La polaire d'une conique par rapport à un cercle centré en un foyer de la conique est un cercle centré au pôle de la directrice.
Propriétés
- La transformation par polaires réciproques est une involution : la polaire d'une polaire par rapport au même cercle est égale à la courbe de départ.
- La polaire n'est pas à confondre avec la courbe inverse. D'ailleurs, l'inverse de la polaire par rapport au même cercle est la courbe podaire.
- La polaire d'une courbe algébrique est une courbe algébrique dont le degré est égal à la classe de la courbe de départ (c'est-à-dire le degré de l'équation tangentielle).
Exemples
| Courbe de départ | Position du centre du cercle directeur par rapport à la courbe de départ | Position du centre du cercle directeur par rapport à la polaire | Polaire |
|---|---|---|---|
| Droite (polaire du point) | Hors de la droite | Différent du point | Point (pôle de la droite) |
| Conique[1] | Conique | ||
| Foyer de la conique | Cercle | ||
| À l'intérieur de la conique (i.e. dans une région contenant un foyer) | Ellipse | ||
| À l'extérieur de la conique | Hyperbole | ||
| Sur la conique | Parabole | ||
| Cardioïde | Point de rebroussement | Foyer au 8/9e du segment joignant le point double au sommet | Cubique de Tschirnhausen |
| Centre du cercle conchoïdal | Foyer | Trisectrice de Maclaurin | |
| Deltoïde | Centre | Sommet | Cubique duplicatrice |
| Astroïde | Centre | Centre | Cruciforme |
| Cycloïde à centre | Centre | Centre | Épi |
| Spirale sinusoïdale de paramètre α | Centre | Centre | Spirale sinusoïdale de paramètre -αα+1 |
Extensions aux surfaces tridimensionnelles
Le concept de polaire réciproque peut être étendu aux surfaces dans l'espace ; la surface transformée devient alors une autre surface[2],[3].
Voir aussi
Références
- Jacques Lenthéric, « Théorie générale des polaires réciproques planes », Nouvelles annales de mathématiques, 1re série, vol. 8, , p. 252-266
- L. Quantin de la Roëre, « Développables formées avec les normales d'une quadrique », Nouvelles annales de mathématiques, 5e série, vol. 1, , p. 153-159 (lire en ligne)
- Pierre Papillon, « Sur les surfaces polaires réciproques des conoïdes », Annales de la faculté des sciences de Toulouse, 3e série, vol. 25, , p. 239-256 (lire en ligne)
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, (ISBN 978-2-91-635208-4) ;
- Bruno Ingrao, Coniques projectives, affines et métriques, Calvage & Mounet, (ISBN 978-2916352121).
- Portail de la géométrie