Réaction en chaîne (nucléaire)
En physique nucléaire, une réaction en chaîne se produit lorsqu'un neutron cause la fission d'un noyau atomique fissile produisant un plus grand nombre de neutrons, qui à leur tour causent d'autres fissions, permettant de poursuivre cette réaction.
Pour les articles homonymes, voir Réaction en chaîne.

1. Un atome d'uranium 235 absorbe un neutron et se divise en deux nouveaux atomes (produits de fission), relâchant trois nouveaux neutrons et de l'énergie de liaison.
2. L'un des neutrons est absorbé par un atome d'uranium 238 et ne continue pas la réaction, un autre neutron est simplement perdu. Cependant, un neutron entre en collision avec un atome d'uranium 235, qui se divise et relâche deux neutrons et de l'énergie de liaison.
3. Ces deux neutrons entrent en collision avec des atomes d'uranium 235, qui se divisent et relâchent de un à trois neutrons, qui peuvent encore entretenir la réaction.
Une réaction en chaîne non contrôlée se produisant avec une quantité suffisamment importante de combustible fissile (masse critique) peut mener à une explosion : c'est le principe d'une bombe atomique. La réaction en chaîne peut aussi être contrôlée et utilisée dans un réacteur nucléaire pour produire de l'énergie thermique, elle même susceptible d'être utilisée pour produire de l'électricité : c'est le principe de fonctionnement des centrales nucléaires.
Histoire
Le concept a été développé par le physicien hongro-américain Leó Szilárd en 1933, qui déposa un brevet l'année suivante[1]. Leo Szilárd essaya de créer une réaction en chaîne avec du béryllium et de l'indium en 1936 mais sans succès.
Une estimation de cette masse critique est publiée en 1939 par Francis Perrin dans une note du à l’Académie des sciences, dans laquelle il introduit le terme de « masse critique » et l´estime à 40 tonnes d’oxyde d’uranium[2],[3].
Le , Enrico Fermi et Leó Szilárd réalisent à l'université de Chicago la première réaction en chaîne, fondée sur la fission nucléaire de noyaux atomiques fissiles, dans le cadre du projet Manhattan. Chicago Pile-1 (CP-1), la première pile atomique au monde, emploie 36 tonnes d'oxyde d'uranium, 6 tonnes d'uranium et près de 400 tonnes de graphite comme modérateur. À la suite de leurs expériences, Fermi et Szilárd déposent plusieurs brevets en 1944 et 1945[4].
En , un site naturel ayant abrité une réaction en chaîne spontanée auto-entretenue sous la surface de la Terre est découvert et caractérisé par Francis Perrin, alors haut-commissaire au CEA, à Oklo, en Afrique. C'est le seul réacteur nucléaire naturel connu au monde à ce jour[5].
Facteur de multiplication des neutrons
Lors d'une réaction de fission nucléaire, l'absorption d'un neutron par un noyau fissile permet la libération de plusieurs neutrons. Chaque neutron émis peut à son tour casser un autre noyau fissile et la réaction se poursuit ainsi d'elle-même. Cette réaction en chaîne n'a lieu que si au moins un neutron émis lors d'une fission provoque une nouvelle fission.
Voici trois équations de fissions, montrant les résultats moyens attendus du bombardement d'un noyau fissile par un neutron:
- 238U + neutron = 239U
- 235U + neutron = produits de fission + 2,47 neutrons + 193,2 MeV
- 239Pu + neutron = produits de fission + 2,91 neutrons + 198,6 MeV
Ces équations ne tiennent pas compte des 9,6 et 8,6 MeV pour les neutrinos inutiles et quasiment indétectables.
Dans un milieu réactif, la vitesse à laquelle se déroule cette réaction en chaîne est mesurée par le facteur de multiplication. Le facteur de multiplication (noté k) est le nombre moyen de neutrons émis par une fission qui engendrent une nouvelle fission nucléaire, dans un milieu réactif (on dit aussi milieu multiplicateur) donné. Les autres neutrons issus de la fission sont absorbés sans provoquer de fission nucléaire, ou s'échappent du système.
La valeur de k gouverne l'évolution d'une réaction en chaîne :
- Si k<1 (situation sous-critique) : le système ne peut pas entretenir une réaction en chaîne, et toute chaîne finit par s'éteindre. Pour chaque fission qui apparaît dans le système, il y a en moyenne 1/(1 − k) fissions induites.
- Si k = 1 (situation critique) : chaque fission engendre en moyenne une autre fission, ce qui conduit à un niveau de réaction (et de puissance) constant. Les réacteurs nucléaires sont pilotés pour opèrer à k=1.
- k>1 (situation super-critique) : pour chaque fission qui apparaît dans la matière fissible, il y a en moyenne k fissions à la génération suivante. Le nombre de fissions croît exponentiellement, suivant la formule , où t est le temps. Les armes nucléaires sont conçues pour fonctionner dans cet état et provoquer une explosion.
Réactivité d'un milieu
La réactivité d'un système nucléaire dépend à la fois de la nature des matériaux présents (densité de matières fissiles, présence de modérateur...) et de sa géométrie (taille de l'assemblage, présence de réflecteurs neutroniques...) ; un assemblage est en règle générale d'autant moins réactif qu'il est petit, parce que les neutrons produits dans la partie réactive se perdent au-delà de sa frontière dans un milieu moins réactif.
Pour cette raison, on calcule souvent d'abord le facteur de multiplication kinfini d'un milieu supposé infini, qui est le maximum qui puisse être atteint par un milieu de nature donnée, et dans un deuxième temps on calcule la taille effective qu'il faut lui donner pour avoir une réactivité positive, compte tenu des conditions aux limites de l'assemblage (fuites et présence d'éventuels réflecteurs).
La réactivité ρ (exprimée en pcm, pour cent mille) est une grandeur permettant de mesurer l'écart d'un cœur (ou d'un assemblage critique) par rapport à la criticité. La réactivité est calculée à partir du keff via l'une ou l'autre des formules ci-dessous :
- =
Vitesse des réactions en chaîne
Durée de vie des neutrons directs
La durée de vie des neutrons directs, l, est le délai moyen entre une émission d'un neutron et soit leur absorption par le système, ou leur sortie des limites du système. Le terme « durée de vie » est utilisé parce que l'émission d'un neutron est considérée comme sa « naissance », et son absorption ultérieure est assimilable à une « mort ».
Le temps moyen entre générations, Λ, est le temps moyen qui sépare l'émission d'un neutron de sa capture par un noyau fissile, résultant en une nouvelle fission. Ce temps moyen est différent de la durée de vie du neutron émis, parce que le temps moyen entre neutrons n'inclut que les neutrons qui induisent une nouvelle fission (et ne comprend pas ceux qui sont perdus par ailleurs). Ces deux durées de vie sont reliées par la formule suivante :
Dans cette formule, k est le facteur (multiplicatif) d'efficacité neutronique.
Pour des réacteurs à neutrons thermiques (dont la vitesse est relativement lente), la durée de vie typique d'un neutron est de l'ordre de 10−4 secondes ; pour des réacteurs à neutrons rapides, cette durée de vie est de l'ordre de 10−7 secondes. Ces durées extrêmement courtes signifient qu'en une seconde, il peut y avoir de 10 000 à 10 000 000 générations de neutrons.
Ce nombre de générations montre la difficulté qu'il y aurait à équilibrer un réacteur sur la base des seuls neutrons directs : sur la base de 40 000 générations par seconde, un (très faible) excès de réactivité de 0,01 % (soit 10 pcm) conduit au bout d'une seconde à un facteur d'augmentation de 1,000 140 000 = 55 si l'écart est positif, et de réduction de 0,999 940 000 = 0,018 si l'écart est négatif : on imagine difficilement dans ces conditions comment la réaction en chaîne peut être régulée.
Supercriticité prompte et retardée
La quasi-totalité des neutrons de fission (99,3 % pour l'uranium 235) sont émis instantanément (de l'ordre de 10−7 s). Pour une faible fraction des produits de fissions, il y a d'abord une désexcitation du noyau fils par radioactivité β, suivie de l'émission de neutrons dits « β-retardés » (ils sont émis avec la période de la désintégration β, de l'ordre de quelques secondes). Le schéma d'émission est le suivant[6] :
Les produits de fission qui émettent des neutrons retardés sont appelés « précurseurs ». Il s'agit par exemple de l'As-85, des Br-87, Br-88, Br-89 et Br-90, les Rb-93 et Rb-94, et les I-137 et I-138[7]. On a identifié plus de soixante précurseurs, dont les demi-vies s'étagent entre 0,12 s et 78 s. La loi de décroissance des neutrons retardés est donc théoriquement une somme d'autant d'exponentielles ; en pratique on obtient une très bonne approximation de cette loi par une somme de six exponentielles, ce qui revient à regrouper les précurseurs en six groupes de demi-vie homogène[6].
| Groupe | Précurseur typique | Énergie moyenne (MeV) | Demi-vie moyenne (s) | Fraction de neutrons émis (%) | ||||
|---|---|---|---|---|---|---|---|---|
| U-235 | Pu-239 | U-233 | U-235 | Pu-239 | U-233 | |||
| 1 | 87Br, 142Cs | 0,25 | 55,72 | 54,28 | 55,0 | 0,021 | 0,0072 | 0,0226 |
| 2 | 137I, 88Br | 0,56 | 22,72 | 23,04 | 20,57 | 0,140 | 0,0626 | 0,0786 |
| 3 | 138I, 89Br, (93 ; 94)Rb | 0,43 | 6,22 | 5,60 | 5,00 | 0,126 | 0,0444 | 0,0658 |
| 4 | 139I, (93 ; 94)Kr, 143Xe, (90 ; 92)Br | 0,62 | 2,3 | 2,13 | 2,13 | 0,252 | 0,0685 | 0,0730 |
| 5 | 140I, 145Cs | 0,42 | 0,61 | 0,618 | 0,615 | 0,074 | 0,018 | 0,0135 |
| 6 | (Br, Rb, As, etc) | - | 0,23 | 0,257 | 0,277 | 0,027 | 0,0093 | 0,0087 |
| Total | 0,64 | 0,21 | 0,26 | |||||
Les neutrons qui proviennent directement de la fission sont appelés des neutrons prompts, ceux qui proviennent de la radioactivité de la matière sont des neutrons retardés. La fraction de neutrons retardés dans le système est notée β, et sa valeur est typiquement inférieure à un pour cent du nombre total de neutrons dans une réaction en chaîne (0,7 % pour l'uranium). Elle décroît quand le numéro atomique du noyau qui fissionne croît.
C'est grâce à la présence de ces neutrons retardés qu'un réacteur nucléaire change de régime beaucoup plus lentement qu'il ne le ferait avec les neutrons prompts uniquement : sans ces neutrons retardés, les changements dans les taux de réaction des réacteurs seraient beaucoup trop rapides pour être contrôlés par des boucles de rétroactions techniques.
Il y a en fait deux types de situation supercritique : la supercriticité immédiate, et la supercriticité retardée.
- La zone de supercriticité comprise entre k = 1 et k = 1/(1-β) est dite de supercriticité retardée. C'est dans cette zone qu'opèrent tous les réacteurs nucléaires.
- De son côté, la zone où k > 1/(1-β) est dite de supercriticité prompte, c'est celle où opèrent les armes nucléaires.
Dans le jargon nucléaire, l'intervalle entre criticité et criticité prompte est appelé un « dollar ». C'est la valeur de la fraction de neutrons retardés, le β. L'écart de réactivité d'un réacteur par rapport à la criticité se mesure plus couramment en « cent », la centième partie du dollar. Si la proportion de neutrons retardés vaut β = 0,7 %, le dollar vaut 700 pcm et le cent vaut 7 pcm.
Remarque : Un réacteur à neutrons rapides ne fonctionne pas en « criticité prompte », mais bien au point critique comme tout réacteur : ces réacteurs sont stabilisés par les neutrons retardés, qui sont inhérents à toute réaction en chaîne. L'absence de modérateur (qui modifie le spectre de vitesse des neutrons après qu'ils sont produits) n'a pas d'incidence sur la présence de neutrons retardés (qui tirent leur nom du délai s'écoulant avant leur émission).
Différence entre criticité et criticité prompte
Un système est juste critique si chaque fission en engendre en moyenne exactement une autre. Dans ce cas, la réaction de fission est auto-entretenue.
Quand un atome d'uranium 235 subit une fission, il engendre typiquement deux ou trois neutrons (en moyenne 2,47). Dans ce cas, un système est critique si chaque neutron a une probabilité de 1/2,47 = 40,5 % de générer une autre fission (l'alternative étant de sortir du système, ou d'être absorbé par un atome sans provoquer de fission). On peut jouer sur cette probabilité en augmentant l'enrichissement isotopique de l'uranium (ce qui augmente le nombre d'atomes fissibles présents), ou en ralentissant les neutrons (en les laissant diffuser sur des atomes légers, appelés modérateurs), parce que l'atome U-235 capture plus facilement les neutrons lents (neutrons thermiques) que les neutrons rapides (la section efficace varie avec l'énergie des neutrons).
Dans un système sous-critique, chaque fission engendre en moyenne moins d'une nouvelle fission (k<1), et il faut des neutrons extérieurs à la chaîne pour entretenir la réaction. Si l'on injecte des neutrons dans un tel système, le nombre de neutrons découlant de cette injection décroît exponentiellement avec le temps. Si un tel système est soumis à un flux constant de neutrons, le flux induit est également constant, et la constante de proportionnalité est d'autant plus grande que k est proche de 1 : elle varie en 1/(1-k).
Dans un système juste critique, chaque fission en engendre une nouvelle : dans ce cas, si l'on injecte des neutrons, l'activité neutronique résultant de cette injection est constante au fil du temps. Si un tel système est soumis à un flux constant de neutrons, l'activité neutronique croît donc linéairement en fonction du temps.
Dans un système supercritique (k>1), le nombre de neutrons augmente exponentiellement en fonction du temps. Mais le comportement est très différent suivant que la criticité est atteinte uniquement avec les neutrons directs (supercriticité prompte), ou si elle n'est dépassée qu'avec les neutrons retardés (supercriticité retardée). Si le système n'est pas immédiatement supercritique, cette croissance reste relativement lente (typiquement, un doublement en quelques minutes). En revanche, si le système est dans la zone « supercritique prompte », l'augmentation du nombre de neutrons est extrêmement rapide, et conduit à une explosion si la situation est maintenue suffisamment longtemps par rapport à la durée de vie des neutrons directs — en l'occurrence, de l'ordre de quelques millionièmes de secondes, voire moins…
On peut considérer que dans un réacteur nucléaire à l'équilibre, les neutrons directs forment de leur côté un système sous-critique, soumis au flux (pratiquement statique à cette échelle de temps) des neutrons retardés. Le fonctionnement est équilibré lorsque la décroissance de la population des neutrons retardés est exactement compensée par les nouveaux noyaux excités produits par les fissions. Dans cette zone, en première approximation, l'activité neutronique croît donc linéairement en fonction du temps, ce qui permet un pilotage cybernétique de la réaction tant qu'elle ne s'écarte pas significativement de la situation juste critique.
Stabilité des réactions en chaîne
Généralités
Une réaction en chaîne a pour effet immédiat de produire de la chaleur, donc de faire varier la température du milieu critique. La réaction en chaîne peut se stabiliser sans réglage extérieur si le milieu est au départ proche de la criticité, et si la réactivité diminue quand la température augmente. Inversement, si un réacteur se trouve dans une configuration où la réactivité augmente avec la température, un écart de réactivité peut conduire à une situation explosive. Les réacteurs sont conçus pour fonctionner dans un régime stable, une instabilité ne pouvant résulter que d'un régime accidentel.
Combustible
Le premier effet pratiquement instantané d'une augmentation de température est l'effet Doppler sur les noyaux constitutifs du milieu, qui modifie la forme des résonances d'absorption neutroniques des matériaux présents. La résonance s'élargit et le pic s'abaisse à intégrale constante ; l'élargissement jouant bien davantage que l'abaissement des pics le résultat net est une augmentation des captures neutroniques par absorption résonnante[8].
Un second effet (plus macroscopique et moins important) est la dilatation thermique du combustible, qui va également dans le sens d'une stabilisation : la réactivité baisse quand la densité de matière fissile diminue.
Dans le cas d'un réacteur à eau pressurisée, l'ensemble des deux effets est exprimé par le coefficient de réactivité de température du combustible qui est voisin de - 2,5 pcm/°C.
En fonctionnement en puissance la température du combustible est plus élevée que celle du réfrigérant du cœur pour permettre la diffusion du flux de chaleur produite. L'effet en réactivité correspondant est appelé « intégrale de puissance », sa valeur dépend du dessin et de la nature du combustible utilisé. Un combustible métallique a ainsi une intégrale plus faible qu'un combustible oxyde.
Modérateur (réacteurs à neutrons thermiques ou lents)
Généralités
Un troisième effet est la dilatation thermique du modérateur qui, dans le cas des réacteurs à eau, est importante aux températures de fonctionnement, elle est nettement plus importante que celle du combustible ce qui fait diminuer le rapport de modération atomique (= nombre d'atomes d'hydrogène / nombre d'atomes fissiles) et diminuer la réactivité du réacteur (le keff) si le réseau est sous modéré. De même, en général, les fuites neutroniques augmentent quand la densité du modérateur diminue à cause de sa dilatation thermique ; l'effet réflecteur aux frontières du cœur est moins important.
Le coefficient de réactivité de température du modérateur peut valoir - 25 pcm/°C aux conditions de fonctionnement représentant sensiblement 10 °C de température du combustible.
Le réacteur à eau pressurisée ou bouillante est ainsi plus réactif aux températures ordinaires qu'aux conditions nominales, on appelle « reprise froid chaud » la valeur intégrale de l'écart de réactivité à puissance nulle entre les conditions ordinaires et les conditions de fonctionnement. Elle peut représenter jusqu'à 5000 pcm qui doivent être compensés par les moyens de contrôle tels que les barres ou la teneur en bore soluble.
On recense ci-après les différents effets jouant sur la valeur du coefficient de température du modérateur.
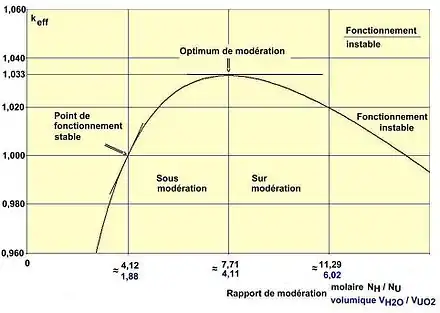
Optimum de modération
À la conception du cœur il est possible de choisir le rapport de modération c'est-à-dire le rapport entre la concentration volumique des atomes modérateurs et la concentration volumique des atomes fissiles. Par exemple de façon pratique dans le cas des réacteurs à eau pressurisée en faisant varier le pas régulier de disposition des crayons combustibles :
- si les crayons sont très rapprochés les uns des autres la quantité de modérateur offerte aux neutrons pour être ralentis est insuffisante et le rapport de multiplication en réseau infini k∞ diminue ;
- si les crayons sont très éloignés les uns des autres la probabilité qu'un neutron émis dans le combustible et thermalisé dans le modérateur rencontre un autre atome fissile diminue et le rapport de multiplication en réseau infini k∞ diminue ;
- entre les deux situations ci-dessus, il s'en trouve une ou le rapport : nombre d'atomes modérateurs / nombre d'atomes fissiles conduit au maximum de k∞ ; c'est l'optimum de modération
Dans le cas des réacteurs à eau pressurisée ou bouillante de façon à assurer la stabilité du réacteur on choisit un réseau sous modéré. De cette façon toute augmentation de température de l'eau ou a fortiori son ébullition se traduit par une diminution de k∞.
Température
La température du modérateur influe sur la valeur du coefficient de température pour la raison que la dilatabilité de l'eau augmente fortement avec la température aux conditions de fonctionnement. Ainsi la valeur absolue du coefficient de température diminue avec la température. Pour une valeur de l'ordre de - 25 pcm/°C aux conditions nominales (304,5 °C) (dilatabilité de l'eau = −2,21 kg/m3/K), on peut avoir à 100 °C - 8 pcm/°C (dilatabilité de l'eau = −0,70 kg/m3/K).
Pression
La pression du modérateur influe sur le coefficient de température du fait de la légère compressibilité du modérateur aux conditions de fonctionnement. L'eau étant réputée incompressible cet effet reste faible. Au voisinage des conditions de fonctionnement d'un REP, exprimé en pcm / bar, il est, en valeur absolue, 11 fois moins élevé que le coefficient de température modérateur en pcm / °C, soit donc environ 25/11 = 2,3 pcm/bar.
Usure du combustible
Au cours de l'usure du matériau fissile du cœur, le nombre d'atomes fissiles diminuant, le rapport de modération diminue et le coefficient de température modérateur augmente en valeur absolue.
Poison soluble
Les réacteurs électrogènes à eau pressurisée utilisent généralement l'acide borique dissous pour contrôler la réactivité à long terme dans le cours du fonctionnement[Note 1] ainsi que dans les cas incidentels ou accidentels. La concentration en acide borique d'un réacteur REP varie entre 0 et 2 000 ppm (partie par million). La valeur approximative de l'anti-réactivité d'un ppm (partie par million) de bore naturel dissous dans l'eau claire est voisine de 12 pcm et d'une dizaine autour de la teneur normale en fonctionnement[9]. À température ambiante l'eau est plus dense et la valeur du ppm de bore dissous est proche de 15 pcm/ppm. Pour s'affranchir de la limite de solubilité de l'acide borique on utilise également de l'acide borique enrichi en bore 10 (l'isotope le plus absorbeur de neutrons[10]).
L'utilisation d'acide borique dissous comme poison consommable peut conduire à un effet positif sur la réactivité (la dilatation de l'eau « fait sortir du cœur » une partie des atomes de bore). Si la teneur en bore est trop élevée au point de dépasser l'effet négatif apporté par la dilatation du modérateur un effet positif peut être constaté : c'est ce qui limite la teneur en bore dans le circuit primaire des réacteurs à eau pressurisée électrogènes.
Poisons consommables solide
L'effet des poisons consommables solides dépend du mode choisi pour leur implantation et des caractéristiques de la capture résonnante qu'elle peut présenter.
Effet de vide
Une augmentation de température peut conduire le fluide caloporteur à ébullition locale. Le plus souvent, le vide relatif créé par l'ébullition a un effet négatif (donc stabilisant) sur la réactivité, et le système se stabilise alors au point d'ébullition. Cependant ce n'est pas le cas dans toutes les configurations ; ce coefficient de vide peut conduire certains types de réacteurs à l'instabilité dans certaines conditions atypiques (ce qui s'est passé lors de la catastrophe de Tchernobyl).
En cas de fuite du modérateur (sous forte pression et en température dans le cas des réacteurs à eau pressurisée) une ébullition importante et rapide est créée à court terme dans le cœur (l'eau est remplacée par de la vapeur), il est donc indispensable que l'« effet de vide » soit négatif.
Passage en réactivité prompte

Si l'excès de réactivité a été très important, au point d'atteindre une réactivité prompte, la vaporisation partielle du cœur porté soudainement à haute température créé une surpression brutale et une onde de choc qui entraîne sa dislocation : le cœur explose. L'énergie libérée par de telles explosions dépend en partie de la résistance du cœur à la dislocation, qui le maintient plus longtemps dans un état critique, et surtout de la vitesse à laquelle la réactivité a augmenté : c'est pour cette raison que les commandes d'un réacteur sont conçues pour ne pas permettre à la réactivité d'augmenter plus rapidement qu'une valeur limite fixée par la sécurité. Dans le cas d'un réacteur nucléaire, cette explosion risque de provoquer la rupture de la cuve du réacteur et de l'enceinte de confinement, qui doivent donc être dimensionnés pour résister à ces accidents extrêmes[11].
En situation accidentelle, la vitesse de variation de la réactivité ne peut pas atteindre celle visée dans une arme nucléaire : un système qui devient accidentellement critique reste en pratique proche de la criticité jusqu'à ce que l'énergie accumulée soit suffisante pour le rendre à nouveau sous-critique. En tout état de cause, l'énergie qui permet de provoquer in fine la dispersion (ou la dislocation) de la masse critique est de l'ordre de grandeur des énergies disponibles dans un explosif chimique, très largement inférieure à celle libérée par une explosion nucléaire proprement dite. C'est le mécanisme décrit par le premier Mémorandum de Frisch et Peierls, qui concluait à l'impossibilité d'obtenir une explosion nucléaire à partir d'uranium non enrichi :
- When the temperature reaches several thousand degrees the container of the bomb will break and within 10−4 sec the uranium would have expanded sufficiently to let the neutrons escape and so to stop the reaction. The energy liberated would, therefore, be only a few times the energy required to break the container, i.e. of the same order of magnitude as with ordinary high explosives. (Quand la température atteindra plusieurs milliers de degrés, l'enveloppe de la bombe se désagrégera, et en 10−4 secondes l'uranium sera suffisamment dispersé pour que les neutrons s'échappent et arrêtent la réaction. L'énergie libérée serait, par conséquent, guère plus forte que celle nécessaire pour désagréger l'enveloppe, c'est-à-dire du même ordre de grandeur que celle dégagée par des explosifs performants)[12].
C'est à la suite de cette première conclusion que les conditions nécessaires pour une explosion nucléaire ont été formalisées : l'assemblage d'une masse critique suffisante pour atteindre une prompt-criticité, sans passer par un modérateur donc avec des neutrons rapides, et une vitesse de passage à la criticité la plus élevée possible :
- It is important that the assembling of the parts should be done as rapidly as possible, in order to minimize the chance of a reaction getting started at a moment when the critical conditions have only just been reached. If this happened, the reaction rate would be much slower and the energy liberation would be considerably reduced; it would, however, always be sufficient to destroy the bomb. (Il est fondamental que l'assemblage critique se fasse aussi rapidement que possible, de manière à éviter que la réaction ne démarre alors que la criticité vient à peine d'être atteinte. Dans ce cas, le taux de réaction serait bien moindre, et l'énergie libérée serait considérablement réduite ; elle serait néanmoins toujours suffisante pour détruire la bombe)[12].
Explosion atomique
Pour réaliser une explosion atomique, il faut faire passer très rapidement une masse de matière fissile dans un état prompt critique.
- Pour une masse donnée de matière fissile, la valeur de la réactivité k peut être augmentée en augmentant la densité : la probabilité qu'un neutron rencontre un noyau sur une distance donnée étant proportionnelle à la densité de matière, quand on augmente la densité de matière fissile on augmente d'autant la réactivité. C'est cette méthode qui est utilisée dans la méthode par implosion. Dans ces engins, la réaction en chaîne démarre après que la densité de matière a été augmentée par le choc engendré par un explosif conventionnel.
- Dans la méthode par rapprochement, deux blocs sous-critiques sont mis en contact rapidement. La valeur de la réactivité d'un ensemble est toujours supérieure à celle de chacune de ses parties, d'une manière qui dépend de la distance entre les blocs et de leur orientation. L'assemblage des deux blocs peut être suffisant pour faire passer l'ensemble dans un état critique.
- En théorie, la valeur de la criticité peut également être augmentée en insérant un réflecteur à neutrons.
Pendant que le système évolue vers l'état visé, il est d'abord sous-critique, puis passe par un état juste critique, et il faut que sa criticité continue à augmenter jusqu'à devenir nettement sur-critique, des neutrons étant injectés pour déclencher la réaction en chaîne au moment optimal.
Une fois que la masse de matière nucléaire est dans un état prompt supercritique et que la réaction en chaîne a été déclenchée, la puissance massique dégagée augmente exponentiellement. Si les neutrons, n'étant pas modérés, ont une durée de vie de l'ordre de 10−7 seconde ; et si l'excès de réactivité atteint avant que la réaction en chaîne ne démarre est par exemple de sept pour cent, la puissance augmente en 1,07 (t/10−7) : elle double chaque millionième de seconde. Cette augmentation brusque de puissance transforme instantanément la matière nucléaire en plasma de très haute pression, créant une onde de choc. À ce point, si le taux de combustion de l'explosion a été significatif, la consommation de matière fissile fait diminuer sa densité, mais de toute manière l'onde de choc disperse le dispositif. Avec la chute de densité la réactivité redevient négative et la réaction s'arrête.
Pour réaliser une arme nucléaire, il faut amener la matière fissile dans son état supercritique optimal très rapidement. En effet, la fission spontanée provoque des émissions de neutrons dans la matière fissile. Dès que le système a franchi l'état critique, ces neutrons peuvent à tout moment déclencher une réaction en chaîne, et faire exploser l'assemblage avant qu'il n'ait atteint son état optimal. C'est ce que l'on appelle une « pré-détonation ». Pour que la probabilité d'une telle pré-détonation reste faible, la probabilité qu'un seul neutron puisse être émis entre le passage à l'état critique et l'état optimal doit être négligeable. Pour cela, la conception de l'engin doit être telle que le temps de passage à l'état de réactivité maximal est le plus court possible, et l'on utilise des matières fissiles qui n'ont qu'un faible taux d'émissions spontanées de neutrons.
Par kilogramme de matière fissile, l'uranium 235 produit 0,3 neutron par seconde, le plutonium 239 en produit 22, pratiquement cent fois plus ; mais surtout le Pu-239 contient toujours une fraction de Pu-240 qui produit 920 neutrons par gramme. C'est à cause du Pu-240 qu'il n'est pas possible de réaliser une arme par rapprochement en utilisant du plutonium comme matière fissile : le temps nécessaire au rapprochement est trop long pour que l'arme soit fiable. C'est également pour cette raison que le taux de plutonium 240 doit être le plus faible possible pour un plutonium dit « de qualité militaire ».
Notes et références
Notes
- L'utilisation du bore dissous dans le cas des réacteurs bouillants se limite aux cas incidentels sérieux ou accidentels du fait du risque de clarification de l'eau contenue dans la cuve par le débit alimentaire exempt de bore en exploitation normale
- Calculée à l'article Flux neutronique
- Calculée à l'article Flux neutronique
Références
- (en) Improvements in or relating to the transmutation of chemical elements, (lire en ligne)
- Francis Perrin, « Calcul relatif aux conditions éventuelles de transmutation en chaîne de l’uranium », Académie des sciences, (CRAS 208-1394 & 1573.
- Noyaux et particules - Joliot: réaction en chaîne (Alain Bouquet, directeur de recherche au CNRS), cosmologie.wordpress.com, blog d'Alain Bouquet (consulté le 16 avril 2022).
- « Google Patents », sur patents.google.com (consulté le ).
- Sigvard Eklung, Oklo - Un réacteur nucléaire qui a fonctionné il y a 1800 millions d'années, , 4 p. (Oklo - Un réacteur nucléaire qui a fonctionné il y a 1 800 millions d'années)
- D'après Determination of delayed neutron parameters and of uranium content of a sample, Dr. Csaba Sükösd, Budapest University of Technology and Economics
- D'après Radioprotection et ingénierie nucléaire de Henri Métivier, Inc NetLibrary, Institut national des sciences et techniques nucléaires, p. 214.
- Paul Reuss, Précis de neutronique, INSTN, 2003.
- Physique des Réacteurs Nucléaires Peter Baeten, SCK-CEN, Centre d'Etudes de l'Energie Nucléaire, consulté le 08 mai 2020
- Absorbeurs de neutrons Cadmium et bore : deux efficaces absorbeurs de neutrons laradioactivite.com, consulté le 08 mai 2020
- Thermohydraulique des réacteurs, Jean-Marc Delhaye, INSTN
- Frisch-Peierls Memorandum, "On the Construction of a "Super-bomb" based on a Nuclear Chain Reaction in Uranium" mars 1940
Voir aussi
Liens internes
- Accident de criticité
- Bombe nucléaire
- Centrale nucléaire
- Combustible nucléaire
- Énergie de liaison atomique
- Énergie nucléaire
- Fission nucléaire
- Fission spontanée
- Flux neutronique
- Formule des quatre facteurs
- Fraction de neutrons retardés
- Long feu
- Masse critique (réaction nucléaire)
- Physique nucléaire
- Produit de fission
- Réacteur nucléaire
- Réaction nucléaire
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :
- (en) Animation de réaction en chaîne
- (en) Lettre d'Einstein's au Président Roosevelt - 1939
- Portail de la physique
- Portail du nucléaire
