Racine carrée de trois
La racine carrée de trois, notée √3 ou 31/2, est en mathématiques le nombre réel positif dont le carré est 3 exactement. Il vaut approximativement 1,732[1]. On l’appelle parfois constante de Théodore[2] parce que Théodore de Cyrène a démontré son irrationnalité.

En histoire des sciences ou en pédagogie, commence à exister dans des
considérations d’aires. À gauche d’une similitude qui multiplie
les aires par 3. À droite une relation de Pythagore est prouvée en décomposant
de plusieurs façons un motif répétitif d’un pavage de Pythagore.
considérations d’aires. À gauche d’une similitude qui multiplie
les aires par 3. À droite une relation de Pythagore est prouvée en décomposant
de plusieurs façons un motif répétitif d’un pavage de Pythagore.
| Liste des nombres - Nombres irrationnels √2 - φ - √3 - √5 - e - π | |
| Binaire | 1.1011101101100111101... |
| Décimal | 1.7320508075688772935... |
| Hexadécimal | 1.BB67AE8584CAA73B... |
| Fraction continue | |
Éléments introductifs
- √3 se prononce racine carrée de 3 ; se prononçait aussi « radical de trois ».
- √3 se note également 31/2 : Trois puissance un demi (notation Unicode : 3½).
Algèbre
- De même que √2, √3 est un irrationnel quadratique.
- Les racines cubiques de l'unité sont
Analyse
√3 est égal au radical imbriqué .
Géométrie
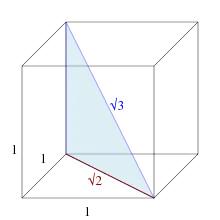
Diagonale d'un cube unité.
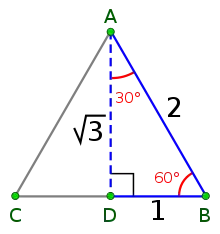
Proportions entre le côté d'un triangle équilatéral et sa hauteur.
La diagonale d'un cube de côté 1 mesure √3.
La hauteur d'un triangle équilatéral de côté 1 est égale à √3/2. Cette propriété entraîne les suivantes :
- la distance entre deux côtés opposés d'un hexagone régulier de côté 1 est égale à √3 ;
- √3 est le rapport entre la largeur (distance entre les extrémités du poisson sans la queue) et la hauteur de la figure Vesica piscis. On peut le montrer en construisant deux triangles équilatéraux à l'intérieur de la figure.
Notes et références
- Pour dix millions de décimales, voir la suite A002194 de l'OEIS.
- (en) Eric W. Weisstein, « Theodorus' Constant », sur MathWorld avec bibliographie et liens vers l'OEIS pour son développement en système décimal, en système binaire, et en fraction continue.
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.