Singularité de Schwarzschild

En utilisant la coordonnée radiale “isotrope” ${\displaystyle {\underline {r}}}$ la métrique précédente peut s'écrire sous la forme[1]^,[2]^,[3] :

${\displaystyle ds^{2}=A({\underline {r}})~c^{2}dt^{2}-{\underline {B}}({\underline {r}})~(d{\underline {r}}^{2}+{\underline {r}}^{2}d\theta ^{2}+{\underline {r}}^{2}sin^{2}(\theta )~d\phi ^{2})}$

avec : ${\displaystyle ~A({\underline {r}})={\Big (}{\frac {{\underline {r}}-{\underline {R}}_{s}}{{\underline {r}}+{\underline {R}}_{s}}}{\Big )}^{2}}$ ; ${\displaystyle ~{\underline {B}}({\underline {r}})={\Big (}1+{\frac {{\underline {R}}_{s}}{\underline {r}}}{\Big )}^{4}~}$ ; ${\displaystyle ~{\underline {R}}_{s}={\frac {GM}{2c^{2}}}={\frac {R_{s}}{4}}}$.

Cette formulation de la métrique est dite “isotrope” car la partie spatiale est proportionnelle à ${\displaystyle ~(d{\underline {r}}^{2}+{\underline {r}}^{2}d\theta ^{2}+{\underline {r}}^{2}sin^{2}(\theta )~d\phi ^{2})~}$ qui correspondrait à un espace plat (donc isotrope).

Le changement de variable correspond à :

${\displaystyle r={\underline {r}}~.{\Big (}1+{\frac {{\underline {R}}_{s}}{\underline {r}}}{\Big )}^{2}~}$ ; ${\displaystyle ~~{\underline {r}}={\frac {r}{2}}~.\left({\Big (}1-{\frac {R_{s}}{2r}}{\Big )}\pm {\sqrt {1-{\frac {R_{s}}{r}}}}~\right).}$

Ces relations permettent de vérifier la correspondance : ${\displaystyle ~{\underline {r}}={\underline {R}}_{s}~\Leftrightarrow ~r=R_{s}.}$

Or, on constate que la forme isotrope de la métrique ne présente clairement pas de singularité spatiale pour ${\displaystyle ~{\underline {r}}={\underline {R}}_{s}~~;~}$ il semble donc que cette singularité apparente est essentiellement due à l'utilisation de la variable ${\displaystyle ~r}$.

Démonstration

On peut calculer ${\displaystyle ~A({\underline {r}})~}$ et ${\displaystyle ~{\underline {B}}({\underline {r}})~}$ en résolvant les équations d'Einstein pour le champ de gravitation dans le vide, mais en comparant les deux formes précédentes de la métrique, la correspondance impose :

${\displaystyle {\underline {B}}({\underline {r}})~d{\underline {r}}^{2}=B(r)~dr^{2}~~}$ et ${\displaystyle ~~{\underline {B}}({\underline {r}})~{\underline {r}}^{2}=r^{2}.}$

La comparaison permet d'écrire : ${\displaystyle ~{\frac {d{\underline {r}}}{\underline {r}}}=\pm ~{\sqrt {B(r)}}~~{\frac {dr}{r}}=\pm ~{\frac {dr}{\sqrt {r~.(r-R_{s})}}}.}$

L'intégration peut être simplifiée en remarquant que : ${\displaystyle ~r~.(r-R_{s})={\Big (}r-{\frac {R_{s}}{2}}{\Big )}^{2}-{\Big (}{\frac {R_{s}}{2}}{\Big )}^{2}.}$

La constante peut être encore simplifiée en choisissant la variable : ${\displaystyle ~u={\frac {2}{R_{s}}}~{\Big (}r-{\frac {R_{s}}{2}}{\Big )}={\frac {2r}{R_{s}}}-1~~;~}$ ainsi : ${\displaystyle ~{\frac {d{\underline {r}}}{\underline {r}}}=\pm ~{\frac {du}{\sqrt {u^{2}-1}}}.}$

L'intégration donne ensuite : ${\displaystyle ~ln({\underline {r}})=\pm ~arcosh(u)+Cste,~}$ mais il semble plus pratique d'utiliser l'expression logarithmique de arcosh :

${\displaystyle ~ln({\underline {r}})=\pm ~ln{\Big (}u+{\sqrt {u^{2}-1}}{\Big )}+Cste.}$

La constante peut être déterminée en considérant que l'espace est asymptotiquement plat à l'infini :

${\displaystyle ~B\rightarrow 1~}$ ; ${\displaystyle ~{\underline {B}}\rightarrow 1~}$ ; ${\displaystyle ~r\rightarrow \infty ~}$ ; ${\displaystyle ~u\rightarrow \infty ~}$ ; ${\displaystyle ~{\underline {r}}\rightarrow \infty ~}$ ;

${\displaystyle ~{\underline {r}}\approx r~}$ ; ${\displaystyle ~u\approx {\frac {2r}{R_{s}}}~}$ ; ${\displaystyle ~ln{\Big (}u+{\sqrt {u^{2}-1}}{\Big )}\approx ln(2u)\approx ln(r)-ln({\underline {R}}_{s}).}$

Ainsi dans cette limite le signe ${\displaystyle \pm }$ correspond forcément au signe ${\displaystyle +}$ et la constante d'intégration est ${\displaystyle ~ln({\underline {R}}_{s})}$ :

${\displaystyle ~{\underline {r}}={\underline {R}}_{s}~.{\Big (}u+{\sqrt {u^{2}-1}}{\Big )}={\frac {r}{2}}~.\left({\Big (}1-{\frac {R_{s}}{2r}}{\Big )}+{\sqrt {1-{\frac {R_{s}}{r}}}}\right)~;}$

(à ce niveau, il faut encore chercher à quoi correspond l'autre possibilité pour le signe ${\displaystyle \pm }$).

On peut alors inverser la relation (en isolant le radical, en élevant au carré et en simplifiant) : ${\displaystyle ~r={\underline {r}}~.{\Big (}1+{\frac {{\underline {R}}_{s}}{\underline {r}}}{\Big )}^{2}.}$

Ce changement de variable vérifie la correspondance : ${\displaystyle ~{\underline {r}}={\underline {R}}_{s}~\Leftrightarrow ~r=R_{s},~}$ mais si on inverse à nouveau cette relation, on obtient ici encore un signe ${\displaystyle \pm }$ :

${\displaystyle ~{\underline {r}}={\frac {r}{2}}~.\left({\Big (}1-{\frac {R_{s}}{2r}}{\Big )}\pm {\sqrt {1-{\frac {R_{s}}{r}}}}\right).}$

On constate alors que l'option avec le signe ${\displaystyle -}$ correspond à la limite :

${\displaystyle ~r\rightarrow \infty ~}$ ; ${\displaystyle ~u\rightarrow \infty ~}$ ; ${\displaystyle ~{\underline {r}}\rightarrow 0~}$ ;

${\displaystyle ~r\approx {\frac {{{\underline {R}}_{s}}^{2}}{\underline {r}}}~}$ ; ${\displaystyle ~u\approx {\frac {2r}{R_{s}}}~}$ ; ${\displaystyle ~ln{\Big (}u+{\sqrt {u^{2}-1}}{\Big )}\approx ln(r)-ln({\underline {R}}_{s})~~;}$

${\displaystyle ln({\underline {r}})\approx -~ln(r)+ln({\underline {R}}_{s})+Cste~}$ où la constante d'intégration est ici encore ${\displaystyle ~ln({\underline {R}}_{s})~}$ par comparaison.

On a donc effectivement trouvé ainsi la solution complète de l'équation différentielle.

On retrouve enfin en reportant simplement : ${\displaystyle ~{\underline {B}}({\underline {r}})={\frac {r^{2}}{{\underline {r}}^{2}}}={\Big (}1+{\frac {{\underline {R}}_{s}}{r}}{\Big )}^{4}~;~}$ puis en reportant de même et en simplifiant : ${\displaystyle ~A({\underline {r}})=A(r({\underline {r}}))={\Big (}{\frac {{\underline {r}}-{\underline {R}}_{s}}{{\underline {r}}+{\underline {R}}_{s}}}{\Big )}^{2}.}$

 

♦ remarque : la comparaison avec le repérage de Lemaître semble par contre indiquer que c'est le dépassement de la vitesse ${\displaystyle c}$ (par rapport au repérage statique) qui est à l'origine de la singularité : Lemaître considère un repérage co-mobile avec une particule en chute libre, dont la vitesse atteint (puis dépasse formellement) ${\displaystyle c}$ au niveau de la singularité ; ce repérage évite la singularité spatiale liée à la divergence de ${\displaystyle B~}$, mais d'ailleurs aussi l'effet temporel lié à l'annulation de ${\displaystyle A~}$, justifiant l'origine du problème dans le fait que le repérage statique serait pour cela inadapté (impossibilité d'un référentiel statique pour ${\displaystyle ~r<R_{s}~}$ car aucun corps de référence ne peut y rester immobile).

On constate en outre qu'au passage de la pseudo-singularité ${\displaystyle ~A({\underline {r}})~}$ s'annule sans devenir négatif : la coordonnée ${\displaystyle ~t~}$ reste une variable temporelle.

Cette différence de comportement entre ${\displaystyle ~A({\underline {r}})~}$ isotrope et ${\displaystyle ~A(r)~}$ classique est physiquement incompatible pour une métrique statique.

La quantité ${\displaystyle A}$ est une propriété associée au point ${\displaystyle P}$ de l'espace (fixe) où elle est calculée : en un point fixe la grandeur ${\displaystyle ~A={\frac {d\tau ^{2}}{dt^{2}}}~}$ est invariante dans ce changement de coordonnée radiale. Les expressions ${\displaystyle A(r)}$ et ${\displaystyle A({\underline {r}})}$ diffèrent car le repérage de ${\displaystyle P}$ utilise une variable différente, mais le résultat ${\displaystyle ~A={\Big (}1-{\frac {R_{s}}{r}}{\Big )}={\Big (}{\frac {{\underline {r}}-{\underline {R}}_{s}}{{\underline {r}}+{\underline {R}}_{s}}}{\Big )}^{2}~}$ est le même (c'est pour cela qu'on ne note pas ${\displaystyle ~{\underline {A}}}$). Non ambigu pour une métrique statique, le temps durée au point ${\displaystyle P}$ est indépendant de la façon dont on repère la position de ce point.

Variations (en notations réduites) de la variable radiale classique en fonction de la variable radiale isotrope.

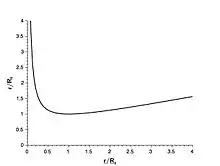
La raison de cette différence, qui n'est qu'apparente, vient du caractère non bijectif de la relation entre ${\displaystyle ~r~}$ et ${\displaystyle ~{\underline {r}}~.~}$ Si on se base sur les coordonnées isotropes, alors pour ${\displaystyle ~{\underline {r}}<{\underline {R}}_{s}~}$ (à l'intérieur de la zone singulière) on obtient ${\displaystyle ~r>R_{s}~}$ (cf. figure 1) ; ceci conserve ${\displaystyle ~A(r)>0~}$ et ${\displaystyle ~B(r)>0,~}$ ainsi la coordonnée ${\displaystyle ~t~}$ reste du genre temps et la coordonnée ${\displaystyle ~r~}$ reste du genre espace, de même qu'avec les coordonnées isotropes.

En pratique, la variable ${\displaystyle ~r~}$ est déterminée d'après le périmètre : ${\displaystyle ~r={\frac {1}{2\pi }}\int _{0}^{2\pi }r~d\theta ={\frac {1}{2\pi }}\int _{0}^{2\pi }{\sqrt {{\underline {B}}({\underline {r}})}}~{\underline {r}}~d\theta ~}$ ; il s'agit d'un rayon périphérique. Or l'espace issu des équations d'Einstein dans le vide n'étant pas plat, rien ne dit a priori que cette variable ${\displaystyle ~r~}$ est bien appropriée pour décrire l'éloignement du centre. Il peut être préférable d'utiliser un rayon intérieur ${\displaystyle ~r_{int}~}$ : distance au centre, déterminée d'après ${\displaystyle ~\int {\sqrt {{\underline {B}}({\underline {r}})}}~~d{\underline {r}}=\int \pm ~{\sqrt {B(r)}}~~dr~.~}$

Or la variable ${\displaystyle ~{\underline {r}}~}$ est partout croissante en fonction de ${\displaystyle ~r_{int},~}$ mais en comparant aux coordonnées isotropes, la variable ${\displaystyle ~r~}$ passe par un minimum ${\displaystyle ~R_{s}~}$ au niveau de ${\displaystyle ~{\underline {r}}={\underline {R}}_{s}~:}$ à cause de la forte courbure de l'espace, des sphères ayant un rayon intérieur plus petit, peuvent pourtant avoir un rayon périphérique plus grand.

Remarque : cette caractéristique inusuelle fait que les coordonnées isotropes, pourtant parfaitement solution des équations d'Einstein dans le vide, sont le plus souvent évitées lors de l'étude de l'horizon de Schwarzschild ; il est alors considéré que la partie extérieure est valide, mais que le prolongement intérieur n'est solution que par un artifice mathématique fortuit.

Rien n'interdit alors d'utiliser des coordonnées comme celles de Kruskal-Szekeres, mais pour obtenir une description équivalente à celle des coordonnées isotropes, il faut en exclure les valeurs correspondant à ${\displaystyle ~r<R_{s}~~}$ (on peut obtenir des valeurs ${\displaystyle ~r<R_{s}~}$ dans le prolongement de la métrique de Schwarzschild à l'intérieur d'un astre, mais c'est impossible dans le vide).

Remarque : cela s'obtient en découpant les zones (II) et (IV) décrivant ${\displaystyle ~r<R_{s}~}$ dans le diagramme de Kruskal, puis en raccordant de part et d'autre les zones (I) et (III) décrivant ${\displaystyle ~r>R_{s}~}$ (la zone (III) considérée par Kruskal comme extérieur 2 est considérée comme intérieur en coordonnées isotropes) ; de ce point de vue, la métrique isotrope peut être considérée comme incomplète.

Pour aider la compréhension des caractéristiques de cette métrique, il peut être intéressant d'en proposer une (des) représentation(s) graphique(s).

Il n'est pas possible de représenter l'espace-temps dans ${\displaystyle \mathbb {R} ^{3}}$, mais on peut représenter un “plan” de l'espace dans ${\displaystyle \mathbb {R} ^{3}}$.

En outre, une représentation de l'espace peut aussi aider à comprendre le comportement temporel puisque dans le vide ${\displaystyle ~B(r)={\frac {1}{A(r)}}.}$

On commence par simplifier la partie angulaire en imposant ${\displaystyle ~\theta ={\frac {\pi }{2}}~}$ et en considérant la métrique du plan :

${\displaystyle ds^{2}=A(r)~c^{2}dt^{2}-dl^{2}~~}$ avec ${\displaystyle ~~dl^{2}=B(r)~dr^{2}+r^{2}d\phi ^{2}.}$

On cherche ensuite, en coordonnées cylindriques ${\displaystyle ~(r,\phi ,z)~}$ dans ${\displaystyle \mathbb {R} ^{3},~}$ une équation de surface reliant ${\displaystyle ~r~}$ et ${\displaystyle ~z~}$ (indépendante de ${\displaystyle \phi }$ par symétrie), telle que sa métrique spatiale soit la même que celle de Schwarzschild.

Cela impose : ${\displaystyle ~dl^{2}=dr^{2}+r^{2}d\phi ^{2}+dz^{2}~~}$ ; ${\displaystyle ~~{\frac {r}{r-R_{s}}}dr^{2}=dr^{2}+dz^{2}.}$

L'intégration donne : ${\displaystyle ~{\frac {r}{R_{s}}}=1+{\Big (}{\frac {z}{2R_{s}}}{\Big )}^{2}~~;~~}$ il s'agit d'un paraboloïde de révolution.

Pour le cas d'un astre stable, on peut montrer que la représentation graphique équivalente à l'intérieur ressemble à une portion de sphère (exactement pour une masse volumique uniforme et très supérieure à la pression, ce qui est souvent une bonne approximation pour les petits astres, mais aussi pour de grandes structures à l'échelle cosmique). Le raccordement à la surface de l'astre se fait sans laisser apparaître la singularité[2]^,[4].

Schématisation graphique de la géométrie spatiale au voisinage d'un astre.

Pour un hypothétique trou noir considéré comme solution des équations dans le vide, non causé par un astre, la représentation graphique au delà de l'horizon n'a pas de signification en coordonnées classiques, dans la mesure où l'espace ne peut pas y être statique (la variable ${\displaystyle ~r~}$ cesse d'être de type espace).

Avec les coordonnées isotropes, la partie au delà de l'horizon est symétrique et on obtient une allure analogue à celle d'un “trou de ver” (qui est un objet différent[3]^,[5]).

Schématisation graphique de la géométrie spatiale au voisinage d'une singularité de Schwarzschild.

Pour un hypothétique astre (instable) dont la singularité serait extérieure, la situation serait intermédiaire, avec un raccordement dans la partie inversée (impossible en coordonnées classiques).

Citées, de façon anecdotique, dans la plupart des ouvrages de référence, les coordonnées isotropes ne sont généralement pas décrites plus en détail. Cela en partie parce qu'elles sont d'usage un peu moins pratique que les coordonnées classiques, mais aussi à cause des propriétés étranges qu'elles décrivent au delà de l'horizon des événements ; en particulier un aspect de gravitation répulsive. Seuls quelques auteurs écrivent de temps à autres des articles de vulgarisation (pour initiés), afin d'en entretenir la connaissance (utile pour montrer que l'interprétation physique des solutions mathématiques n'est pas forcément évidente)[6].

On peut résoudre les équations du mouvement [6] mais il suffit de raisonner par symétrie : si, au delà de l'horizon, l'utilisation de ${\displaystyle ~{\underline {r}}~}$ revient à augmenter à nouveau ${\displaystyle ~r~}$ depuis ${\displaystyle ~R_{s}~}$ jusqu'à l'infini, alors la métrique isotrope y décrit les mêmes phénomènes que la métrique classique avec ces valeurs de ${\displaystyle ~r~}$ : un effet gravitationnel symétrique par rapport à l'horizon.

Ainsi la gravitation serait répulsive de l'autre côté de la singularité, ou bien dit autrement : l'attraction y serait dans l'autre sens, toujours vers la singularité (c'est-à-dire orientée dans le sens où les lignes de champ se resserrent).

Précisions

Cette section ne cite pas suffisamment ses sources (juillet 2022). 

Pour l'améliorer, ajoutez des références de qualité et vérifiables (comment faire ?) ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Il ne s'agit pas au sens strict de gravitation répulsive, ce qui correspondrait à une équation d'Einstein d'une forme telle que l'énergie-impulsion provoquerait une courbure spatio-temporelle de signe contraire : ${\displaystyle \ \ R_{\mu \nu }-{\frac {1}{2}}\,g_{\mu \nu }\,R\ =-\kappa T_{\mu \nu }\ \ }$ (ici hors de propos).

Ici, il faut au contraire se rappeler que la théorie gravitationnelle d'Einstein est de type géométrique : l'énergie-impulsion courbe l'espace-temps, la gravitation y intervient alors comme une force d'inertie (au sens figuré).

On peut alors partir de l'exemple de la force centrifuge dans un espace plat (en mécanique newtonienne) : l'effet décrit par la force centrifuge découle de l'écart du mouvement par rapport aux géodésiques d'espace.

Dans un plan, l'écart d'un mouvement circulaire par rapport à la tangente (géodésique rectiligne) est décrit par une force centrifuge (qui tend à éloigner la particule du cercle).

la force centrifuge décrit l'éloignement du géodésique (rectiligne)

L'effet est a priori tout à fait semblable dans un espace courbe, par exemple sur la surface d'une sphère (dont les géodésiques sont des grands cercles), pour un mouvement circulaire de rayon modéré (ici encore selon les principes de la mécanique newtonienne).

la force centrifuge décrit l'éloignement du géodésique (grand cercle de la sphère)

Par contre il est inversé si le rayon du cercle (distance au centre) est assez grand pour que son périmètre redevienne plus petit que celui de la sphère : la force nommée centrifuge devient centripète.

la force centrifuge décrit l'éloignement du géodésique (grand cercle de la sphère)

◇ remarque : prétendre raisonner en mécanique newtonienne dans un espace courbe (surface d'une sphère) ne consiste pas à utiliser plus ou moins la relativité générale ; d'une part cette dernière raisonne dans l'espace-temps ; d'autre part on peut modéliser le mouvement sur une sphère avec un point matériel lié, par une tige rigide de masse négligeable, à une rotule idéale située en un point fixe.

La gravitation répulsive décrite par les coordonnées isotropes est un effet de ce type (en relativité générale).

 

Ceci rendrait impossible la formation d'un trou-noir stellaire statique (astre dont la singularité serait extérieure) : par continuité, la matière en surface subirait un champ répulsif, puisque voisin de celui dans le vide juste au dessus, donc elle serait éjectée (et cela jusqu'à ce que cessent les conditions donnant lieu à l'effondrement, ou que toute la matière de l'astre ait été éjectée en supernova).

Cela est sans rapport avec les autres raisons pouvant faire douter de l'existence des trous noirs ; en particulier l'équilibre thermodynamique d'une étoile semble imposer une limitation de la singularité à un maximum d'environ 50 % à 70 % (selon les modèles) de la taille de l'étoile, donc toujours à l'intérieur[2].

La métrique de Schwarzschild ne présente pas de singularité spatio-temporelle pour ${\displaystyle ~r=R_{s}~}$ du fait que le déterminant ${\displaystyle -r^{4}sin^{2}(\theta )~}$ de sa matrice est non nul pour cette valeur. Cette singularité est donc due simplement aux coordonnées choisies, et un référentiel mieux adapté peut éviter ce problème purement mathématique[7].

L'annulation du coefficient de ${\displaystyle ~dt^{2}~}$ au niveau du rayon de Schwarzschild a par contre des propriétés singulières. En particulier le temps ne s'y écoule pas aux yeux d'un observateur lointain. Aux yeux de ce même observateur, les corps en chute vers le rayon de Schwarzschild s'en approchent de manière asymptotique (suivant une loi exponentielle du temps) sans jamais l'atteindre, et la durée de la chute est alors infinie[7].

Les quelques exemples qui précèdent indiquent que la représentation isotrope correspond à un espace physique différent de celui décrit par les coordonnées classiques. Dans la mesure où l'application de la méthode de Lemaître conduit à conclure à un effondrement, contrairement à ce que prévoit le repérage isotrope (avec une gravitation répulsive de l'autre côté, il prévoit des oscillations de part et d'autre le l'horizon, de période paraissant infinie pour les observateurs éloignés[6]), on en déduit généralement qu'il s'agit d'un artifice mathématique et que les coordonnées isotropes sont inadaptées.

Il est toutefois possible d'appliquer aux coordonnées isotropes une transformation “de type Lemaître" modifiée pour être compatible avec ces coordonnées (la vitesse d'effondrement atteignant c au niveau de l'horizon, puis diminuant symétriquement) ; il s'agit donc bien d'une description mathématique cohérente d'un autre espace physique. Il est difficile d'imaginer des tests expérimentaux permettant de les discriminer.