Projection cartographique
La projection cartographique est un ensemble de techniques géodésiques permettant de représenter une surface non plane (surface de la Terre, d'un autre corps céleste, du ciel, ...) dans son ensemble ou en partie sur la surface plane d'une carte.
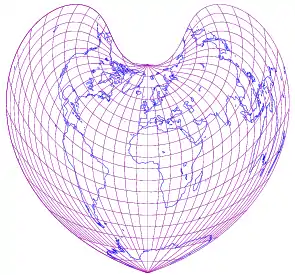
L'impossibilité de projeter le globe terrestre sur une surface plane sans distorsion (Theorema egregium) explique que diverses projections aient été inventées, chacune ayant ses avantages. Le choix d'une projection et le passage d'une projection à une autre comptent parmi les difficultés mathématiques que les cartographes ont dû affronter. L'informatique a apporté des outils de calcul puissants pour traiter ces problèmes.
Terminologie
Le terme de projection ne doit pas être compris dans le sens de projection géométrique (projection centrale ou perspective, projection orthogonale) mais comme une transformation mathématique faisant correspondre des points du globe et des points du plan. Il est probable que le terme de projection ait été utilisé en référence aux premières représentations planes (stéréographique ou gnomonique) qui sont effectivement des projections centrales.
Cette référence à une transformation géométrique est souvent source d'erreur. C'est pourquoi, le terme, trompeur, de «projection cartographique» est parfois remplacé par celui de «transformation plane»[1] ou «représentation plane»[2].
Description
D'un point de vue mathématique, une projection permet d'établir entre la surface de la Terre et le plan (ou la surface développable) une correspondance telle que :
et
où désignent des coordonnées planes, la latitude, la longitude et des fonctions qui sont continues partout sur l'ensemble de départ sauf sur un petit nombre de lignes et de points (tels que les pôles). Il existe donc une infinité de solutions. Les mathématiciens ne se sont pas privés d'en trouver, et on en connaît plus de 200[3].
De la Terre à la carte
La Terre a une forme irrégulière. Une projection s'appuie sur une sphère ou un ellipsoïde de révolution qui sont des modèles plus ou moins proches de la forme patatoïde réelle. On commence par choisir, à partir de son géoïde global, un ellipsoïde de révolution représentatif. Il existe plusieurs ellipsoïdes en usage, dont les plus courants sont :
- Clarke 1866
- Clarke 1880 anglais
- Clarke 1880 IGN
- Bessel
- Airy
- Hayford 1909
- International 1924
- WGS 66
- International 1967
- WGS 72
- IAG-GRS80
- WGS 84
Les ellipsoïdes IAG-GRS80 et WGS84 sont pour la plupart des applications à considérer comme étant identiques. Plus rigoureusement, l'écart en termes de demi-petit axe entre les ellipsoïdes WGS84 et IAG-GRS80 est de 0,1 mm. IAG-GRS80 est l'ellipsoïde mis en place en 1980 par l'International Association of Geodesy comme Geodetic Reference System.
WGS84 signifie World Geodetic System, créé en 1984.
L'ellipsoïde seul ne suffit pas : il est nécessaire de le positionner par rapport à la surface réelle de la Terre. La donnée de l'ellipsoïde et des paramètres de positionnement constitue ce qu'on appelle un datum géodésique à partir duquel pourra être appliquée une projection.
Un datum géodésique est donc défini par :
- la donnée de l'ellipsoïde ;
- la position du centre de l'ellipsoïde par rapport au centre de masse de la Terre (de quelques centimètres à plus d'une centaine de mètres) ;
- l'orientation des axes de l'ellipsoïde ;
ou, plus concrètement pour un datum local :
- l'ellipsoïde ;
- le point fondamental, où l'ellipsoïde tangente le géoïde,
- l'azimut initial (direction du nord en ce point),
- le méridien origine (du point de référence),
à quoi il convient d'ajouter la projection courante.
Il existe de nombreux datums, chacun adapté à un usage particulier, depuis des représentations globales du globe (ce sont les plus précises, comme DORIS qui permet de mesurer la dérive des continents ou le rebond post-glaciaire) jusqu'à des bases cadastrales (moins précises mais s'ajustant au plus près du géoïde). Voici quelques datums géodésiques en usage :
- Nouvelle triangulation de la France (NTF) : France (jusqu'en ; la plupart des cartes de l'IGN sont toujours dans ce système), basé sur l'ellipsoïde Clarke 1880 IGN. Le point fondamental est au Panthéon à Paris. La projection courante est Lambert.
- Réseau géodésique français (RGF) 1993 : France, basé sur l'ellipsoïde IAG-GRS80, la projection associée est la projection Lambert93 (projection conique conforme). En , une série de 9 projections coniques conformes a été aussi proposée comme projections associées au RGF93. La nomenclature de ces projections est : CC42, CC43, CC44, CC45, CC46, CC47, CC48, CC49 et CC50. Chaque zone est centrée sur un parallèle de latitude ronde, allant du 42e au 50e degré de latitude nord avec une emprise de un degré de latitude de part et d'autre de ce parallèle.
- European Datum (ED) 50 : système européen unifié, basé sur l'ellipsoïde Hayford 1909. Le point fondamental est à Potsdam, en Allemagne. La projection courante est UTM.
- World Geodetic System (WGS84) : système mondial (pas de point fondamental), mis au point par le Département de la Défense des États-Unis et utilisé par le GPS, basé sur l'ellipsoïde WGS84. La projection courante est UTM.
Les types de projections

Une fois un ellipsoïde fixé, on peut choisir le type de projection à appliquer pour obtenir une carte. Cette fois encore, ce choix est conduit par l'usage qui sera fait de la carte mais aussi de la position de la région à cartographier sur le globe.
Classification par les conservations
Les projections peuvent avoir diverses propriétés :
- projection équivalente : conserve les aires. Cette représentation est préférée dans les atlas[4] pour respecter les surfaces relatives des différents pays;
- projection conforme : conserve localement les angles, donc les formes. La topographie et la géodésie utilisent exclusivement ce type de représentation[4]. C'est les cas, par exemple, des cartes IGN[5] et des cartes marines;
- projection aphylactique : elle n'est ni conforme ni équivalente, mais peut être équidistante, c'est-à-dire conserver les distances sur les méridiens. Elle est utilisée, par exemple, comme compromis entre les représentations conformes et équivalentes pour minimiser les déformations induites par celles-ci[6]. Les cartes anciennes (projection cylindrique équidistante, projection de Cassini,...) utilisaient souvent la propriété d'équidistance.
Une projection ne peut pas être à la fois conforme et équivalente.
L'utilisation de l'indicatrice de Tissot permet d'apprécier le degré de conservation ou de déformation des formes ou des aires.
Classification par le canevas
Un point du globe étant repéré par sa longitude et sa latitude, une représentation cartographique est caractérisée par l'image des méridiens et des parallèles, c'est-à-dire le canevas de la carte. Les projections cartographiques sont donc également classifiées selon la forme de leur canevas[4]. Certains de ces canevas ont des formes voisines de celles obtenues par projection géométrique sur des surfaces développables (surfaces qui peuvent être étalées sans déformation sur un plan). Les trois surfaces développables les plus courantes, le plan, le cylindre et le cône), donnent lieu aux trois types principaux de projections :
- la projection cylindrique ;
- la projection conique ;
- la projection azimutale.
Une projection qui ne peut être classée dans un de ces types est appelée individuelle ou unique.
Projection cylindrique

Dans la projection cylindrique directe ou normale, le canevas ressemble à celui qui serait obtenu par projection géométrique sur un cylindre d'axe Nord-Sud.
- Les méridiens sont représentés par des droites parallèles équidistantes;
- les parallèles sont représentés par des droites perpendiculaires aux images des méridiens mais à distances variables.
C'est la trame des parallèles qui va différencier les différentes projections cylindriques. La trame associée à la projection centrale n'offre pas d'intérêt cartographique et n'a pas donné lieu à des cartes utilisables.
On distingue, parmi ces projections cylindriques celles dans lesquelles les déformations sont minimales à l'équateur, comme si on projetait sur un cylindre tangent à l'équateur (projection cylindrique tangente) et celles pour lesquelles les déformations sont minimales autour de deux parallèles (projection cylindrique sécante).
Il est parfois intéressant de construire un autre système de repérage sur le globe, constitué de pseudo-méridiens et de pseudo-parallèles, en choisissant sur le globe un autre axe principal que l'axe Nord-Sud[7]. La représentation plane de ces pseudo-méridiens et pseudo-parallèles définit un autre canevas. Quand ce canevas est constitué de pseudo méridiens parallèles et équidistants et de pseudo-parallèles perpendiculaires aux pseudo-méridiens, on parle de projection cylindrique
- transverse, si l'axe passe par deux points de l'équateur;
- oblique si l'axe ne passe ni par les pôles, ni par deux points de l'équateur.
Dans ces deux cas, le canevas des méridiens et des parallèles n'est plus un quadrillage de droites orthogonales. Par exemple, dans la projection cylindrique transverse, seuls l'équateur et un méridien sont transformés en deux droites perpendiculaires.
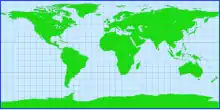
Exemples de projection cylindrique :
- Projection de Mercator (conforme)
- Projection de Peters (équivalente)
- Projection de Robinson (pseudo-cylindrique, aphylactique)
- Projection transverse universelle de Mercator (conforme) (aussi nommée UTM ou Projection de Gauss-Kruger)
- Projection MGRS
- Projection cylindrique équidistante
- Projection de Mercator oblique (utilisée en Suisse par exemple)
- Projection cylindrique de suivi des satellites, Space-oblique Mercator projection (en), de John Parr Snyder en 1987, où les traces au sol sont des droites[8],[9]
- Projection de Mollweide (pseudo-cylindrique)
Projection conique

Le canevas ressemble à celui qui serait obtenu par projection géométrique sur un cône de sommet situé sur l'axe Nord-Sud.
- Les méridiens sont représentés par des demi-droites concourantes formant entre elles un angle constant;
- Les parallèles sont représentés par des arcs de cercles concentriques.
C'est la trame des parallèles qui va distinguer les divers types de projections coniques.
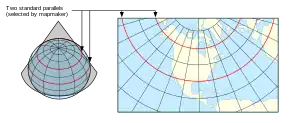
Comme pour les projections cylindriques, on distingue les projections coniques tangentes, où la déformation est minimale sur un parallèle et les projections coniques sécantes quand les déformations sont minimales autour de deux parallèles[10].
Exemples de projection conique :
Projection azimutale
C'est dans cette classe que l'on va rencontrer des projections vraies (centrales ou orthogonales) ou apparentées. On projette l'ellipsoïde sur un plan tangent en un point ou sécant en un cercle.
Il existe quatre types principaux de projections azimutales, qui se différencient par la position du centre utilisé pour la projection :
- projection stéréographique: le point de perspective est placé sur le sphéroïde ou l'ellipsoïde, sur le diamètre perpendiculaire au plan de projection ;
- projection gnomonique: le point de perspective est au centre du sphéroïde. La projection gnomonique conserve les orthodromies, puisque tout arc de grand cercle est projeté en un segment ;
- projection orthographique : Le point de perspective est à une distance infinie. On perçoit un hémisphère du globe comme si on était situé dans l'espace. Les surfaces et formes sont déformées, mais les distances sont préservées sur des lignes parallèles ;

Par ailleurs, selon la position du plan tangent, la projection azimutale est dite polaire (plan tangent à un pôle), équatoriale (plan tangent en un point de l'équateur), ou oblique (plan tangent en un autre point). La projection azimutale polaire sert pour les cartes représentant les lignes aériennes qui passent par les régions polaires afin de réduire la distance de parcours.
Exemples de projection azimutales
- projection azimutale équivalente de Lambert.
- Projection de Fuller (aussi appelée Dymaxion map) : projection gnomonique sur un polyèdre : cuboctaèdre (14 faces, 8 triangles équilatéraux et 6 carrés) ou plus souvent icosaèdre (20 triangles équilatéraux)
Projections uniques
Il existe de nombreuses cartes qui ne résultent pas d'une projection sur un cône, un cylindre ou un plan :
- Projection de Bonne
- Projection sinusoïdale
- Projection de Sanson-Flamsteed : une projection sinusoïdale découpée et redressée
- Projection de Goode : projection interrompue
- Projection de Winkel-Tripel : mélange entre deux projections
- Projection Equal Earth : projection pseudo-cylindrique équivalente
Références
- Cuenin, R., 1972, Cartographie générale, 2 tomes, Eyrolles, Paris.
- Driencourt L. et Laborde J., 1932, Traité des projections géographiques ; 4 fascicules, éd. Hermann, Paris.
- Dufour, J.-P., 2001, Introduction à la géodésie, Hermès, 334p.
- Gambier, G., 1984, Notions sur les représentations planes de la Terre, 114 p.
- (en) Hooijberg, M., 1997, Practical geodesy using computers, Springer Verlag, 308p.
- (en) Iliffe, J. C., 2002, Datum and map projections for remote sensing, GIS and surveying, Whittles Publishing, UK, 150 pp.
- Joly, F., 1985, La cartographie, collection Que sais-je ?, PUF, No 937, 127p.
- Levallois, J.-J., 1970, Géodésie générale - Tome 2 : Géodésie classique bidimensionnelle, éd. Eyrolles, 408p.
- Le Fur, A., 2004, Pratiques de la cartographie, éd. Armand Colin, 96p.
- Radix, J.-C., 1991, Répertoire géodésique en vue de la navigation, Éditions Cépaduès, Toulouse, 756p.
- Reignier, F., 1957, Les systèmes de projection et leurs applications, édition IGN, Saint-Mandé.
- (en) Snyder, J. P., 1987, Map projections - a working manual, USGS Paper 1935, Washington. 383p.
- (en) Snyder, J. P., 1997, Flattening the Earth: Two Thousand Years of Map Projections., University of Chicago Press, 384p. (ISBN 978-0-2267-6747-5)
- (en) Yang, Q., J. P. Snyder et W. R. Tolber, 2000, Map projection transformation, principles and applications, Taylor et Francis Editor, 367p.
- Françoise Duquenne et Henri Duquenne, Cours de géodésie, géodésie géométrique, École supérieure des géomètres et topographes, (lire en ligne), chapitre3, «Géodésie géométrique»
Notes
- Patrick Sillard, Les projections et référentiels cartographiques, École nationale des sciences géographiques, sept. 2000, p. 15
- Duquenne 1998, p. 10.
- Joly, 1985, page 39
- Duquenne 1998, p. 14.
- « Les projections, de Mercator au GPS », IGN magazine, no 5, , p. 4-5 (lire en ligne)
- Voir quelques exemples dans (en) « Radical cartography », WALL MAPS OF THE WORLD
- Duquenne 1998, p. 15-16.
- [PDF] « Cylindrical Satellite-tracking projection »
- (en) Mei-Ling Hsu, Philip M. Voxland, « Showing Routes for Globe Circlers »
- Duquenne 1998, p. 17.
Voir aussi
Articles connexes
Liens externes
- Dana, P., 1999, Cours en anglais avec de nombreuses figures: sur les projections cartographiques
- Sillard, P., 2000, Les projections et référentiels cartographiques, 61 pp.
- Weger, G., 1999, Sémiologie graphique et conception cartographique, volume 1, 141 pp
- Serveur éducatif consacré à l'information géographique
- Extrait d'un travail académique (Lycée Fustel, Coulanges, Académie de Strasbourg) sur les projections cartographiques
- F. de Labachelerie, C. Geoffroy, M. Magnenet, A. Parmentelat, De la shère au plan, Bulletin de l'IREM de Besançon N° 69 (nov. 2003)
- Étude des projections usuelles par l'ENMM du Havre
- (en) Eric W. Weisstein, « Map Projections », sur MathWorld
- (en) The Casual Cartographer : une série d'articles sur les projections et des programmes de conversion
- « Pourquoi les cartes géographiques sont mensongères », sur www.lemonde.fr, (consulté le ).
- [PDF] « Quels sont les différents modèles d’ellipsoïdes utilisés en France? », sur ign.fr, service de géodésie.
- (en) « Radical cartography » (Tableau d'exemples et propriétés de presque toutes les projections communes)
- Portail de la géométrie
- Portail de la cartographie
