Tétration

Afin de généraliser le premier cas ci-dessus (calcul des puissances de la droite vers la gauche) de la tétration à des valeurs non entières, une nouvelle notation est nécessaire. Le second cas (calcul de la gauche vers la droite) peut être également écrit : ${\displaystyle \left(\left(2^{2}\right)^{2}\right)^{2}=2^{2\times 2\times 2}=2^{2^{3}}}$, donc l'écriture de sa forme générale utilise toujours une notation d'exponentiation ordinaire.

Les notations dans lesquelles une tétration peut être notée (parmi celles permettant même des niveaux d'itérations plus élevés) incluent :

• la notation standard : ^ba, utilisée en premier lieu par Hans Maurer[1] ; cette notation a été popularisée par le livre de Rudy Rucker, Infinity and the Mind.
• la notation des puissances itérées de Knuth : ${\displaystyle a\uparrow \uparrow b}$ — peut être étendue en utilisant plus de flèches (ou de manière équivalente, une flèche indexée).
• la notation des flèches chaînées de Conway : ${\displaystyle a\rightarrow b\rightarrow 2}$ — peut être étendue en augmentant le nombre 2 (équivalentes avec les extensions au-dessus), mais aussi, de manière plus performante, en étendant la chaîne.
• la notation hyper4 : ${\displaystyle a^{(4)}b=\operatorname {hyper4} (a,b)=\operatorname {hyper} (a,4,b)}$ — peut-être étendue en augmentant le nombre 4 ; cela donne la famille des hyper opérateurs.

Le cas particulier a = 2 peut s'écrire avec la fonction d'Ackermann :

${\displaystyle 2\uparrow \uparrow b=\operatorname {A} (4,b-3)+3}$,

c.-à-d. ${\displaystyle \operatorname {A} (4,n)=2\uparrow \uparrow (n+3)-3}$.

La flèche vers le haut est utilisée de manière identique au signe d'omission, ce qui fait que l'opérateur tétration peut être écrit comme ^^ en ASCII : a^^b.

Pour un nombre réel a > 0 et un entier naturel n, on définit ${\displaystyle ^{n}a=a\uparrow \uparrow n}$ par récurrence :

${\displaystyle ^{0}a=a\uparrow \uparrow 0=1}$ ;

${\displaystyle ^{n+1}a=a\uparrow \uparrow (n+1)=a^{a\uparrow \uparrow n}}$.

(Les exemples écrits avec virgule sont approchés)

n = n↑↑1	n↑↑2	n↑↑3	n↑↑4
1	1	1	1
2	4	16	65 536
3	27	7,63×1012	${\displaystyle 10^{3{,}64\times 10^{12}}}$
4	256	1,34 × 10154	${\displaystyle 10^{8{,}07\times 10^{153}}}$
5	3 125	1,91 × 102 184	${\displaystyle 10^{1{,}34\times 10^{2\,184}}}$
6	46 656	2,70 × 1036 305	${\displaystyle 10^{2{,}07\times 10^{36\,305}}}$
7	823 543	3,76 × 10695 974	${\displaystyle 10^{3{,}18\times 10^{695\,974}}}$
8	16 777 216	6,01 × 1015 151 335	${\displaystyle 10^{5{,}43\times 10^{15\,151\,335}}}$
9	387 420 489	4,28 × 10369 693 099	${\displaystyle 10^{4{,}09\times 10^{369\,693\,009}}}$
10	10 000 000 000	1010 000 000 000	${\displaystyle 10^{10^{10^{10}}}}$

En utilisant la relation ${\displaystyle n\uparrow \uparrow k=\log _{n}\left(n\uparrow \uparrow (k+1)\right)}$ (déduite de la définition de la tétration), on peut définir les valeurs pour ${\displaystyle n\uparrow \uparrow k}$ pour ${\displaystyle k\in \{-1,0,1\}}$.

${\displaystyle {\begin{matrix}n\uparrow \uparrow 1&=&\log _{n}\left(n\uparrow \uparrow 2\right)&=&\log _{n}\left(n^{n}\right)&=&n\log _{n}n&=&n\\n\uparrow \uparrow 0&=&\log _{n}\left(n\uparrow \uparrow 1\right)&=&\log _{n}n&&&=&1\\n\uparrow \uparrow -1&=&\log _{n}\left(n\uparrow \uparrow 0\right)&=&\log _{n}1&&&=&0\end{matrix}}}$

Cela confirme la définition intuitive de ${\displaystyle n\uparrow \uparrow 1}$ comme étant simplement n. Cependant, on ne peut plus définir plus de valeurs par itération supplémentaire de cette manière, puisque ${\displaystyle n\uparrow \uparrow -2=\log _{n}(n\uparrow \uparrow -1)=\log _{n}0}$ n'est pas défini.

${\displaystyle 1\uparrow \uparrow n}$ peut être défini sans problème comme étant égal à 1. Puisque ${\displaystyle \log _{1}x}$ est indéfini (${\displaystyle \log _{1}x={\begin{matrix}{\frac {\log x}{\log 1}}\end{matrix}}}$), la définition donnée ci-dessus ${\displaystyle n\uparrow \uparrow {-1}=\log _{n}(n\uparrow \uparrow 0)}$ ne peut être utilisée lorsque n = 1 et ${\displaystyle 1\uparrow \uparrow {-1}}$ doit rester une quantité non définie.

Parfois, 0⁰ est considéré comme quantité indéfinie. Dans ce cas, les valeurs pour ${\displaystyle 0\uparrow \uparrow k}$ peuvent être définies par la limite ${\displaystyle \lim _{x\rightarrow 0}x\uparrow \uparrow k}$ qui existe et vaut :

${\displaystyle \lim _{x\rightarrow 0}x\uparrow \uparrow k={\begin{cases}1&{\mbox{ pour }}k{\mbox{ pair}}\\0&{\mbox{ pour }}k{\mbox{ impair}}\end{cases}}}$

${\displaystyle 0\uparrow \uparrow k}$ peut être définie en termes de cette limite et est en accord avec la définition de ${\displaystyle 0^{0}=1}$.

Représentation graphique de la fonction ${\displaystyle {\begin{aligned}f_{n}(x)&={}^{n}\!x\end{aligned}}}$ pour de petites valeurs de n.

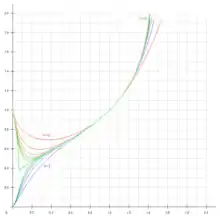
L'extension de ${\displaystyle x\uparrow \uparrow b}$ aux nombres réels ${\displaystyle x>0}$ est relativement simple et donne, pour chaque nombre entier naturel n, une fonction super-puissance ${\displaystyle \operatorname {f} _{n}(x)=x\uparrow \uparrow n}$ (le préfixe super est parfois remplacé par hyper : fonction hyper-puissance).

Comme indiqué précédemment, pour les entiers positifs n, la fonction tend vers 1 pour x tendant vers 0 si n est pair, et vers 0 si n est impair, alors que pour ${\displaystyle n=0}$ et ${\displaystyle n=-1}$, la fonction est constante, avec pour valeur 1 et 0, respectivement.

Puisqu'un nombre complexe peut être élevé à une puissance complexe en utilisant la branche principale du logarithme complexe, la tétration peut être appliquée aux nombres de la forme ${\displaystyle a+b\,\mathrm {i} }$, dans lesquels i est l'unité imaginaire.

Ainsi, calculons, par exemple, ${\displaystyle z\uparrow \uparrow k}$ dans lequel ${\displaystyle z=\mathrm {i} }$. L'exponentiation est effectuée en utilisant la branche principale du logarithme complexe, et l'on a la relation :

${\displaystyle \mathrm {i} ^{a+b\mathrm {i} }=\mathrm {e} ^{{\mathrm {i} \pi \over 2}(a+b\mathrm {i} )}=\mathrm {e} ^{-{b\pi \over 2}}\left(\cos {a\pi \over 2}+\mathrm {i} \sin {a\pi \over 2}\right)}$

Ce qui suggère une définition par récurrence pour ${\displaystyle \mathrm {i} \uparrow \uparrow (k+1)=a'+b'\,\mathrm {i} }$ lorsque ${\displaystyle \mathrm {i} \uparrow \uparrow k=a+b\,\mathrm {i} }$ :

${\displaystyle a'=\mathrm {e} ^{-{b\pi \over 2}}\cos {a\pi \over 2}}$

${\displaystyle b'=\mathrm {e} ^{-{b\pi \over 2}}\sin {a\pi \over 2}}$

On en déduit les valeurs approchées suivantes (${\displaystyle \mathrm {i} \uparrow z}$ est l'exponentiation ${\displaystyle \mathrm {i} ^{z}}$). :

• ${\displaystyle \mathrm {i} \uparrow \uparrow 1=\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 2=\mathrm {i} \uparrow \left(i\uparrow \uparrow 1\right)\approx 0{,}2079}$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 3=\mathrm {i} \uparrow \left(i\uparrow \uparrow 2\right)\approx 0{,}9472+0{,}3208\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 4=\mathrm {i} \uparrow \left(i\uparrow \uparrow 3\right)\approx 0{,}0501+0{,}6021\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 5=\mathrm {i} \uparrow \left(i\uparrow \uparrow 4\right)\approx 0{,}3872+0{,}0305\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 6=\mathrm {i} \uparrow \left(i\uparrow \uparrow 5\right)\approx 0{,}7823+0{,}5446\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 7=\mathrm {i} \uparrow \left(i\uparrow \uparrow 6\right)\approx 0{,}1426+0{,}4005\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 8=\mathrm {i} \uparrow \left(i\uparrow \uparrow 7\right)\approx 0{,}5198+0{,}1184\,\mathrm {i} }$
• ${\displaystyle \mathrm {i} \uparrow \uparrow 9=\mathrm {i} \uparrow \left(i\uparrow \uparrow 8\right)\approx 0{,}5686+0{,}6051\,\mathrm {i} }$

La résolution de la relation ${\displaystyle \mathrm {i} \uparrow \uparrow (k+1)=\mathrm {i} \uparrow (\mathrm {i} \uparrow \uparrow k)}$ conduit aux relations attendues ${\displaystyle \mathrm {i} \uparrow \uparrow 0=1}$ et ${\displaystyle \mathrm {i} \uparrow \uparrow -1=0}$.

Dans le plan complexe, la suite ${\displaystyle \mathrm {i} \uparrow \uparrow n}$ converge en spirale (voir infra). De telles suites de tétration ont été étudiées depuis l'époque d'Euler[2] mais sont très peu comprises en raison de leur comportement chaotique. Les recherches les plus publiées se sont historiquement concentrées sur la convergence de la fonction de tour de puissances. La recherche actuelle a grandement bénéficié du progrès de puissantes stations de calcul avec des supports logiciel en mathématiques symboliques et fractales. La plupart de ce qui est connu sur la tétration vient de la connaissance générale de la dynamique complexe et de la recherche spécifique sur les nappes exponentielles.

À ce jour, il n'existe pas de solution communément acceptée pour le problème général d'extension de la tétration aux nombres réels et complexes, bien que cela soit un champ de recherche actif.

Considérons le problème de trouver une fonction super-exponentielle ou une fonction hyper-exponentielle

${\displaystyle \operatorname {f} (x)=a\uparrow \uparrow x}$

qui est une extension au réel ${\displaystyle x>-2}$ de ce qui est défini précédemment, et qui satisfait :

• ${\displaystyle a\uparrow \uparrow (x+1)=a^{\left(a\uparrow \uparrow x\right)}}$ ;
• f est croissante (pour ${\displaystyle a>1}$) ;
• f est continue.

Graphes des fonctions ${\displaystyle f(x)=\,^{x}\mathrm {a} }$ définies en utilisant une interpolation affine entre − 1 et 0.

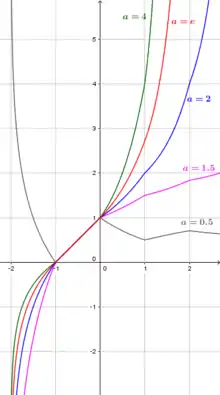
Lorsque ${\displaystyle x\mapsto a\uparrow \uparrow x}$ est définie sur un intervalle de longueur unitaire, on peut définir la fonction dans son ensemble pour tout ${\displaystyle x>-2}$, par récurrence.

Une solution simple est donnée par l'interpolation affine entre − 1 et 0 :

${\displaystyle a\uparrow \uparrow x=x+1}$ pour ${\displaystyle -1\leqslant x\leqslant 0}$,

par conséquent :

${\displaystyle \,\!a\uparrow \uparrow x=\log _{a}{(x+1)}}$ pour ${\displaystyle -2<x\leqslant -1}$

${\displaystyle a\uparrow \uparrow x=a^{x}}$ pour ${\displaystyle 0\leqslant x\leqslant 1}$,

${\displaystyle \,\!a\uparrow \uparrow x=a^{a^{(x-1)}}}$ pour ${\displaystyle 1<x<2}$

${\displaystyle \,\!a\uparrow \uparrow x=a^{a\uparrow \uparrow {(x-1)}}}$ pour ${\displaystyle x>2}$, etc.

Cependant, si a ≠ e, la fonction ainsi définie est seulement dérivable par morceaux : à des valeurs entières de x, la dérivée est multipliée par ${\displaystyle \ln a}$ entre deux intervalles :

${\displaystyle 10\uparrow \uparrow 0{,}99=9{,}77}$,

${\displaystyle 10\uparrow \uparrow 1=10}$,

${\displaystyle 10\uparrow \uparrow 1{,}01=10{,}55}$.

D'autres fonctions, plus compliquées, peuvent être plus régulières ou satisfont des propriétés additionnelles (fonction analytique, ou fonction prolongeable en une fonction holomorphe, etc.).

Une fonction super-exponentielle croît plus vite qu'une fonction exponentielle double.

Par exemple, si a = 10 :

• ${\displaystyle \operatorname {f} (-1)=0}$
• ${\displaystyle \operatorname {f} (0)=1}$
• ${\displaystyle \operatorname {f} (0{,}3)\approx 2}$
• ${\displaystyle \operatorname {f} (1)=10}$
• ${\displaystyle \operatorname {f} (1{,}3)\approx 10^{2}}$
• ${\displaystyle \operatorname {f} (2)=10^{10}}$
• ${\displaystyle \operatorname {f} (2{,}3)\approx 10^{100}}$ (googol)
• ${\displaystyle \operatorname {f} (3)=10^{10^{10}}}$
• ${\displaystyle \operatorname {f} (3{,}3)\approx 10^{10^{100}}}$ (googolplex)

Lorsque l'on définit ${\displaystyle a\uparrow \uparrow x}$ pour tout a, une autre condition requise peut être que ${\displaystyle a\uparrow \uparrow x}$ est croissante avec a.

Les fonctions réciproques de la tétration relativement à la base ou relativement au deuxième opérande sont appelées respectivement super-racines ou hyper-racines, et super-logarithme ou hyper-logarithme.

La bijection réciproque de la fonction super-exponentielle ${\displaystyle \operatorname {f} (x)=a\uparrow \uparrow x}$ est définie, si a > 1, pour tous les nombres réels, y compris les nombres négatifs.

La fonction super-logarithme ${\displaystyle \mathrm {slog} _{a}}$ vérifie :

${\displaystyle \mathrm {slog} _{a}(a\uparrow \uparrow x)=\mathrm {slog} _{a}(^{x}a)=x}$

${\displaystyle a\uparrow \uparrow (\mathrm {slog} _{a}x)=^{\mathrm {slog} _{a}x}a=x}$

${\displaystyle \mathrm {slog} _{a}1=0}$

${\displaystyle \mathrm {slog} _{a}a=1}$

${\displaystyle \mathrm {slog} _{a}0=-1}$

${\displaystyle \mathrm {slog} _{a}a^{x}=1+\mathrm {slog} _{a}x}$

${\displaystyle \mathrm {slog} _{a}x=-1+\mathrm {slog} _{a}a^{x}}$

${\displaystyle \mathrm {slog} _{a}x=1+\mathrm {slog} _{a}\log _{a}x\,}$ si x > 0

${\displaystyle \mathrm {slog} _{a}x>-2}$

Dans le paragraphe précédent on a défini :

${\displaystyle a\uparrow \uparrow x=x+1}$ pour ${\displaystyle -1<x<0}$,

${\displaystyle a\uparrow \uparrow x=a^{x}}$ pour ${\displaystyle 0<x<1}$,

Par conséquent (avec a > 1)

${\displaystyle \mathrm {slog} _{a}x=\log _{a}x,\,}$ si ${\displaystyle \,1<x\leqslant a}$ (on interpole par une fonction logarithme entre 1 et a) :

${\displaystyle \mathrm {slog} _{a}x=-1+x,\,}$ si ${\displaystyle \,0<x\leqslant 1}$ (on interpole par une fonction affine entre 0 et 1) :

${\displaystyle \mathrm {slog} _{a}x=-1+\mathrm {slog} _{a}a^{x}=-2+a^{x},\,}$ si ${\displaystyle x\leqslant 0}$.

Exemples :

• ${\displaystyle \mathrm {slog} _{10}3=\log _{10}3\approx 0{,}477}$ ;
• ${\displaystyle \mathrm {slog} _{10}10^{-3}=-1+10^{-3}=-0{,}999}$ ;
• ${\displaystyle \mathrm {slog} _{10}(-3)=-1+\mathrm {slog} _{10}10^{-3}=-1+(-0{,}999)=-1{,}999}$ ;
• ${\displaystyle \mathrm {slog} _{10}10^{6\times 10^{23}}=1+\mathrm {slog} _{10}(6\times 10^{23})\approx 2+\mathrm {slog} _{10}23{,}778\approx 3+\mathrm {slog} _{10}1{,}376=3+\log _{10}1{,}376\approx 3{,}139}$.

Graphe de la fonction ${\displaystyle f(x)={^{\infty }}x}$.

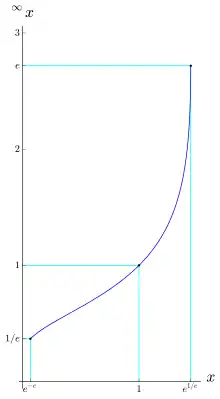
La suite ${\displaystyle {\sqrt {2}}\uparrow \uparrow n={\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\;.^{\;.^{\;.}}}}}}}$ converge vers 2. La tendance vers 2 peut être perçue en évaluant une petite tour finie :

${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1{,}41}}}}}\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1{,}63}}}}\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1{,}76}}}\approx {\sqrt {2}}^{{\sqrt {2}}^{1{,}84}}\approx {\sqrt {2}}^{1{,}89}\approx 1{,}93}$.

En général, la tour de puissances ${\displaystyle \left(^{n}x\right)}$ converge si, et seulement si[3]^,[4], ${\displaystyle \mathrm {e} ^{-\mathrm {e} }\leq x\leq \mathrm {e} ^{1/\mathrm {e} }}$.

Pour un réel quelconque r avec ${\displaystyle \mathrm {e} ^{-1}\leq r\leq \mathrm {e} }$, si ${\displaystyle x=r^{1/r}}$, alors la limite ${\displaystyle ^{\infty }x=x^{x^{x^{..}}}}$ de ${\displaystyle \left(^{n}x\right)}$ est r.

La fonction ${\displaystyle x\mapsto r={^{\infty }x}}$ peut être étendue aux nombres complexes z avec la définition :

${\displaystyle ^{\infty }z=-{\frac {\mathrm {W} _{0}(-\operatorname {Log} z)}{\operatorname {Log} z}}}$ pour z ≠ 1,

où ${\displaystyle \mathrm {W} _{0}}$ est la branche principale de la fonction W de Lambert et Log est celle du logarithme complexe.

Par exemple[5] :

${\displaystyle ^{\infty }\mathrm {i} ={\frac {2\mathrm {i} }{\pi }}\;W_{0}\left(-{\frac {\pi \mathrm {i} }{2}}\right)}$ ≈ 0,4383 + 0,3606 i (suites  A077589 et  A077590 de l'OEIS), de module ${\displaystyle {\frac {2}{\pi }}\left|W_{0}\left(-{\frac {\pi \mathrm {i} }{2}}\right)\right|}$ ≈ 0,567 555 ( A212479).