Trompette de Gabriel
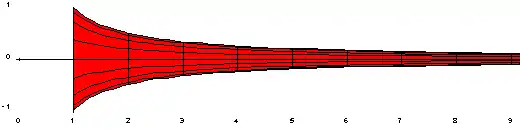
La trompette de Gabriel ou solide hyperbolique aigu est une surface de révolution, définie en faisant tourner une portion d'hyperbole autour d'une de ses asymptotes, et en la coupant par un plan orthogonal à l'axe.

Cette figure a été inventée vers 1640, par Evangelista Torricelli qui démontre que son volume est fini, bien que sa longueur soit infinie (sa surface latérale l'est également). Ce résultat a eu beaucoup de retentissement au 17e siècle, parmi les mathématiciens d'abord, puis chez les philosophes et les épistémologues, tant le paradoxe semblait insaisissable. Cette diffusion s'inscrit dans un moment charnière de l'histoire des mathématiques, marquant la transition entre une géométrie fidèle à la tradition antique et les concepts modernes. Cette transition nécessite une formalisation rigoureuse de deux notions : la calcul infinitésimal et l'infini. Le paradoxe posé par la trompette de Gabriel contribue à l'avancée sur ces deux plans.
A l'époque contemporaine, cette figure reste présente dans de nombreux manuels, comme exercice de calcul infinitésimal. Différents noms lui sont donnés : cor de Gabriel, trompette de Torricelli, chapeau du magicien, etc.
Généralités
La trompette de Gabriel est engendrée par une portion d'hyperbole d'équation
- ,
tracée sur l'intervalle et tournant autour de l'axe (Ox)[1]. Une définition un peu plus générale utilise l'hyperbole sur l'intervalle et conserve les mêmes propriétés[2].
Calcul du volume
Son volume est obtenu en intégrant la surface (surface normale à l'axe 0x à l'ordonnée x). On montre très facilement qu'il est égal à π[1] :
Calcul de l'aire
Et l'aire de la portion de trompette entre et est donnée par la formule suivante, selon le premier théorème de Guldin[1] :
Qui peut se minorer facilement, en remarquant que le contenu de la racine carrée est toujours strictement supérieur à 1 :
est strictement supérieur à une expression qui diverge quand tend vers , donc tend lui-même vers l'infini.
Paradoxe du peintre
Une façon d'exprimer le paradoxe d'avoir un solide de volume fini et de surface infinie est la question suivante : serait-il possible de peindre la surface intérieure de la trompette de Gabriel? Si on raisonne à partir de la surface, celle-ci étant infinie, l'opération semble impossible : il faudrait une quantité infinie de peinture. Mais d'autre part, il est possible de remplir intégralement la trompette avec un volume fini de peinture, ce qui, a priori, recouvre toute sa surface. Le paradoxe s'explique en s'interrogeant sur l'épaisseur de la peinture. En faisant le raisonnement « une surface infinie demande une quantité infinie de peinture », on suppose que la peinture a une épaisseur donnée, non nulle (qui devient supérieure au rayon de la trompette, quand dépasse ). Si on imagine une peinture « mathématique » d'épaisseur nulle, alors le volume de peinture devient une forme indéterminée de type [3].
Centre de gravité
Une autre propriété surprenante de la trompette de Gabriel, pointée dès le XVIIe siècle, est l'inexistence d'un centre de gravité[2]. Le centre de gravité du solide de révolution généré par la courbe se trouve, par symétrie, sur l'axe, seule son abscisse doit être calculée, elle est donnée par la formule suivante[4] :
Appliquée à la trompette de Gabriel, cette formule n'a pas de solution, puisque l'intégrale au numérateur ne converge pas.
Contexte historique

Le mathématicien Nicole Oresme, au XIVe siècle, s'était beaucoup intéressé à la question de la convergence ou de la divergence des sommes d'un nombre infini de termes. Il en a proposé des représentations graphiques comme, ci-contre, cette figure qui a une hauteur et un périmètre infinis, tout en ayant une surface finie, égale à 2[5]. Cet antécédent n'est jamais cité dans le débat qui entoure la trompette de Gabriel trois siècles plus tard, il semble que cette partie des travaux d'Oresme était tombée dans l'oubli à cette époque[2].
Les mathématiques de la première moitié du XVIIe siècle sont marquées par de nombreuses tentatives de formaliser l'étude des infinis et des infiniment petits. Le dialogue de Galilée (1632) s'en fait par exemple l'écho. Les mathématiciens et les philosophes sont divisés sur la notion d'infini : a-t-elle un sens mathématique? Peut-on introduire une grandeur infini dans un calcul ? Existe-t-il plusieurs infinis différents?[6].
Vers 1630, Fermat introduit, pour chercher les extrémas d'un résultat mathématique (la notion même de fonction n'a pas encore été formalisée), une quantité qu'il rend de plus en plus petite puis qui disparait du calcul, c'est un premier pas vers le calcul infinitésimal, mais celui-ci ne sera formalisé qu'à la fin du siècle, par Newton et Leibniz[7].
Le débat sur la trompette de Gabriel s'incrit donc dans le développement de ces notions, et y contribue[8].
Les démonstrations de Torricelli
Torricelli énonce le théorème suivant :
Solidum acutum hyperbolicum, infinitè lungum, sectum plano ad axem erecto vnà cum cylindro suæ basis, æquale est cylindro cuidam recto, cuius basis diameter sit latus versum, siue axis hyperbolæ, altitudo verò sit æqualis semidiametro basis ipsius acutis solidi.
« Le solide hyperbolique aigu, infiniment long, coupé par un plan perpendiculaire à l'axe, ajouté à un cylindre de la même base, est égal [en volume] au cylindre dont la base est la section transverse de l'hyperbole, et dont la hauteur est égale au rayon de la base du solide. »
L'énoncé seul est déjà remarquable dans l'histoire des mathématiques. Torricelli pose clairement que l'objet qu'il étudie est de longueur infinie, et non « indéfinie » : ce n'est pas une valeur qu'on peut rendre arbitrairement grande, le solide n'a vraiment pas de fin. Il y a là, souligné explicitement par les explications de Torricelli dans les correspondances, la revendication d'une forme de liberté intellectuelle : le mathématicien s'autorise à étudier un objet qui, manifestement, ne pourra jamais être réalité en pratique, pas même de façon approchée[2].
Par méthode des indivisibles
La trompette de Gabriel est étudiée par Evangelista Torricelli qui l'appelle le « solide hyperbolique aigu » (solidum hyperbolicum acutum)[9]. Vers 1641, à une époque où le calcul intégral n'existe pas, il démontre que son volume est identique à celui d'un cylindre en utilisant la méthode des indivisibles développée par Bonaventura Cavalieri. Torricelli ne conçoit pas les indivisibles exactement de la même façon que Cavalieri : il leur attribue une épaisseur, petite devant les dimensions du solide, là où Cavalieri les conçoit comme des objets bidimensionnels. Cette évolution constitue un pas vers le calcul intégral. En quelque sorte, l'approche de Torricelli revient à s'imaginer que le solide est constitué d'un empilement de feuilles de papier, qu'il va réorganiser[2].
Lemme 1 : Par révolution de l'hyperbole apollonienne définie par autour de son asymptome, on obtient un solide de révolution infiniment long.
Lemme 2 : tous les cylindres inscrits dans le solide précédemment défini ont la même surface latérale.
Lemme 3 : tous ces cylindres ont une volume proportionnel au diamètre de leur base. En effet, le cylindre construit avec un rayon r (<1) a une hauteur , son volume vaut donc
Lemme 4 : Chacun de ces cylindres a une surface latérale égale au quart de la surface de la sphère de rayon Lemme 5 : Chacun de ces cylindres a une surface latérale égale à l'aire du disque de rayon
Pour cela, il complète la trompette par un « bouchon », c'est-à-dire un cylindre de rayon 1 et de hauteur 1 (donc de volume π), qui relie le plan Oyz et la base de la trompette. Il découpe ensuite son volume obtenu en cylindres coaxiaux d'épaisseur infinitésimale. Pour reprendre l'analogie, les feuilles de papiers successives ont été enroulées autour de l'axe des . Il déplie ces cylindres en rectangle. Chaque rectangle a pour dimensions , comme le produit est constant, tous les rectangles ont la même aire : 2π. Il déforme alors chaque rectangle en disque de même aire, donc de rayon . Il obtient ainsi un cylindre de hauteur 1 et de surface de base égale à , donc de volume égal à . Il lui suffit alors d'enlever le volume connu du «bouchon» pour trouver le volume de la trompette : . Au passage, le volume de la corne est égal à celui du « bouchon », ce qui est un autre résultat remarquable[8].
- Calcul du volume par Torricelli
.PNG.webp) étape 1.
étape 1..PNG.webp) étape 2.
étape 2..PNG.webp) étape 3.
étape 3.
Démonstration par exhausion
La validité de la méthode des indivisibles ne faisant pas l'unanimité, Torricelli double son calcul du volume par un raisonnement par exhaustion. Cette méthode est utilisée depuis Euclide et donc à même de rassurer les géomètres les plus conservateurs. Elle consiste à faire deux démonstrations par l'absurde, démontrant l'une que le volume ne peut pas être supérieur au résultat recherché, l'autre qu'il ne peut pas être inférieur. Cette méthode est rigoureuse, mais elle nécessite de connaitre déjà le résultat, elle est donc utilisée pour consolider une valeur obtenue par d'autres méthodes.
Retentissement
Correspondances entre mathématiciens
À partir de la fin 1641, Torricelli partage cette découverte avec d'autres mathématiciens, à commencer par Cavalieri, dont il fut élève.
Il double sa démonstration par un raisonnement par exhaustion. Roberval, par la suite, fournit une démonstration que Torricelli reconnait être plus ingénieuse[8].
Qu'un solide de longueur infinie puisse posséder un volume fini semble contre-intuitif aux mathématiciens de l'époque et suscite de nombreuses correspondances sur le sujet du fini et de l'infini[10]. Cavalieri s'en étonne, et Roberval met d'abord en doute le résultat de Torricelli[10].

Publication de l'Opera Geometrica
En 1644, Torricelli publie l'Opera geometrica, ouvrage imprimé de géométrie. Il y inclut un chapitre sur le solide hyperbolique aigu, et le paradoxe est ainsi diffusé bien au-delà du petit cercle de mathématiciens qui avait échangé sur le sujet jusque-là[8].
Réactions des contemporains
Ce résultat suscite l'admiration de Gassendi. Il remet en cause la définition du solide chez Barrow et Mersenne. Il inspire à Pascal cette réflexion : « Incompréhensible. Tout ce qui est incompréhensible ne laisse pas d'être. Le Nombre infini. Un espace infini égal au fini. »[8] Le père Pardies, dans la préface de ses Elemens de Geométrie en 1671, en fait une preuve de l'existence de Dieu[10]. Ce résultat déstabilise Descartes dans ses convictions sur l'infini et suscite un débat entre Hobbes et Wallis[10].
Variantes et généralisations
Gâteau de mariage de Gabriel

Le gâteau de mariage de Gabriel est une variante de la trompette. Elle remplace la fonction hyperbole par une fonction en paliers, qui pour x positif vaut :
Où E(x) dénote la partie entière. Le solide obtenu est donc un empilement infini de cylindres dont les rayons sont les inverses des entiers. La surface de cette figure se calcule en additionnant les surfaces latérales des cylindres, plus les parties verticales qui se complètent à l'infini en un cercle de rayon 1 : On retrouve donc la série harmonique, qui diverge, la surface est infinie.
Le volume est fini, il se calcule simplement en sommant la surface des cylindres de hauteur 1 et de rayon :
On retrouve, au facteur π près, la série du problème de Bâle, on a donc . Le gâteau de mariage de Gabriel, apporté en complément de la trompette, a une certaine valeur pédagogique, pour introduire les comparaisons entre sommes continues (intégrales) et sommes discrètes (séries)[11].
Changement de l'exposant
On peut généraliser quelque peu la trompette de Gabriel simplement en appliquant un exposant p au dénominateur. La fonction génératrice devient : Il se démontre alors, en écrivant sous forme d'intégrales le volume et la surface, que :
- La surface est finie si et seulement si
- Le volume est fini si et seulement si
Le paradoxe se retrouve donc, pour toute valeur p comprise dans l'intervalle [12].
Équivalents à longueur finie

Si la trompette de Gabriel n'est pas bornée en x, il existe des solides de révolution qui ont une surface infinie, un volume fini, et une longueur finie. Un tel objet est proposé par Mark Lynch en 2005. Il s'agit du solide de révolution généré par une fonction qui, à l'approche de 0, présente des oscillations de plus en plus petites en amplitude, mais d'une période de plus en plus courte[13]. La fonction utilisée par Lynch est définie par morceau. Une variante publiée en 2006 utilise une fonction continue et dérivable. Le volume est présenté ci-contre, de même qu'une partie de la fonction sur l'interval de 0 à 0,3. La fonction génératrice est :
, prolongée avec [14].
Dimensions supérieures
La corne de Gabriel peut se généraliser dans un hyperspace de dimension quelconque. Cette généralisation n'a été étudiée que dans les années 2000. Si une hyperbole de dimension n, générée par la fonction , est utilisée pour générer, par rotation autour de son asymptote, une hypersurface en dimension n+1, alors, on retrouve le paradoxe (hypersurface infinie et hypervolume fini), pour toute valeur de p vérifiant[1] :
Comparaison avec des problèmes similaires
Cissoïde
À la même époque, Huygens et Sluse, étudiant la cissoïde, prouvent l'existence d'un récipient de volume fini et pouvant contenir un volume infini. Il s'agit d'un « vase » obtenu par rotation de la surface comprise entre la cissoïde et son asymptote autour de l'axe parallèle à l'asymptote passant par le sommet de la cissoïde. Cette figure a parfois été présentée à tort comme la réciproque de la trompette de Gabriel, mais cette description est trompeuse, car on compare ici deux volumes, et non une surface et un volume[15].
Isopérimétrie
La véritable réciproque de la trompette de Gabriel serait un objet de surface finie englobant un volume infini, mais aucun objet de ce type n'existe (en géométrie euclidienne). il est même prouvé qu'un solide d'un volume donné a forcément une surface supérieure ou égale à celle de la sphère de même volume[16].
Fractales
Les objets à structure fractale présentent eux aussi des paradoxes comme celui d'une surface infinie pour un volume fini, mais arrivent à cette propriété en possédant une structure locale infiniment complexe. Des parallèles peuvent être établis avec la trompette de Gabriel : par exemple le Flocon de Koch présente le même paradoxe dit du peintre[17].
Notes et références
- (en) Vincent Coll et Michael Harrison, « Gabriel's Horn: A Revolutionary Tale », Mathematics Magazine, vol. 87, no 4, , p. 263–275 (ISSN 0025-570X, DOI 10.4169/math.mag.87.4.263, lire en ligne, consulté le )
- (en) Paolo Mancosu et Ezio Vailati, « Torricelli's Infinitely Long Solid and Its Philosophical Reception in the Seventeenth Century », Isis, vol. 82, no 1, , p. 50–70 (ISSN 0021-1753 et 1545-6994, DOI 10.1086/355637, lire en ligne, consulté le )
- (en) Michael Huemer, Approaching infinity, (ISBN 978-1-137-56087-2 et 1-137-56087-8, OCLC 950884501, lire en ligne), p. 183
- (en) Philip E. Protter, Calculus with analytic geometry., Jones and Bartlett, (ISBN 0-86720-093-6 et 978-0-86720-093-5, OCLC 16950243, lire en ligne)
- (en) Jeff Babb, « Mathematical Concepts and Proofs from Nicole Oresme: Using the History of Calculus to Teach Mathematics », Science & Education, vol. 14, nos 3-5, , p. 443–456 (ISSN 0926-7220 et 1573-1901, DOI 10.1007/s11191-004-7937-y, lire en ligne, consulté le )
- Jean-Baptiste Jeangène Vilmer, « La prudence de Descartes face à la question de l’infini en mathématiques », Philosophiques, vol. 34, no 2, , p. 295–316 (ISSN 0316-2923 et 1492-1391, DOI 10.7202/016991ar, lire en ligne, consulté le )
- Jacques Bair et Valérie Henry, « Les infiniment petits selon Fermat : prémisses de la notion de dérivée », Bibnum. Textes fondateurs de la science, (ISSN 2554-4470, lire en ligne, consulté le )
- Jean Itard, « La lettre de Torricelli à Roberval d'octobre 1643 », Revue d'histoire des sciences, vol. 28, no 2, , p. 113–124 (DOI 10.3406/rhs.1975.1131, lire en ligne, consulté le )
- « Solide hyperbolique aigu », dans Encyclopédie ou Dictionnaire universel raisonné des connoissances humaines, vol. 38, (lire en ligne), p. 752-753
- (en) Paolo Mancuso, Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century, (présentation en ligne), p. 136-149
- (en) Steven J. Kifowit et Terra A. Stamps, Prairie State College The harmonic series, (lire en ligne)
- (en) Roger B. Nelsen, College calculus : a one-term course for students with previous calculus experience, (ISBN 978-1-939512-06-2 et 1-939512-06-9, OCLC 897450412, lire en ligne)
- (en) Mark Lynch, « A Paradoxical Paint Pail », The College Mathematics Journal, vol. 36, no 5, , p. 402–404 (ISSN 0746-8342, DOI 10.2307/30044894, lire en ligne, consulté le )
- Joseph Krenicky et Jan Rychtář, « Notes on Gabriel's Horn », Furman University Electronic Journal of Undergraduate Mathematics, vol. 11, no 1, , p. 4–7 (lire en ligne, consulté le )
- (en) Frank Swetz, John Fauvel, Victor J. Katz, Otto Bekken, Bengt Johansson, Learn from the Masters !, MAA 1994, p 88.
- (en) Robert Osserman, « The isoperimetric inequality », Bulletin of the American Mathematical Society, vol. 84, no 6, , p. 1182–1238 (ISSN 0002-9904 et 1936-881X, lire en ligne, consulté le )
- (en) Rida Suraiya Khan, « The Painter’s Paradox comparative analysis of Gabriel’s Horn and triangular pipe with Koch’s Fractal shaped cross section », sur At Right Angles, (consulté le )
Voir aussi
- Portail de la géométrie