Normale (géométrie)

Dans le cas des courbes planes, une simple rotation de π/2 de la tangente donne la normale ; cette notion ne joue par conséquent qu'un rôle secondaire dans l'étude, sauf peut-être pour déterminer les centres de courbure.

Pour les courbes gauches, il y a une infinité de normales en chaque point, décrivant un plan orthogonal au vecteur tangent en ce point. On en privilégie une, celle située dans le plan osculateur ; le vecteur tangent, le vecteur normal correspondant, et leur produit vectoriel (appelé vecteur binormal) constituent le repère de Frenet, particulièrement important pour l'étude du comportement local des courbes paramétrées.

Fig. 1 : Un plan et deux vecteurs normaux.

Comme exemple de surface non fermée, on considère le plan P défini par son équation cartésienne :

${\displaystyle ax+by+cz+d=0}$.

En tout point A de P, un vecteur normal à P est ${\displaystyle {\vec {n}}={\begin{pmatrix}a\\b\\c\end{pmatrix}}}$. Ce vecteur est un vecteur directeur de la droite normale à P en A.

Puisqu'un plan n'est pas une surface fermée, les concepts d'extérieur et d'intérieur sont le résultat d'une convention et non d'une définition. Comme vecteur normal unitaire au plan P, on peut donc choisir :

${\displaystyle {\vec {n}}_{1}={\frac {1}{\sqrt {a^{2}+b^{2}+c^{2}}}}{\begin{pmatrix}a\\b\\c\end{pmatrix}}\quad }$ ou ${\displaystyle \quad {\vec {n}}_{2}=-{\frac {1}{\sqrt {a^{2}+b^{2}+c^{2}}}}{\begin{pmatrix}a\\b\\c\end{pmatrix}}}$.

Ces deux vecteurs ont même direction et même norme (égale à 1), mais ont des sens opposés (cf. Figure 1).

Fig. 2 : La normale à une surface en un point donné est identique à la normale au plan tangent à cette surface en ce point.

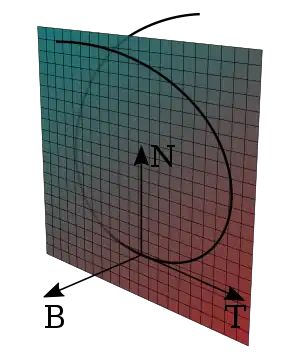
Soit une surface fermée S dans un espace euclidien de dimension trois. Pour trouver le vecteur normal unitaire (c'est-à-dire le vecteur unitaire de la droite normale à cette surface, orienté vers l'extérieur de S) en un point ${\displaystyle A(a_{1},a_{2},a_{3})}$, on utilise le produit vectoriel de deux vecteurs directeurs du plan tangent à S en A. Sur la Figure 2, la surface est représentée en rouge et le plan tangent en bleu.

Soit P ce plan tangent. Soient ${\displaystyle {\vec {u}}{\begin{pmatrix}u_{1}\\u_{2}\\u_{3}\end{pmatrix}}}$ et ${\displaystyle {\vec {v}}{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}}$ deux vecteurs directeurs de P. Le système d'équations paramétriques du plan tangent est alors :

${\displaystyle M(\lambda ,\mu )\quad {\begin{cases}x=a_{1}+\lambda u_{1}+\mu v_{1}\\y=a_{2}+\lambda u_{2}+\mu v_{2}\\z=a_{3}+\lambda u_{3}+\mu v_{3}\end{cases}}}$

Soit ${\displaystyle {\vec {w}}={\vec {u}}\wedge {\vec {v}}}$ le vecteur résultant du produit vectoriel de ${\displaystyle {\vec {u}}}$ et de ${\displaystyle {\vec {v}}}$. Par définition, ${\displaystyle {\vec {w}}}$ est un vecteur normal au plan tangent P. Le vecteur normal unitaire ${\displaystyle {\vec {n}}}$ est alors égal à :

${\displaystyle {\vec {n}}={\frac {\vec {w}}{\|{\vec {w}}\|}}}$.

Le sens de ce vecteur est clairement défini puisque l'extérieur d'une surface fermée est clairement défini.

Soit une surface définie par un paramétrage

${\displaystyle M(\lambda ,\mu )=\left(x(\lambda ,\mu ),y(\lambda ,\mu ),z(\lambda ,\mu )\right)}$

avec des fonctions x, y, z de classe C¹. Le point de paramètre (λ, μ) est dit régulier lorsque les vecteurs dérivés partiels en ce point sont indépendants. On peut alors former leur produit vectoriel

${\displaystyle N(\lambda ,\mu )={\frac {\partial M}{\partial \lambda }}(\lambda ,\mu )\wedge {\frac {\partial \mathrm {M} }{\partial \mu }}(\lambda ,\mu )}$

qui constitue un vecteur normal à la surface (non nécessairement unitaire).

Si la surface est donnée par une équation cartésienne f(x, y, z) = 0, avec une fonction f de classe ${\displaystyle {\mathcal {C}}^{1}}$, un point de la surface est dit régulier si le gradient de f est non nul en ce point. C'est alors le vecteur gradient lui-même qui constitue un vecteur normal :

${\displaystyle {\overrightarrow {\operatorname {grad} }}f{\begin{pmatrix}{\frac {\partial f}{\partial x}}\\{\frac {\partial f}{\partial y}}\\{\frac {\partial f}{\partial z}}\end{pmatrix}}}$

La démonstration formelle de ce résultat fait intervenir le théorème des fonctions implicites. Il est toutefois possible d'en donner une approche simplifiée à l'aide de la notion de « variations infinitésimales ».

En effet, si on se place en un point M(x, y, z) de la surface, sur son voisinage, la fonction f garde toujours la même valeur : 0. Par conséquent, sa variation infinitésimale lors d'un déplacement sur la surface défini par le vecteur ${\displaystyle {\vec {\mathrm {d} l}}=(\mathrm {d} x,\mathrm {d} y,\mathrm {d} z)}$ est nulle : df = 0.

Or, par définition du gradient, on a ${\displaystyle \mathrm {d} f={\overrightarrow {\operatorname {grad} }}(f)\cdot {\vec {\mathrm {d} l}}}$. Puisque ce produit scalaire est nul, le gradient en M est bien perpendiculaire à la surface en ce point.

En optique, la normale à un dioptre (surface séparant deux milieux) détermine la réflexion spéculaire et la réfraction parfaite (non diffuse, les deux phénomènes suivant les lois de Snell-Descartes).

En mécanique, lorsque deux pièces sont en contact, alors :

• le mouvement relatif entre les deux pièces est impossible suivant la normale ;
• si le contact est supposé parfaitement glissant (pas d'adhérence ni de frottement), la force de contact qu'exerce une pièce sur l'autre est selon la normale à la surface de contact.

La normale à la surface de contact est donc un élément important de la définition d'une liaison mécanique.

En imagerie informatique, et en particulier en modélisation tridimensionnelle, le fait de connaître le vecteur normal orienté à une facette permet :

• de déterminer si cette facette est visible ou bien cachée : dans le cas d'une surface délimitant un volume fermé, si la normale est orientée vers l'extérieur, alors la facette est visible si la normale pointe vers l'observateur (caméra virtuelle), cachée si elle pointe à l'opposé ;
• de déterminer l'éclairage de la facette, par les lois de l'optique (voir ci-dessus) ;
• d'effectuer un dégradé de couleurs : si l'on veut représenter une surface courbe et lisse, on est obligé, pour des raisons pratiques, de la découper en facettes planes, on peut atténuer l'effet de facettage en faisant un dégradé de couleur entre les facettes, la détermination de ce dégradé faisant intervenir les normales.