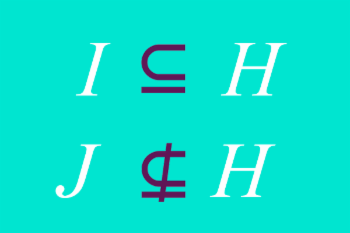Existen distintos dos tipos de relaciones entre conjuntos. En esta lección aprenderás la de contenencia.
Como te puedes dar cuenta, cada elemento que pertenece al conjunto `G`, pertenece también al conjunto `F`. Cuando se da esta situación decimos que un conjunto está contenido en el otro, o que es un subconjunto del otro.
En este caso `G` está contenido en `F`, o lo que es igual, `G` es subconjunto de `F`.
La manera correcta de representar la relación de contenencia es dibujar un conjunto dentro del otro. Para el caso de los conjuntos `F` y `G` definidos anteriormente, la representación correcta es como se muestra en la figura de abajo.
Se usa el símbolo que se muestra en la figura de la izquierda como el símbolo de la contenencia. Si queremos representar la no contenencia de conjuntos usaremos el mismo símbolo atravesado por una línea como se muestra en la figura de la derecha.
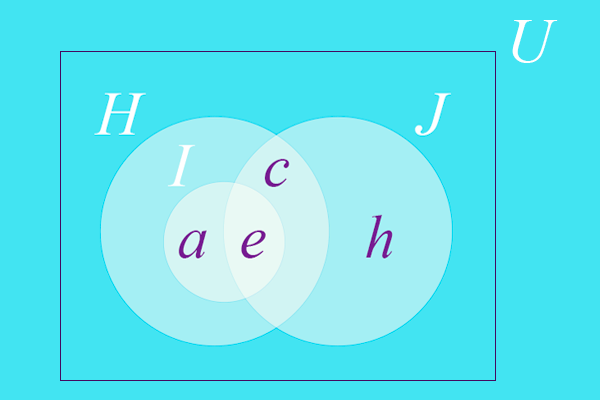
Definamos los conjuntos `H={a,c,e}`, `I={a,e}` y `J={c,e,h}`. ¿Crees que existe alguna relación de contenencia entre estos conjuntos?
Fíjate bien, recuerda que un conjunto está contenido en otro si cada uno de sus elementos pertenece también al otro conjunto. En este caso cada elemento del conjunto `I` pertenece también al conjunto `H`, decimos entonces que `I` está contenido en `H`, o que `I` es subconjunto de `H`.
¿Crees que el conjunto `J` está contenido en el conjunto `H`? Si observas con atención, notarás que hay un elemento de `J` que no está en `H`. Es decir, no se cumple la condición que cada elemento de `J` esté también en `H`. Se puede asegurar entonces que `J` no está contenido en `H`, o lo que es igual, que `J` no es subconjunto de `H`.
