
/es/los-decimales/fraccion-a-decimal-con-resultado-periodico/content/
Todo decimal exacto puede ser expresado también como fracción. Aprende cómo hacerlo aquí.
Observa el siguiente ejemplo: tomemos el decimal veinticinco centésimas: . Veinticinco centésimas es el resultado de dividir la unidad en cien partes iguales (centésimas) y tomar veinticinco de estas:

Recuerda que la expresión también puede ser interpretada como unidades de en total. Así, tomar partes de puede ser representado como veinticinco de cien: . Por lo tanto esta fracción representa exactamente lo mismo que , ahora solo hay que simplificarla:
Si se hace esto, se llegará exactamente al lugar de la recta en el que se ubica Por lo tanto, :
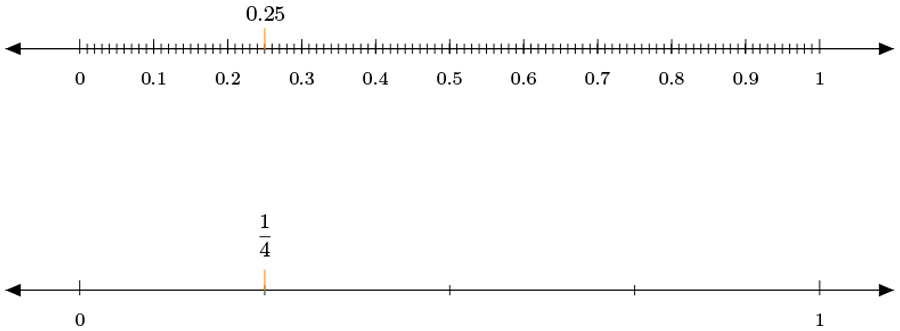
Si realizas la división , para convertir un cuarto a decimal, podrás comprobar este resultado.
Una forma resumida de realizar este procedimiento es la siguiente: dado un número decimal exacto, se corre la coma hacia la derecha tantas veces como sea necesario hasta que el último número tome el lugar de las unidades, después se divide la cantidad resultante entre un uno seguido de tantos ceros como fue corrida la coma.
En el caso de es necesario correr la coma hacia la derecha dos veces: si se traslada una vez, se obtiene , al trasladarla una segunda vez se llega al número . Luego de esto se divide en un uno seguido por dos ceros: . De esta forma se llega rápidamente a la fracción .
Observa otro ejemplo, encontremos una fracción equivalente al decimal exacto .
En esta ocasión es necesario correr la coma cuatro veces. Así, se transforma en .
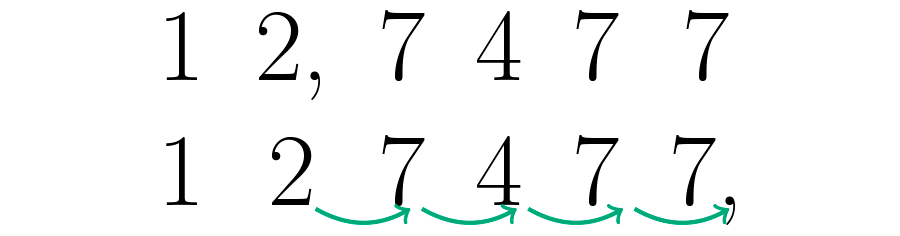
Después divide el número resultante, , entre un uno seguido de tantos ceros como veces se trasladó la coma en el paso anterior. Es decir, se debe dividir en .
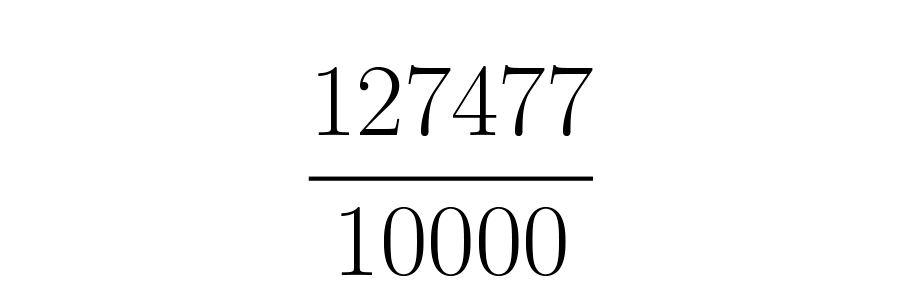
Si es posible simplificar, se hace; si no, se deja la fracción tal y como está. Como esta vez la fracción es irreducible, se tiene que .
/es/los-decimales/decimales-periodicos-puros-a-fraccion/content/