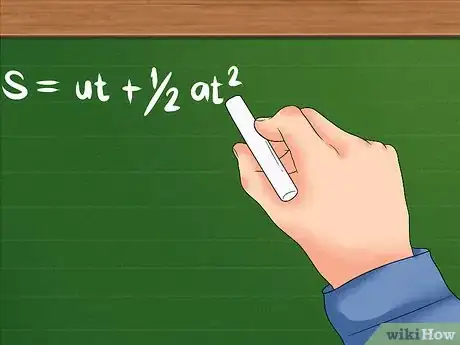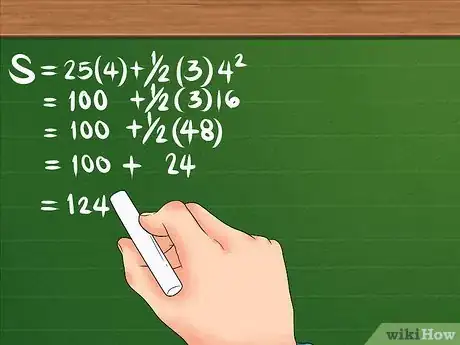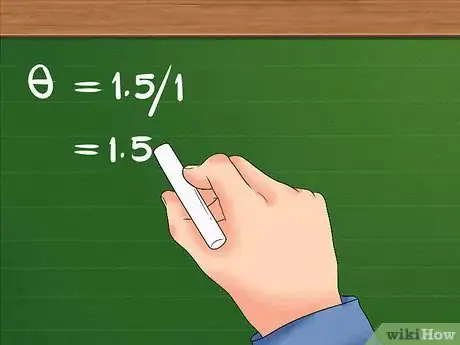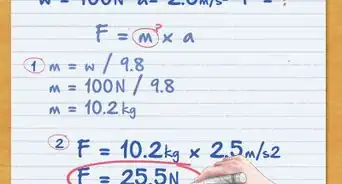How to Calculate Displacement

Last Updated: January 25, 2023 References

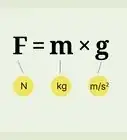
Displacement in physics refers to on object's change in position. When you calculate displacement, you measure how "out of place" on object is based on its initial location and its final location. The formula you use for calculating displacement will depend on variables that are provided to you in a given problem. Follow these steps to calculate displacement.

Part 1

Part 1 of 5:

Calculating Resultant Displacement

1
Use the resultant displacement formula when units of distance are used to specify your initial and final location. Though distance is different than displacement, resultant displacement problems will specify how many "feet" or how many "meters" an object has traveled. You will use these units of measurement to calculate displacement, or how far out of position the object is based on its original point.^{[1]
X
Research source}
- The resultant displacement formula is written as: S = √x²+y². "S" stands for displacement. X is the first direction that the object is traveling and Y is the second direction that the object is traveling. If your object only travels in one direction, then Y = 0.
- An object can only travel in two directions maximum, since moving along the north/south or east/west axes will be considered neutral movement.
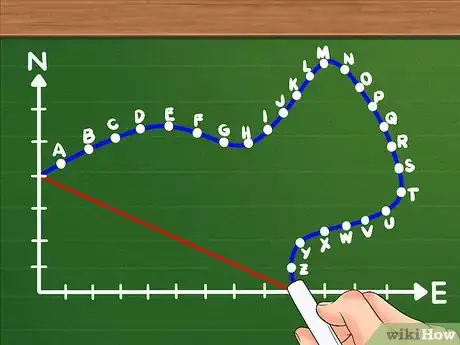
2
Connect the points based on order of movement and label them from A-Z. Use a ruler to make straight lines from point to point.^{[2]
X
Research source}
- Also remember to connect your starting point to your end point using a straight line. This is the displacement we will be calculating.
- For example, if an object travels east 300 feet and north 400 feet, it will form a right triangle. AB will form the first leg of the triangle and BC will form the second leg. AC will form the hypotenuse of the triangle, and its value will be the amount of the object's displacement. In this example, the two directions are "east" and "north."
Advertisement
3
Input the direction values for x² and y². Now that you know the two directions your object is traveling in, input the values into their respective variables.^{[3]
X
Research source}
- For example, x = 300 and y = 400. Your formula should look like this: S = √300² + 400².
4
Compute the formula using the order of operations. Square 300 and 400 first, then add them, and then find the square root of that sum.^{[4]
X
Research source}
- For example: S = √90000 + 160000. S = √250000. S = 500. You now know that displacement is equal to 500 feet.

Part 2

Part 2 of 5:

When Velocity and Time Values are Specified

1
Use this formula when the problem specifies the object's velocity and time taken. Some math problems will not specify values of distance, but will tell you how long an object was moving and how fast it was moving. You can calculate displacement using these time and speed values.
- In this case, the formula would be: S = 1/2(u + v)t. U = the object's initial velocity, or how fast it started going in a certain direction. V = the object's final velocity, or how fast it was going at its last location. T = the time the object took to get there.^{[5]
  X
  Research source}
- For example: A car is traveling down the road for 45 seconds (time taken). The car turned west at 20 m/s (initial velocity) and by the end of the street, it was traveling at 23 m/s (final velocity).Calculate the displacement based on these factors.
2
Input the values for velocity and time into their respective variables. Now that you know how long the car drove for, how fast it moved in the beginning, and how fast it was moving in the end, you can find the distance from the initial location to the final location.^{[6]
X
Research source}
- Your formula will look like this: S = 1/2(20 + 23)45.
3
Calculate the formula once you have input the values into their correct places. Remember to follow the order of operations, otherwise displacement will turn out to be a completely different value.^{[7]
X
Research source}
- For this formula, it's okay if you accidentally switch initial and final velocity. Since you will be adding these numbers first, it doesn't matter where they are in the parentheses. For other formulas, however, switching initial with final velocity will give you a different displacement value.
- Your formula will look like this: S = 1/2(43)45. First divide 43 by 2, which will give you 21.5 Then multiply 21.5 by 45, which should give you 967.5 meters. 967.5 is your displacement value, or how far your car is from its original spot.

Part 3

Part 3 of 5:

When Initial Velocity, Acceleration, and Time Values are Specified

1
Employ a modified formula when acceleration is specified along with initial velocity and time. Some problems will only tell you how fast an object was moving in the beginning, how fast it began to accelerate, and how long the object traveled for. You will need the following formula.
- The formula for this problem is as follows: S = ut + 1/2at². "U" still represents initial velocity; "A" is the object's acceleration, or how fast its velocity begins to change. "T" can either mean the total time taken, or it can be a certain amount of time an object accelerated for. Either way, it will be identified by units of time such as seconds, hours, etc.^{[8]
  X
  Research source}
- Say a car traveling at 25 m/s (initial velocity) begins accelerating at 3 m/s2 (acceleration) for 4 seconds (time). What is the displacement of the car after 4 seconds?^{[9]
  X
  Research source}
2
Plug in the values where they belong in the formula. Unlike the previous formula, only initial velocity is represented here, so be sure you input the correct data.^{[10]
X
Research source}
- Based on the example data above, your formula should look like this: S = 25(4) + 1/2(3)4². It will help if you add parentheses around your acceleration and time values to help you keep the numbers separate.
3
Calculate displacement by performing the necessary order of operations. A quick way to help you remember the order of operations is the mnemonic "Please excuse my dear Aunt Sally." This represents the correct order of parentheses, exponents, multiplication, division, addition, and subtraction.^{[11]
X
Research source}
- Let's revisit the formula: S = 25(4) + 1/2(3)4². First, square 4, which gives you 16. Then multiply 16 by 3, which gives you 48; also multiply 25 by 4, giving you 100. Divide 48 by 2, which is 24. Your equation should now look like this: S = 100 + 24. Once you add the two values together, displacement will equal 124 meters.^{[12]
  X
  Research source}

Part 4

Part 4 of 5:

Calculating Angular Displacement

1
Find angular displacement when an object travels in a curved path. Though you will still be calculating displacement using a straight line, you will need to find the difference between an object's initial and final location when it moves in an arc.
- Think of a girl sitting on a merry-go-round. As she spins along the outside of the ride, she will travel in a curved path. Angular displacement seeks to measure the shortest distance between the initial location and final location when an object isn't moving in a straight line.
- The formula for angular displacement is: θ = S/r, where "S" stands for linear displacement, "r" stands for radius, and "θ" represents angular displacement. Linear displacement is how far an object travels along an arc. Radius is the distance an object is from the center of a circle. Angular displacement is the value we are looking for.^{[13]
  X
  Research source}
2
Input the linear displacement and radius values into the equation. Remember that radius is the distance from the center of a circle; some problems may give you the circle's diameter, in which case you will need to divide it by 2 to find the radius.
- Here is a sample problem: A girl rides a merry-go-round. Her seat is at a distance of 1 meter from the center (radius). If the girl moves along an arc length of 1.5 meters (linear displacement), what is her angular displacement?
- Your equation should look like this: θ = 1.5/1.
3
Divide linear displacement by the radius. This will give you the angular displacement of the object.^{[14]
X
Research source}
- After dividing 1.5 by 1, you are left with 1.5. The angular displacement of the girl is 1.5 radians.
- Since angular displacement calculates how much an object has rotated from its original position, it will need to be measured as an angle, not a distance. Radians are units used to measure angles.

Part 5

Part 5 of 5:

Understanding Displacement

1
Know that "distance" means something different than "displacement." Distance refers to how far an object has traveled in total.
- Distance is what is known as a "scalar quantity." It refers to how much ground an object has covered without considering the direction the object is traveling.^{[15]
  X
  Research source}
- For example, if you walk 2 feet east, 2 feet south, 2 feet west, and then 2 feet north, you will be back in your original position. Though you will have traveled a total distance of 10 feet, you will have been displaced 0 feet because your final location is the same as your original location (your path resembles that of a box).^{[16]
  X
  Research source}
2
Understand that displacement is the difference between two locations. Displacement is not a total sum of motion like distance; it focuses on the area between your initial location and final location.^{[17]
X
Research source}
- Displacement is called a "vector quantity" and refers to an object's change in position with regards to the direction an object is moving.
- Say you head east for 5 feet. If you go back west 5 feet, you will be traveling in the opposite direction of your original location. Even though you will have walked 10 feet total, you won't have changed your position; your displacement then is 0 feet.
3
Remember the words "back and forth" when trying to imagine displacement. Going in the opposite direction cancels out the displacement of an object.
- Picture a football coach pacing back and forth along the sidelines.^{[18]
  X
  Research source} As he yells things at his players, he will have moved from left to right multiple times. If you watch him the entire time he is moving from left to right, you are observing the total distance he is traveling. But, say the coach stops to talk to the quarterback on the sidelines. If he is in a spot that is different than before he started pacing, you are looking at the coach's displacement.^{[19]
  X
  Research source}
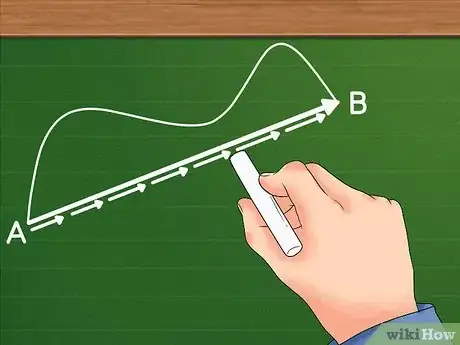
4
Know that displacement is measured using a straight line, not a curved path.^{[20]
X
Research source} To find displacement, you will need to find the shortest, most efficient way of measuring the difference between two points.
- A curved path will lead you from your initial location to your final location, but it is not the shortest path. To help you visualize this, imagine you are walking in a straight line and encounter a pillar. You can't walk through this pillar, so you walk around it. Though you will end up in the same position as if you walked through the pillar, you will have needed to take extra steps to get to your destination.
- Though displacement prefers a straight line, know that you can measure the displacement of an object that is traveling in a curved path. This is called "angular displacement," and it can be calculated by finding the straightest path that leads from initial location to final location.
5
Understand that displacement can be a negative value, unlike distance. If your final location is arrived at by moving in a direction opposite than when you started, you will be displaced negatively.^{[21]
X
Research source}
- For example, say you walked 5 feet east and then 3 feet west. Though technically you are still 2 feet from your original location, your displacement would be -2 because you are moving in the opposite direction. Your distance will always be a positive value because you can't "un-travel" amount of feet, miles, etc.
- Negative displacement does not mean that the displacement is getting decreased. It simply means that the displacement is taking an opposite direction.
6
Realize that sometimes distance and displacement values can be the same. If you walk straight for 25 feet and stop, the amount of ground covered will be the same as how far you are from your original location.
- This only applies to when you travel to one location from your initial location in a straight line. For example, say you live in San Francisco, California and land a new job in Las Vegas, Nevada. You need to move out to Las Vegas in order to be closer to your job. If you take a plane that flies straight from San Francisco to Las Vegas, you will have traveled 417 miles (671 km) and will be displaced 417 miles (671 km).
- If you take a car from San Francisco to Las Vegas, however, you will be displaced 417 miles (671 km) but will have traveled 563 miles (906 km).^{[22]
  X
  Research source} Since driving usually involves changing directions (east on this highway, west on that highway), you will have traveled farther than the shortest distance between the two cities.

Community Q&A

Question

A car accelerates from 8m/s to 16m/s in 10m/s. What is the displacement?

Community Answer

You'll need to know the distance first. After you find it, use the equation Displacement = 1/2(initial velocity+ final velocity) • time.
Question

How can I calculate displacement of circular objects?

Community Answer

Displacement refers to an objects change in position so in case an object moves a complete circle (360 degrees) it will not have any displacement for a non complete circle it is easy to find the distance by using the below formula. Chord length = 2√(r^2 - d^2) where, r = radius of the circle d = perpendicular distance from the chord to the circle center. Chord of a circle is a line segment whose ends lie on the circle.
Question

How do I calculate the resultant displacement if a man travels 1.5m towards east, then 2.0m south and finally 4.5m towards east?

Community Answer

What I would do is start by graphing your vectors, adding tip to tail, which will leave you with an end point. Assuming we started at (0,0) it would be (6, -2) in your case. Then you use the distance formula, √(x1-x2)^2 + (y1-y2)^2. So then you have √(0-6)^2 + (0-(-2))^2, which, when simplified, is the √40, or 6.324555.