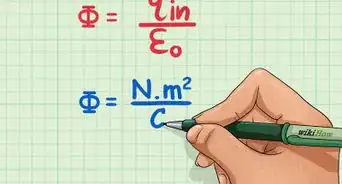How to Convert Maxwell's Equations into Differential Form

Last Updated: May 18, 2017 Approved

In electrodynamics, Maxwell's equations, along with the Lorentz Force law, describe the nature of electric fields $\mathbf {E}$ and magnetic fields $\mathbf {B} .$ These equations can be written in differential form or integral form. Even though the two forms are completely equivalent, most students first learn the integral form because it is more applicable to volumes and fluxes, and thus more useful for calculations.

Part 1

Part 1 of 4:

Gauss' Law

1
Begin with Gauss' law in integral form.
- $\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {Q}{\epsilon _{0}}}$
2
Rewrite the right side in terms of a volume integral.
- $\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S} =\int _{V}{\frac {\rho }{\epsilon _{0}}}\mathrm {d} V$
Advertisement
3
Recall the divergence theorem. The divergence theorem says that the flux penetrating a closed surface $S$ $S$ that bounds a volume $V$ $V$ is equal to the divergence of the field $\mathbf {F}$ ${\mathbf {F}}$ inside the volume.
- $\oint _{S}\mathbf {F} \cdot \mathrm {d} \mathbf {S} =\int _{V}(\nabla \cdot \mathbf {F} )\mathrm {d} V$
4
Use the divergence theorem to rewrite the left side as a volume integral.
- $\int _{V}(\nabla \cdot \mathbf {E} )\mathrm {d} V=\int _{V}{\frac {\rho }{\epsilon _{0}}}\mathrm {d} V$
5
Set the equation to 0.
- ${\begin{aligned}\int _{V}(\nabla \cdot \mathbf {E} )\mathrm {d} V-\int _{V}{\frac {\rho }{\epsilon _{0}}}\mathrm {d} V&=0\\\int _{V}\left(\nabla \cdot \mathbf {E} -{\frac {\rho }{\epsilon _{0}}}\right)\mathrm {d} V&=0\end{aligned}}$
6
Convert the equation to differential form.
- The above equation says that the integral of a quantity is 0. Because the only quantity for which the integral is 0, is 0 itself, the expression in the integrand can be set to 0.
  - $\nabla \cdot \mathbf {E} -{\frac {\rho }{\epsilon _{0}}}=0$
- This leads to Gauss' law in differential form.
  - $\nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}$

Part 2

Part 2 of 4:

Gauss' Law for Magnetism

1
Begin with Gauss' law for magnetism in integral form.
- $\oint _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$
2
Invoke the divergence theorem.
- $\int _{V}(\nabla \cdot \mathbf {B} )\mathrm {d} V=0$
3
Write the equation in differential form.
- As with Gauss' Law, the same argument used above yields our answer.
  - $\nabla \cdot \mathbf {B} =0$

Part 3

Part 3 of 4:

Faraday's Law

1
Begin with Faraday's law in integral form.
- $\oint _{C}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S}$
2
Recall Stokes' theorem. Stokes' theorem says that the circulation of a field $\mathbf {F}$ ${\mathbf {F}}$ around the loop $C$ $C$ that bounds a surface $S$ $S$ is equal to the flux of $\operatorname {curl} \mathbf {F}$ $\operatorname {curl}{\mathbf {F}}$ over $S.$ $S.$
- $\oint _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {l} =\int _{S}(\nabla \times \mathbf {F} )\cdot \mathrm {d} \mathbf {S}$
3
Use Stokes' theorem to rewrite the left side as a surface integral.
- $\int _{S}(\nabla \times \mathbf {E} )\cdot \mathrm {d} \mathbf {S} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S}$
4
Set the equation to 0.
- ${\begin{aligned}\int _{S}(\nabla \times \mathbf {E} )\cdot \mathrm {d} \mathbf {S} +{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} &=0\\\int _{S}\left(\nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} &=0\end{aligned}}$
5
Convert the equation to differential form.
- ${\begin{aligned}\nabla &\times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}=0\\\nabla &\times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\end{aligned}}$

Part 4

Part 4 of 4:

The Ampere-Maxwell Law

1
Begin with the Ampere-Maxwell law in integral form.
- $\oint _{C}\mathbf {B} \cdot \mathrm {d} \mathbf {l} =\mu _{0}\int _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} +\mu _{0}\epsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S}$
2
Invoke Stokes' theorem.
- $\int _{S}(\nabla \times \mathbf {B} )\cdot \mathrm {d} \mathbf {S} =\mu _{0}\int _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} +\mu _{0}\epsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S}$
3
Set the equation to 0.
- ${\begin{aligned}\int _{S}(\nabla \times \mathbf {B} )\cdot \mathrm {d} \mathbf {S} -\mu _{0}\int _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} -\mu _{0}\epsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {S} &=0\\\int _{S}\left(\nabla \times \mathbf {B} -\mu _{0}\mathbf {J} -\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {S} &=0\end{aligned}}$
4
Convert the equation to differential form.
- ${\begin{aligned}\nabla &\times \mathbf {B} -\mu _{0}\mathbf {J} -\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}=0\\\nabla &\times \mathbf {B} =\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\end{aligned}}$