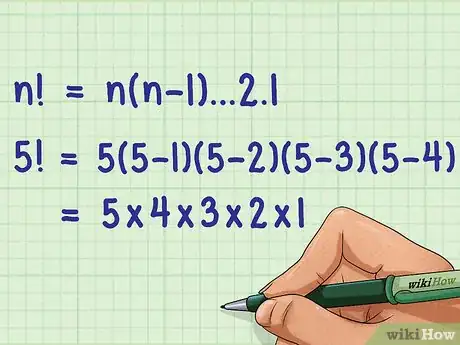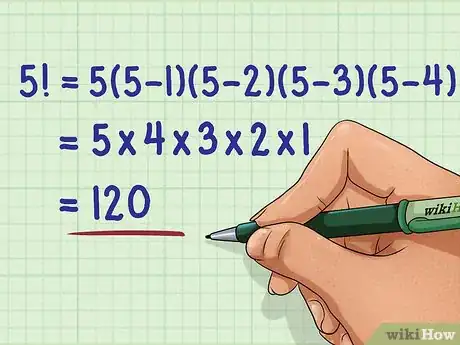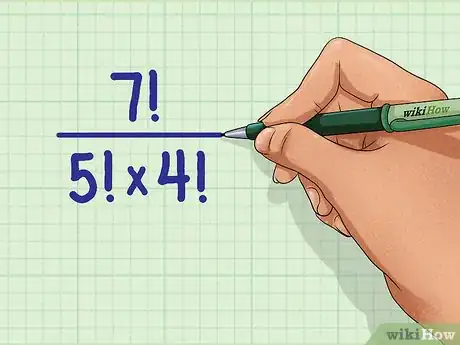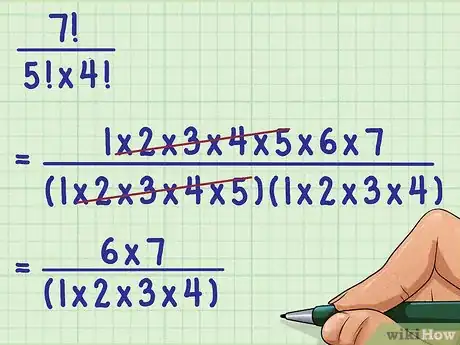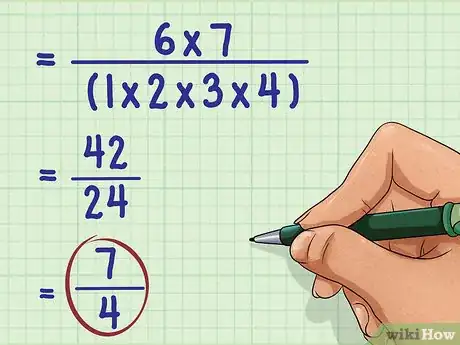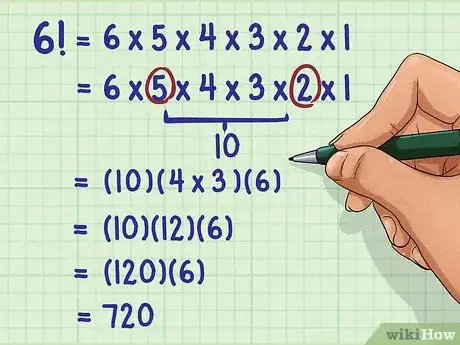This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 7 references cited in this article, which can be found at the bottom of the page.
wikiHow marks an article as reader-approved once it receives enough positive feedback. In this case, 85% of readers who voted found the article helpful, earning it our reader-approved status.
This article has been viewed 157,167 times.
Learn more...
Factorials are commonly used when calculating probability and permutations, or possible orders of events.[1] A factorial is denoted by a sign, and it means to multiply together all the numbers descending from the factorial number. Once you understand what a factorial is, it is simple to compute, especially with the aid of a scientific calculator.
Steps
Computing a Factorial
-
1Determine the number you are computing the factorial for. A factorial is denoted by a positive integer and an exclamation point.[2]
- For example, if you need to compute the factorial for 5, you will see .
-
2Write out the sequence of numbers to be multiplied. A factorial is simply multiplying the natural numbers that descend sequentially from the factorial number, down to 1.[3] Speaking formulaically, , where equals any positive integer.[4]
- For example, if you are computing , you would compute or, denoted more simply: .
Advertisement -
3Multiply the numbers together. You can compute a factorial quickly using a scientific calculator, which should have a sign. If you are computing by hand, to make it easier, first look for pairs of factors that multiply to equal 10.[5] Of course, you can also ignore the 1, since any number multiplied by 1 equals that number.
- For example, if computing , disregard the 1, and first calculate . Now all you are left with is . Since , you know that .
Simplifying a Factorial
-
1Determine the expression you are simplifying. Often this will be stated as a fraction.[6]
- For example, you might need to simplify .
-
2Write out the factors of each factorial. Since the factorial is a factor of any factorial larger than it, to simplify, you need to look for factors that you can cancel out.[7] This is easy to do if you write out each term.
- For example, if simplifying , rewrite as
-
3Cancel out any terms common to the numerator and denominator.[8] This will simplify the numbers leftover that you need to multiply.
- For example, since is a factor of , you can cancel out from the numerator and denominator:
- For example, since is a factor of , you can cancel out from the numerator and denominator:
-
4Complete the calculations. Simplify if possible. This will give you the final, simplified expression.[9]
- For example:
So, simplified is .
- For example:
Doing Sample Factorial Problems
-
1Evaluate the expression 8!.
- If using a scientific calculator, hit the key, followed by the key.
- If solving by hand, write out the factors to be multiplied:
- Disregard the 1:
- Pull out :
- Group any other easily multiplied numbers first, then multiply all the products together:
So, .
-
2Simplify the expression: .
- Write out the factors of each factorial:
- Cancel out terms common to the numerator and denominator:
- Complete the calculations:
So, the expression simplifies to .
- Write out the factors of each factorial:
-
3Try the following problem. You have 6 paintings you would like to display in a row on your wall. How many different ways can you order the paintings?
- Since you are looking for different ways you can order objects, you can simply solve by finding the factorial for the number of objects.
- The number of possible arrangements for 6 paintings hung in a row can be solved by finding .
- If using a scientific calculator, hit the key, followed by the key.
- If solving by hand, write out the factors to be multiplied:
- Disregard the 1:
- Pull out :
- Group any other easily multiplied numbers first, then multiply all the products together:
So, 6 paintings hung in a row can be ordered 720 different ways.
-
4Try the following problem. You have 6 paintings. You would like to display 3 of them in a row on your wall. How many different ways can you order 3 of the paintings?
- Since you have 6 different paintings, but you are only choosing 3 of them, you only need to multiply the first 3 numbers in the sequence for the factorial of 6. You can also use the formula , where equals the number of objects you are choosing from, and equals the number of objects you are using. This formula only works if you have no repetitions (an object can’t be chosen more than once), and order does matter (that is, you want to find how many different ways things can be ordered).[10]
- The number of possible arrangements for 3 paintings chosen from 6 and hung in a row can be solved by finding .
- Subtract the numbers in the denominator:
- Write the factors of each factorial:
- Cancel out terms common to the numerator and denominator:
- Complete the calculations:
So, 3 paintings chosen from 6 can be ordered in 120 different ways if hung in a row.
Community Q&A
-
QuestionIs there a short cut?
 DonaganTop AnswererThe factorial notation is the short cut. For example, you can write 8! instead of writing 8x7x6x5x4x3x2x1 = 40,320.
DonaganTop AnswererThe factorial notation is the short cut. For example, you can write 8! instead of writing 8x7x6x5x4x3x2x1 = 40,320. -
QuestionHow do I calculate factorials of floating point numbers like 0.5?
 DonaganTop AnswererA factorial is defined as involving integers only.
DonaganTop AnswererA factorial is defined as involving integers only. -
QuestionWhy and where is the 0! = 1 used?
 TechnistCommunity AnswerA simple problem with straightforward factorials would be: "How many ranges can you arrange n objects?" Here n is 0, and technically, there's only 1 way of arranging it. As for where, you might sometimes get problems related with combinatorics or the binomial theorem such as 12C12 or 4C0, which expand to 12! / (0!12!) and 4! / (0!4!), respectively. That's where 0! will appear.
TechnistCommunity AnswerA simple problem with straightforward factorials would be: "How many ranges can you arrange n objects?" Here n is 0, and technically, there's only 1 way of arranging it. As for where, you might sometimes get problems related with combinatorics or the binomial theorem such as 12C12 or 4C0, which expand to 12! / (0!12!) and 4! / (0!4!), respectively. That's where 0! will appear.
References
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html
- ↑ https://www.calculatorsoup.com/calculators/discretemathematics/factorials.php
- ↑ https://www.mathsisfun.com/numbers/factorial.html
- ↑ http://mathworld.wolfram.com/Factorial.html
- ↑ http://www.themathpage.com/aprecalc/factorial.htm
- ↑ https://www.chilimath.com/lessons/intermediate-algebra/simplifying-factorials-with-variables/
- ↑ http://www.themathpage.com/aprecalc/factorial.htm
- ↑ http://www.purplemath.com/modules/factorial.htm
- ↑ https://www.chilimath.com/lessons/intermediate-algebra/simplifying-factorials-with-variables/
About This Article
To do factorials, start by determining which number you're computing the factorial for, which will be the number that's in front of the exclamation point. Then, write out all of the numbers that descend sequentially from that number until you get to 1. Finally, multiply all of the numbers together. For example, if you're trying to compute the factorial of 5, you would write "5, 4, 3, 2, 1." Then, you would multiply 5 by 4 to get 20, 20 by 3 to get 60, 60 by 2 to get 120, and 120 by 1 to get 120. Therefore, your answer would be 120. To learn how to simplify factorials and solve equations with factorials in them, scroll down!