How to Find the Five Number Summary in Statistics

The five number summary is an important way of organizing data to show statistical importance through dispersion. This summary consists of the minimum, Quartile 1 (Q1), median (Q2), Quartile 3 (Q3), and the maximum; usually organized in that specific order on a box plot. The lower quartile (Q1) consists of the lower 25% of the data while the upper quartile (Q3) contains 25% of the highest numbers in the data set or 75% of the entire data. This statistical analysis is very useful for larger data because the median identifies the center of the data, the minimum and maximum gives the length of the data and the quartiles allows for further analysis of an assortment. [1]

Part 1
Part 1 of 6:

Preparing the Data for Calculation

  1. Image titled Amount numbers 1.png
    1
    Determine the amount of numbers in your data set. You can do this by counting all of the numbers in the data set.
    • Example: In a data set 1,3,4,5,11,12,14,20,11,2 there are 10 numbers in the data set
  2. Image titled Organize 1.png
    2
    Organize the data in increasing order. Starting with the smallest number value up to the largest number.
    • Organize the data by scanning and writing down the numbers in increasing number.
    • While scanning cross out the numbers that were already used to keep track
    • Example: In a data set 1,3,4,5,11,12,14,20,11,2 the numbers would be organized as 1,2,3,4,5,11,11,12,14,20
    Advertisement
  3. Image titled Equations2 1.png
    3
    Write down or memorize the equations for both quartiles and the median.[2]
    • The 1st Quartie equation ¼ (n+1)
    • The median equation ½(n+1)
    • The 3rd Quartile ¾(n+1)
    4. Advertisement
Part 2
Part 2 of 6:

Finding the Minimum and Maximum

Image titled Min max 1.png
  1. 1
    Find the smallest and the largest numbers of the total data set. In a data set organized in increasing order the minimum is the first number and the maximum in the last number.
    • Example: In a data set 1,2,3,4,5,11,11,12,12,14,20 (organized in increasing order) the minimum is 1 (lowest) and maximum is 20 (largest).
Part 3
Part 3 of 6:

Calculating the First Quartile

  1. Image titled !st Quartile n 1.png
    1
    Plug in the value of n in the First Quartile formula. ¼(n+1)
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, the equation will be ¼(10+1)
  2. Image titled 1st quart solve 1.png
    2
    Solve the equation: Solving the equation will not give the exact answer of Quartile 1, it will instead give the position of the number.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, the equation will be ¼(10+1) which equals 11/4 or 2.75. This means that the first Quartile is located at position 2.75 in the data set.
  3. Image titled 1st quat between 1.png
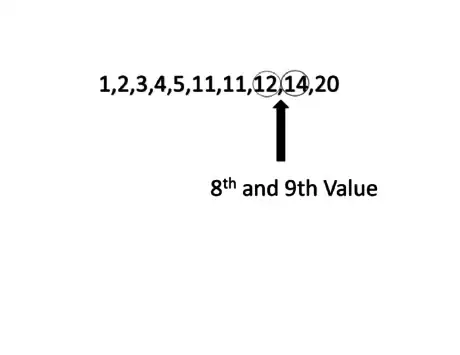
    3
    Use the solution from the equation to find the number at that position. After solving the equation, use the answer to find the location in the data set where the quartile is located.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 because the equation gave the decimal 2.75, the 1st Quartile is located between the 2nd and 3rd numbers in the data set
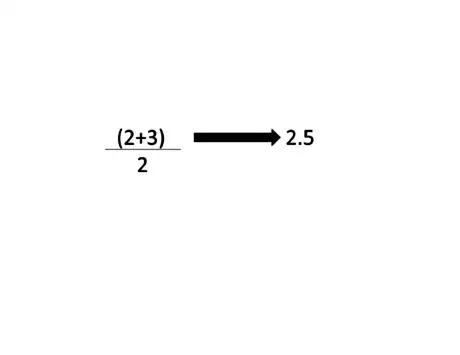
  4. 4
    Find the average of the numbers to the left and to the right of the position.If a decimal is calculated
    5. Advertisement
Part 4
Part 4 of 6:

Find the Median

  1. Image titled Median n 1.png
    1
    Plug in the value of n into the Median formula. ½(n+1)
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, The equation will be ½(10+1)
  2. Image titled Median Solution 1.png
    2
    Solve the equation. Solving the equation will give you the location of the number (median) in the data set.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, The equation ½(10+1) will equal 5.5, which places the median at position 5.5
  3. 3
    Locate the median in the data set. Use the position received from solving the median equation to locate the data.
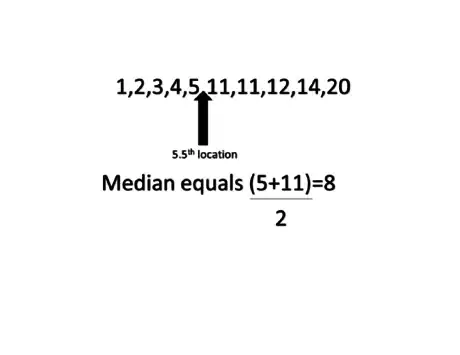
  4. Image titled Median even 1.png
    4
    Find the average of the numbers right and left of the value received from the equation if it is an even number of data.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10 the median is located position 5.5 which is between the 5th and 6th number. To find the median we will take the average of the 5th and 6th numbers. Taking the average means adding the two numbers together and dividing by 2.
    • Example: 1,2,3,4,5,11,11,12,14,20 the numbers beside 5.5 is 5 and 11 therefore the equation goes (5+11)/2=8. The Median then equals 8.
  5. Image titled Median odd 1.png
    5
    If it is an odd number of data then the position given by the equation will be the exact position of the median.
    • Example:#*Example: In a data set 1,2,3,4,5,11,11,12,14,20,20 n=11, plug 11 in equation ½(11+1) the median will be at position 6 so the median is 11.
    6. Advertisement
Part 5
Part 5 of 6:

Calculate the Upper Quartile

  1. Image titled 3rd Quarte nn 1.png
    1
    Plug in the value of n in the Third Quartile formula. ¾ (n+1)
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, The equation will be ¾ (10+1)
  2. Image titled 3rd Quarte solve 1.png
    2
    Solve the equation. The solving of the equation will not give the 3rd Quartile it will instead give the position of the number.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 n=10, The equation will be ¾ (10+1) will equal 33/4 .This means that the third Quartile is located at position 8.25.
  3. Image titled 3rd Quarte between 1.png
    3
    Use the solution from the equation to find the number at the position. After computing the equation use the answer to find the location in the data set where the quartile is located.
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 the number is in the 8.25th position, therefore, the 3rd Quartile is between the 8th and 10th numbers
  4. Image titled 3rd Quarte solution 1.png
    4
    Find the average of the numbers to the left and the right of the position if a decimal is calculated from the equation.
    • Add the left and right numbers together then divide by two.
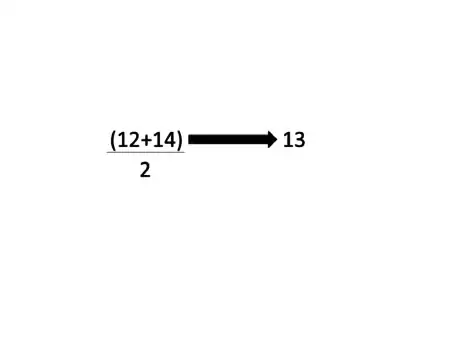
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 the number is in the 8.25th position which is between the 8th and 10th numbers meaning we take (12+14) then divide by 2 which equals 13
    5. Advertisement
Part 6
Part 6 of 6:

Completing the 5 Number Summary

  1. Image titled 5 numbaa 1.png
    1
    Write down the 5 number summary using commas to separate them. Use the order minimum, 1st Quartile, Median, 3rd Quartile, Maximum.
    • Doing this will help differentiate each part of the data
    • Example: In a data set 1,2,3,4,5,11,11,12,14,20 the 5 number summary will be 1,2.5,8,13,20

You Might Also Like

Convert from Binary to Decimal
How to
Convert from Binary to Decimal
Convert from Decimal to Binary
How to
Convert from Decimal to Binary
Convert Milliliters (mL) to Grams (g)
How to
Convert Milliliters (mL) to Grams (g)
Calculate Volume in Litres
How to
Calculate Volume in Litres
Convert Minutes to HoursConverting Minutes to Hours in Decimal or Hour & Minute Format
Convert Celsius (°C) to Fahrenheit (°F)°C to °F Conversion: A Complete Guide
Convert Grams to KilogramsConversion Factor for Grams to Kilograms (and Kilograms to Grams)
Convert a Number from Decimal to IEEE 754 Floating Point Representation
How to
Convert a Number from Decimal to IEEE 754 Floating Point Representation
Convert Kilometers to Miles
How to
Convert Kilometers to Miles
Convert Feet to Meters
How to
Convert Feet to Meters
Calculate Cubic Inches
How to
Calculate Cubic Inches
Convert Hexadecimal to Binary or Decimal
How to
Convert Hexadecimal to Binary or Decimal
Convert Seconds to MinutesTurn Seconds Into Minutes: Breakdown, Practice Problems, & More
Convert Binary to Hexadecimal
How to
Convert Binary to Hexadecimal
Advertisement

References

  1. ↑ https://www150.statcan.gc.ca/n1/edu/power-pouvoir/ch12/5214877-eng.htm
  2. ↑ https://www.statisticshowto.datasciencecentral.com/how-to-find-a-five-number-summary-in-statistics/
  3. ↑ https://www.purplemath.com/modules/boxwhisk2.htm

About This Article

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time. This article has been viewed 34,263 times.
9 votes - 69%
Co-authors: 4
Updated: September 16, 2022
Views: 34,263
Categories: Conversion Aids
Advertisement