wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 127 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 3,177,616 times.
Learn more...
Do you need to convert a set of binary numbers (0s and 1s) to a decimal value? There are several easy ways to convert binary numbers, but we'll focus on the easiest, most time-saving solutions! This wikiHow article will teach you how to do a binary to decimal conversion using positional notation, by doubling, and by using a simple Microsoft Excel binary to decimal calculator sheet.
Steps
Converter
How to Use Positional Notation
-
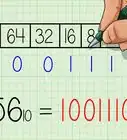
1Write down the binary number and list the powers of 2 from right to left. Let's say we want to convert the binary number 100110112 to decimal. First, write it down. Then, write down the powers of two from right to left. Start at 20, evaluating it as "1". Increment the exponent by one for each power. Stop when the amount of elements in the list is equal to the amount of digits in the binary number. The example number, 10011011, has eight digits, so the list, with eight elements, would look like this: 128, 64, 32, 16, 8, 4, 2, 1
-
2Write the digits of the binary number below their corresponding powers of two. Now, just write 10011011 below the numbers 128, 64, 32, 16, 8, 4, 2, and 1 so that each binary digit corresponds with its power of two. The "1" to the right of the binary number should correspond with the "1" on the right of the listed powers of two, and so on. You can also write the binary digits above the powers of two, if you prefer it that way. What's important is that they match up.Advertisement
-
3Connect the digits in the binary number with their corresponding powers of two. Draw lines, starting from the right, connecting each consecutive digit of the binary number to the power of two that is next in the list above it. Begin by drawing a line from the first digit of the binary number to the first power of two in the list above it. Then, draw a line from the second digit of the binary number to the second power of two in the list. Continue connecting each digit with its corresponding power of two. This will help you visually see the relationship between the two sets of numbers.
-
4Write down the final value of each power of two. Move through each digit of the binary number. If the digit is a 1, write its corresponding power of two below the line, under the digit. If the digit is a 0, write a 0 below the line, under the digit.
- Since "1" corresponds with "1", it becomes a "1." Since "2" corresponds with "1," it becomes a "2." Since "4" corresponds with "0," it becomes "0." Since "8" corresponds with "1", it becomes "8," and since "16" corresponds with "1" it becomes "16." "32" corresponds with "0" and becomes "0" and "64" corresponds with "0" and therefore becomes "0" while "128" corresponds with "1" and becomes 128.
-
5Add the final values. Now, add up the numbers written below the line. Here's what you do: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. This is the decimal equivalent of the binary number 10011011.
-
6Write the answer along with its base subscript. Now, all you have to do is write 15510, to show that you are working with a decimal answer, which must be operating in powers of 10. The more you get used to converting from binary to decimal, the more easy it will be for you to memorize the powers of two, and you'll be able to complete the task more quickly.
-
7Use this method to convert a binary number with a decimal point to decimal form. You can use this method even when you want to covert a binary number such as 1.12 to decimal. All you have to do is know that the number on the left side of the decimal is in the units position, like normal, while the number on the right side of the decimal is in the "halves" position, or 1 x (1/2).
- The "1" to the left of the decimal point is equal to 20, or 1. The 1 to the right of the decimal is equal to 2-1, or .5. Add up 1 and .5 and you get 1.5, which is 1.12 in decimal notation.
How to Use Doubling
-
1Write down the binary number. This method does not use powers. As such, it is simpler for converting large numbers in your head because you only need to keep track of a subtotal. The first thing you need to do is to write down the binary number you'll be converting using the doubling method. Let's say the number you're working with is 10110012. Write it down.
-
2Starting from the left, double your previous total and add the current digit. Since you're working with the binary number 10110012, your first digit all the way on the left is 1. Your previous total is 0 since you haven't started yet. You'll have to double the previous total, 0, and add 1, the current digit. 0 x 2 + 1 = 1, so your new current total is 1.
-
3Double your current total and add the next leftmost digit. Your current total is now 1 and the new current digit is 0. So, double 1 and add 0. 1 x 2 + 0 = 2. Your new current total is 2.
-
4Repeat the previous step. Just keep going. Next, double your current total, and add 1, your next digit. 2 x 2 + 1 = 5. Your current total is now 5.
-
5Repeat the previous step again. Next, double your current total, 5, and add the next digit, 1. 5 x 2 + 1 = 11. Your new total is 11.
-
6Repeat the previous step again. Double your current total, 11, and add the next digit, 0. 2 x 11 + 0 = 22.
-
7Repeat the previous step again. Now, double your current total, 22, and add 0, the next digit. 22 x 2 + 0 = 44.
-
8Continue doubling your current total and adding the next digit until you've run out of digits. Now, you're down to your last number and are almost done! All you have to do is take your current total, 44, and double it along with adding 1, the last digit. 2 x 44 + 1 = 89. You're all done! You've converted 100110112 to decimal notation to its decimal form, 89.
-
9Write the answer along with its base subscript. Write your final answer as 8910 to show that you're working with a decimal, which has a base of 10.
-
10Use this method to convert from any base to decimal. Doubling is used because the given number is of base 2. If the given number is of a different base, replace the 2 in the method with the base of the given number. For example, if the given number is in base 37, you would replace the "x 2" with "x 37". The final result will always be in decimal (base 10).
Community Q&A
-
QuestionHow do you convert a negative decimal to binary?
 wikiHow Staff EditorThis answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff EditorThis answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
Staff Answer wikiHow Staff EditorStaff AnswerFirst, ignore the decimal sign and keep dividing the number by 2 until the quotient is 0, always writing down the remainder to the right of each quotient. Write down the remainders from bottom to top of the list to make a sequence of 1s and 0s, and divide the list up into groups of 4, starting at the end. Add extra 0s to the front of the list if you have to. To convert the binary representation into a negative number, “flip” the sequence so that each 0 becomes a 1 and each 1 becomes a 0. Add 1 to the sequence to get your final answer. Remember that 1 + 1 = 10 in binary.
wikiHow Staff EditorStaff AnswerFirst, ignore the decimal sign and keep dividing the number by 2 until the quotient is 0, always writing down the remainder to the right of each quotient. Write down the remainders from bottom to top of the list to make a sequence of 1s and 0s, and divide the list up into groups of 4, starting at the end. Add extra 0s to the front of the list if you have to. To convert the binary representation into a negative number, “flip” the sequence so that each 0 becomes a 1 and each 1 becomes a 0. Add 1 to the sequence to get your final answer. Remember that 1 + 1 = 10 in binary. -
QuestionCan you convert from binary to hexadecimal?
 wikiHow Staff EditorThis answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff EditorThis answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
Staff Answer wikiHow Staff EditorStaff AnswerYes. Binary is base 2, while hexadecimal is base 16. Hexadecimal numbers can be represented as the numbers 0-9 and the letters A-F (for numbers greater than 10). You’ll need to take a binary line of 4 numbers and multiply the numbers by 1, 2, 4, and 8, respectively, going from right to left. Add the results together to get your answer.
wikiHow Staff EditorStaff AnswerYes. Binary is base 2, while hexadecimal is base 16. Hexadecimal numbers can be represented as the numbers 0-9 and the letters A-F (for numbers greater than 10). You’ll need to take a binary line of 4 numbers and multiply the numbers by 1, 2, 4, and 8, respectively, going from right to left. Add the results together to get your answer. -
QuestionWhat is 11100.1010 binary in decimal?
 Community Answer1x2^4 + 1x2^3 + 1x2^2 + 0x2^1 + 0x2^0 + 1x2^-1 + 0x2^-2 + 1x2^-3 + 0x2^-4 = 29.6250
Community Answer1x2^4 + 1x2^3 + 1x2^2 + 0x2^1 + 0x2^0 + 1x2^-1 + 0x2^-2 + 1x2^-3 + 0x2^-4 = 29.6250
Warnings
-
⧼thumbs_response⧽
References
About This Article
1. Write down the binary number.
2. List the powers of two from right to left.
3. Write the digits of the binary number below their corresponding powers.
4. Connect the digits in the binary number with their corresponding powers.
5. Write down the final value of each power of two.
6. Add the final values.
7. Write the answer along with its base subscript.






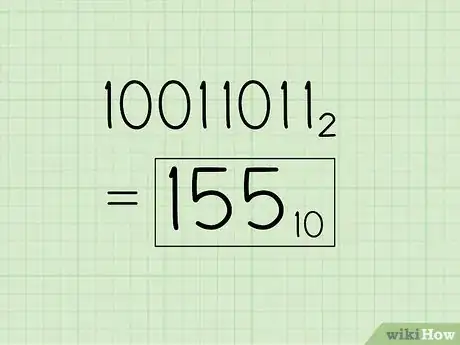
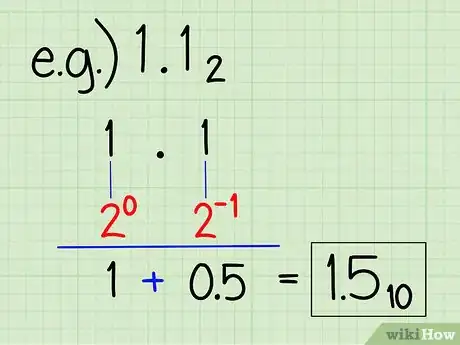









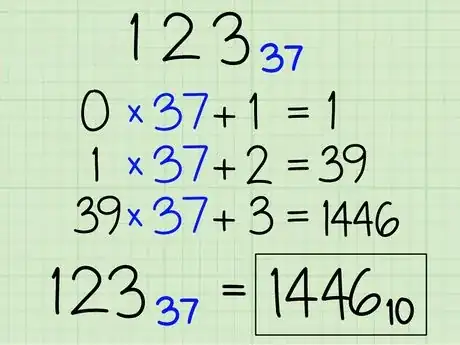




-to-Grams-(g)-Step-8-Version-5.webp)

-to-Fahrenheit-(°F)-Step-6-Version-2.webp)