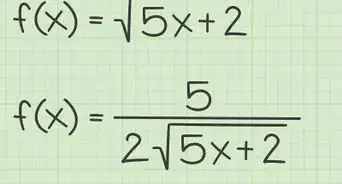X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time.
This article has been viewed 25,457 times.
Learn more...
In Fourier analysis, a Fourier series is a method of representing a function in terms of trigonometric functions. Fourier series are extremely prominent in signal analysis and in the study of partial differential equations, where they appear in solutions to Laplace's equation and the wave equation.
Preliminaries
- Let be a piecewise continuous function defined on Then the function may be written in terms of its Fourier series. We note that the sums begin with but because and we may write out the constant term separately and begin both sums with
- The coefficients and are known as Fourier coefficients. To decompose a function into its Fourier series, we must find these coefficients.
- To recognize what they are, we write out the function in terms of a basis In order for this basis to be useful, it must be orthonormal so that the Kronecker delta that equals if and otherwise. The expression below simply means that we are projecting onto
- For functions defined on the interval we define the following inner product. Notice that this inner product is normalized. The symbol denotes the complex conjugate.
- The functions and comprise the Fourier basis. With this in mind, we may write the Fourier coefficients below. When one substitutes with an element of the Fourier basis, the coefficient goes to unity. Hence the basis elements under this inner product form an orthonormal set.
- What is the interpretation of the constant term and why do we need an extra in the expression? This expression is in fact the average value of over the interval. (If the function is periodic, then it is the average value of the function over the entire domain.) The extra is there because of the boundaries and compensates for the fact that we are integrating over an interval with length
- To recognize what they are, we write out the function in terms of a basis In order for this basis to be useful, it must be orthonormal so that the Kronecker delta that equals if and otherwise. The expression below simply means that we are projecting onto
Steps
-
1Decompose the following function in terms of its Fourier series. Generally speaking, we may find the Fourier series of any (piecewise continuous - see the tips) function on a finite interval. If the function is periodic, then the behavior of the function in that interval allows us to find the Fourier series of the function on the entire domain.
-
2Identify the even and odd parts of the function. Every function may be decomposed into a linear combination of even and odd functions. The Fourier basis is convenient for us in that this series already separates these components. Therefore, by careful observation of which parts of the function are even and which are odd, we can do the integrals separately knowing which terms vanish and which do not.
- For our function, is even and is odd. This means that for and for
Advertisement -
3Evaluate the constant term. The constant term is actually the term of the cosines. Note that does not contribute to the integral because any constant function is even.
-
4Evaluate the Fourier coefficients. Here, we may evaluate by way of integration by parts. It is useful to recognize that and It is also worth noting that the integral of a trigonometric function over one period vanishes.
-
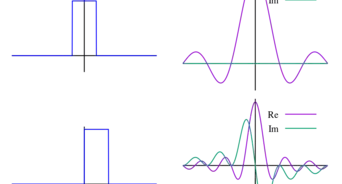
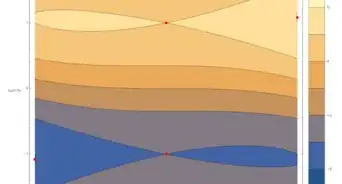
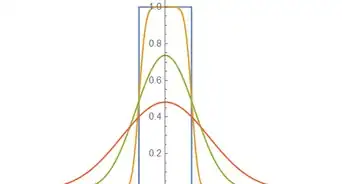
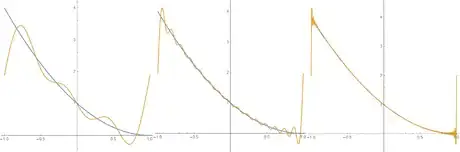
5Write out the function in terms of its Fourier series. This series converges on the interval Because the function is not periodic, the series does not hold on the whole interval, but rather in the neighborhood of any interior point (point-wise convergence as opposed to uniform convergence).
- The image shows the Fourier series up to and We can clearly see the convergence here, as well as the overshoots near the boundaries that do not seem to vanish at higher This is the Gibbs phenomenon, which is the result of the failure of the series to converge uniformly on the prescribed interval.
Advertisement
About This Article
Advertisement

![[-L,L].](./images/1400577721-4f521036855956b9219c60730f0ffca19238c1f0.webp)















![[-L,L],](./images/2005999622-e37c66242b2674fcddefd8f0fb6e3f50435200cd.webp)










![f(x)=x^{{2}}-2x+1:\ [-1,1]](./images/1793794074-e0749c3d357674d7fa287371ded07fc6f2ca6cdf.webp)













![x^{{2}}-2x+1={\frac {4}{3}}+\sum _{{n=1}}^{{\infty }}\left[{\frac {4(-1)^{{n}}}{n^{{2}}\pi ^{{2}}}}\cos n\pi x+{\frac {4(-1)^{{n}}}{n\pi }}\sin n\pi x\right]](./images/1729896339-35378d56599f81c6a24fde779af9d0fab33615e3.webp)