How to Calculate the Fourier Transform of a Function

Last Updated: September 28, 2022 References

The Fourier transform is an integral transform widely used in physics and engineering. They are widely used in signal analysis and are well-equipped to solve certain partial differential equations.

The convergence criteria of the Fourier transform (namely, that the function be absolutely integrable on the real line) are quite severe due to the lack of the exponential decay term as seen in the Laplace transform, and it means that functions like polynomials, exponentials, and trigonometric functions all do not have Fourier transforms in the usual sense. However, we can make use of the Dirac delta function to assign these functions Fourier transforms in a way that makes sense.

Because even the simplest functions that are encountered may need this type of treatment, it is recommended that you be familiar with the properties of the Laplace transform before moving on. Furthermore, it is more instructive to begin with the properties of the Fourier transform before moving on to more concrete examples.

Preliminaries

We define the Fourier transform of $f(t)$ $f(t)$ as the following function, provided the integral converges.^{[1]
X
Research source}
- ${\hat {f}}(\omega )={\mathcal {F}}\{f(t)\}=\int _{-\infty }^{\infty }f(t)e^{-i\omega t}\mathrm {d} t$
The inverse Fourier transform is defined in a similar manner. Notice the symmetry present between the Fourier transform and its inverse, a symmetry that is not present in the Laplace transform.^{[2]
X
Research source}
- $f(t)={\mathcal {F}}^{-1}\{{\hat {f}}(\omega )\}={\frac {1}{2\pi }}\int _{-\infty }^{\infty }{\hat {f}}(\omega )e^{i\omega t}\mathrm {d} \omega$
There are many other definitions of the Fourier transform. The above definition making use of angular frequency is one of them, and we will use this convention in this article. See the tips for two other commonly used definitions.
The Fourier transform and its inverse are linear operators, and therefore they both obey superposition and proportionality.^{[3]
X
Research source}
- $\int _{-\infty }^{\infty }[af(t)+bg(t)]e^{-i\omega t}\mathrm {d} t=a\int _{-\infty }^{\infty }f(t)e^{-i\omega t}\mathrm {d} t+b\int _{-\infty }^{\infty }g(t)e^{-i\omega t}\mathrm {d} t$

Part 1

Part 1 of 3:

Properties of the Fourier Transform

1
Determine the Fourier transform of a derivative. A simple integration by parts, coupled with the observation that $f(t)$ $f(t)$ must vanish at both infinities, yields the answer below.^{[4]
X
Research source}
- ${\begin{aligned}{\mathcal {F}}\{f^{\prime }(t)\}&=\int _{-\infty }^{\infty }f^{\prime }(t)e^{-i\omega t}\mathrm {d} t,\ \ u=e^{-i\omega t},\ v=f^{\prime }(t)\mathrm {d} t\\&=i\omega {\hat {f}}(\omega )\end{aligned}}$
- In general, we can take $n$ $n$ derivatives.
  - ${\mathcal {F}}\{f^{(n)}(t)\}=(i\omega )^{n}{\hat {f}}(\omega )$
- This yields the interesting property, stated below, which may be familiar in quantum mechanics as the form that the momentum operator takes in position space (on the left) and momentum space (on the right).^{[5]
  X
  Research source}
  - $-i{\frac {\mathrm {d} }{\mathrm {d} t}}\to \omega$
2
Determine the Fourier transform of a function multiplied by $t^{n}$ . The symmetry of the Fourier transform gives the analogous property in frequency space. We will first work with $n=1$ $n=1$ and then generalize.
- ${\begin{aligned}{\mathcal {F}}\{tf(t)\}&=\int _{-\infty }^{\infty }tf(t)e^{-i\omega t}\mathrm {d} t\\&=\int _{-\infty }^{\infty }i{\frac {\partial }{\partial \omega }}(e^{-i\omega t})f(t)\mathrm {d} t\\&=i{\frac {\mathrm {d} }{\mathrm {d} \omega }}{\hat {f}}(\omega )\end{aligned}}$
- In general, we can multiply by $t^{n}.$ $t^{{n}}.$
  - ${\mathcal {F}}\{t^{n}f(t)\}=i^{n}{\frac {\mathrm {d} ^{n}}{\mathrm {d} \omega ^{n}}}{\hat {f}}(\omega )$
- We immediately obtain the below result. This is a symmetry that is not fully realized with the Laplace transforms between the variables $t$ $t$ and $s.$ $s.$
  - $i{\frac {\mathrm {d} }{\mathrm {d} \omega }}\to t$
Advertisement
3
Determine the Fourier transform of a function multiplied by $e^{iat}$ . Multiplication by $e^{iat}$ $e^{{iat}}$ in the time domain corresponds to a shift in the frequency domain.^{[6]
X
Research source}
- ${\mathcal {F}}\{e^{iat}f(t)\}=\int _{-\infty }^{\infty }f(t)e^{-i(\omega -a)t}\mathrm {d} t={\hat {f}}(\omega -a)$
4
Determine the Fourier transform of a shifted function $f(t-c)$ . A shift in the time domain corresponds to multiplication by $e^{-i\omega c}$ $e^{{-i\omega c}}$ in the frequency domain, which again illustrates the symmetry between $t$ $t$ and $\omega .$ $\omega .$ We can easily evaluate this using a simple substitution.
- ${\begin{aligned}{\mathcal {F}}\{f(t-c)\}&=\int _{-\infty }^{\infty }f(t-c)e^{-i\omega t}\mathrm {d} t\\&=\int _{-\infty }^{\infty }f(t)e^{-i\omega (t+c)}\mathrm {d} t\\&=e^{-i\omega c}{\hat {f}}(\omega )\end{aligned}}$
5
Determine the Fourier transform of a stretched function $f(ct)$ . The stretch property seen in the Laplace transform also has an analogue in the Fourier transform.
- ${\begin{aligned}{\mathcal {F}}\{f(ct)\}&=\int _{-\infty }^{\infty }f(ct)e^{-i\omega t}\mathrm {d} t,\quad u=ct\\&={\frac {1}{|c|}}\int _{-\infty }^{\infty }f(u)e^{-i\omega u/c}\mathrm {d} u\\&={\frac {1}{|c|}}{\hat {f}}\left({\frac {\omega }{c}}\right)\end{aligned}}$
6
Determine the Fourier transform of a convolution of two functions. As with the Laplace transform, convolution in real space corresponds to multiplication in the Fourier space.^{[7]
X
Research source}
- ${\begin{aligned}{\mathcal {F}}\{f(t)*g(t)\}&=\int _{-\infty }^{\infty }e^{-i\omega t}\mathrm {d} t\int _{-\infty }^{\infty }f(t-y)g(y)\mathrm {d} y,\quad u=t-y\\&=\int _{-\infty }^{\infty }e^{-i\omega (u+y)}\mathrm {d} u\int _{-\infty }^{\infty }f(u)g(y)\mathrm {d} y\\&=\int _{-\infty }^{\infty }f(u)e^{-i\omega u}\mathrm {d} u\int _{-\infty }^{\infty }g(y)e^{-i\omega y}\mathrm {d} y\\&={\hat {f}}(\omega ){\hat {g}}(\omega )\end{aligned}}$
7
Determine the Fourier transform of even and odd functions. Even and odd functions have particular symmetries. We arrive at these results using Euler's formula and understanding how even and odd functions multiply. ^{[8]
X
Research source}
- The Fourier transform of an even function $f_{e}(t)$ $f_{{e}}(t)$ is also even, because the integral is even in $\omega$ $\omega$ due to the $\cos \omega t.$ $\cos \omega t.$ Furthermore, if $f_{e}(t)$ $f_{{e}}(t)$ is real, then its Fourier transform is also real.
  - ${\begin{aligned}{\mathcal {F}}\{f_{e}(t)\}&=\int _{-\infty }^{\infty }f_{e}(t)\left(\cos \omega t-i\sin \omega t\right)\mathrm {d} t\\&=2\int _{0}^{\infty }f_{e}(t)\cos \omega t\mathrm {d} t\end{aligned}}$
- The Fourier transform of an odd function $f_{o}(t)$ $f_{{o}}(t)$ is also odd, because the integral is odd in $\omega$ $\omega$ due to the $\sin \omega t.$ $\sin \omega t.$ Furthermore, if $f_{o}(t)$ $f_{{o}}(t)$ is real, then its Fourier transform is purely imaginary.
  - ${\begin{aligned}{\mathcal {F}}\{f_{o}(t)\}&=\int _{-\infty }^{\infty }f_{o}(t)\left(\cos \omega t-i\sin \omega t\right)\mathrm {d} t\\&=-2i\int _{0}^{\infty }f_{o}(t)\sin \omega t\mathrm {d} t\end{aligned}}$

Part 2

Part 2 of 3:

Fourier Transforms

1
Substitute the function into the definition of the Fourier transform. As with the Laplace transform, calculating the Fourier transform of a function can be done directly by using the definition. We will use the example function $f(t)={\frac {1}{t^{2}+1}},$ $f(t)={\frac {1}{t^{{2}}+1}},$ which definitely satisfies our convergence criteria.^{[9]
X
Research source}
- ${\mathcal {F}}\left\{{\frac {1}{t^{2}+1}}\right\}=\int _{-\infty }^{\infty }{\frac {e^{-i\omega t}}{t^{2}+1}}\mathrm {d} t$
2
Evaluate the integral using any means possible. This integral resists the techniques of elementary calculus, but we can make use of residue theory instead.^{[10]
X
Research source}
- To use residues, we create a contour $\gamma$ $\gamma$ consisting of a concatenation of the real line and a semicircular arc in the lower half plane that circles clockwise. The goal is to show that the real integral equals the contour integral by showing that the arc integral vanishes.
  - $\oint _{\gamma }{\frac {e^{-i\omega t}}{t^{2}+1}}\mathrm {d} t=\int _{-\infty }^{\infty }{\frac {e^{-i\omega t}}{t^{2}+1}}\mathrm {d} t+\int _{\text{arc}}{\frac {e^{-i\omega t}}{t^{2}+1}}\mathrm {d} t$
- We may factor the denominator to show that the function has simple poles at $t_{\pm }=\pm i.$ $t_{{\pm }}=\pm i.$ Since only $t_{-}$ $t_{{-}}$ is being enclosed, we can use the residue theorem to calculate the value of the contour integral.
  - $\operatorname {Res} (f(t);-i)={\frac {e^{-\omega }}{-2i}}$
- Note that since our contour is in the clockwise direction, there is an additional negative sign.
  - $\oint _{\gamma }{\frac {e^{-i\omega t}}{t^{2}+1}}\mathrm {d} t=-2\pi i\cdot {\frac {e^{-\omega }}{-2i}}=\pi e^{-\omega }$
- Equally important is the process in showing that the arc integral vanishes. Jordan's lemma aids in this evaluation. While the lemma does not say that the integral vanishes, it does bound the difference between the contour integral and the real integral.^{[11]
  X
  Research source
  www.damtp.cam.ac.uk/user/reh10/lectures/nst-mmii-chapter5.pdf} We apply the lemma to the lower half plane below for a function $f(t)=e^{-i\omega t}g(t),$ $f(t)=e^{{-i\omega t}}g(t),$ where $\omega >0.$ $\omega >0.$ Given a parameterization $C=Re^{-i\phi }$ $C=Re^{{-i\phi }}$ where $\phi \in [0,\pi ],$ $\phi \in [0,\pi ],$ then Jordan's lemma prescribes the following bound of the integral:
  - ${\Bigg |}\int _{C}f(t)\mathrm {d} t{\Bigg |}\leq {\frac {\pi }{\omega }}\max _{\phi \in [0,\pi ]}g(Re^{-i\phi })$
- Now, all we need to do is show that $g(t)$ $g(t)$ vanishes in the large $R$ $R$ limit, which is trivial here because the function falls off as $1/R^{2}.$ $1/R^{{2}}.$
  - $\lim _{R\to \infty }{\frac {1}{(Re^{-i\phi })^{2}+1}}=0$
- What is the domain of $\omega$ $\omega$ in this result? As stated previously, Jordan's lemma only applies for $\omega >0.$ $\omega >0.$ However, when one repeats this calculation by enclosing the upper half plane, finding the residue at the other pole, and applying Jordan's lemma again to ensure the arc integral vanishes, the result will be $\pi e^{\omega }$ $\pi e^{{\omega }}$ while the domain of $\omega$ $\omega$ will be the negative reals. So the final answer is written below.
  - ${\mathcal {F}}\left\{{\frac {1}{t^{2}+1}}\right\}=\pi e^{-|\omega |}$
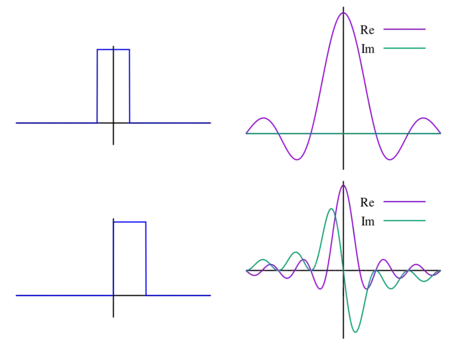
3
Evaluate the Fourier transform of the rectangular function. The rectangular function $\operatorname {rect} (t),$ $\operatorname {rect}(t),$ or the unit pulse, is defined as a piecewise function that equals 1 if $-{\frac {1}{2}}<t<{\frac {1}{2}},$ $-{\frac {1}{2}}<t<{\frac {1}{2}},$ and 0 everywhere else. As such, we can evaluate the integral over just these bounds. The result is the cardinal sine function.
- ${\begin{aligned}{\mathcal {F}}\{\operatorname {rect} (t)\}&=\int _{-1/2}^{1/2}e^{-i\omega t}\mathrm {d} t\\&={\frac {1}{i\omega }}\left(e^{i\omega /2}-e^{-i\omega /2}\right)\\&={\frac {2}{\omega }}\sin {\frac {\omega }{2}}\end{aligned}}$
- If the unit pulse is shifted such that the bounds are 0 and 1, then there exists an imaginary component as well, as seen by the graph above. This is due to the fact that the function is no longer even.
  - $\int _{0}^{1}e^{-i\omega t}\mathrm {d} t={\frac {\sin \omega }{\omega }}+i\left({\frac {\cos \omega -1}{\omega }}\right)$
4
Evaluate the Fourier transform of the Gaussian function. The Gaussian function is one of the few functions that is its own Fourier transform. We integrate by completing the square.^{[12]
X
Research source}
- ${\begin{aligned}{\mathcal {F}}\{e^{-t^{2}}\}&=\int _{-\infty }^{\infty }e^{-t^{2}}e^{-i\omega t}\mathrm {d} t\\&=\int _{-\infty }^{\infty }e^{-(t^{2}+i\omega t-\omega ^{2}/4+\omega ^{2}/4)}\mathrm {d} t\\&=e^{-\omega ^{2}/4}\int _{-\infty }^{\infty }e^{-(t+i\omega /2)^{2}}\mathrm {d} t\\&={\sqrt {\pi }}e^{-\omega ^{2}/4}\end{aligned}}$

Part 3

Part 3 of 3:

Distributions

1
Evaluate the Fourier transform of $e^{iat}$ . If you have had some exposure to Laplace transforms before, you know that the exponential function is the "simplest" function that has a Laplace transform. In the case of the Fourier transform, this function is not well-behaved because the modulus of this function does not tend to 0 as $t\to \infty .$ $t\to \infty .$ Nevertheless, its Fourier transform is given as the delta function.
- ${\mathcal {F}}\{e^{iat}\}=2\pi \delta (\omega -a)$
- The imaginary exponential oscillates around the unit circle, except when $t=0,$ where the exponential equals 1. You can think of the contributions by the oscillations as canceling themselves out for all $t\neq 0.$ At $t=0,$ the integral of the function then diverges. The delta function is then used to model this behavior.
- This result gives us the Fourier transform of three other functions for "free." The Fourier transform of the constant function is obtained when we set $a=0.$ $a=0.$
  - ${\mathcal {F}}\{1\}=2\pi \delta (\omega )$
- The Fourier transform of the delta function is simply 1.
  - ${\mathcal {F}}\{\delta (t)\}=1$
- Using Euler's formula, we get the Fourier transforms of the cosine and sine functions.^{[13]
  X
  Research source}
  - ${\mathcal {F}}\{\cos at\}=\pi (\delta (\omega -a)+\delta (\omega +a))$
  - ${\mathcal {F}}\{\sin at\}=-i\pi (\delta (\omega -a)-\delta (\omega +a))$
2
Evaluate the Fourier transform of $t^{n}e^{iat}$ . We can use the shift property to compute Fourier transforms of powers, and therefore all polynomials. Note that this involves computing derivatives of the delta function.
- ${\mathcal {F}}\{t^{n}e^{iat}\}=2\pi i^{n}{\frac {\mathrm {d} ^{n}}{\mathrm {d} \omega ^{n}}}\delta (\omega -a)$
3
Evaluate the Fourier transform of the Heaviside step function. The Heaviside function $\Theta (t)$ $\Theta (t)$ is the function that equals $0$ $0$ for negative $t$ $t$ and $1$ $1$ for positive $t.$ $t.$ ^{[14]
X
Research source} As with the delta function, $\Theta (t)$ $\Theta (t)$ does not have a Fourier transform in the usual sense because $\Theta (t)$ $\Theta (t)$ is not absolutely integrable. Ignoring this warning, we can write out its Fourier transform by naively doing the integral.
- ${\mathcal {F}}\{\Theta (t)\}=\int _{0}^{\infty }e^{-i\omega t}\mathrm {d} t={\frac {e^{-i\omega t}}{-i\omega }}{\Bigg |}_{0}^{\infty }={\frac {1}{i\omega }}$
- In order to make sense of this answer, we appeal to convolutions. The derivative of a convolution of two functions is given below. Note that this is not the product rule of ordinary derivatives.
  - ${\frac {\mathrm {d} }{\mathrm {d} t}}(f(t)*g(t))=f'*g=f*g'$
- Then, we see that the convolution of the derivative of an absolutely integrable function $f(t)$ $f(t)$ with $\Theta (t)$ $\Theta (t)$ can be written in the following manner. This also implies the important relation $\Theta '(t)=\delta (t).$ $\Theta '(t)=\delta (t).$
  - ${\begin{aligned}f'(t)*\Theta (t)&=\int _{-\infty }^{\infty }f'(y)\Theta (t-y)\mathrm {d} y\\&=\int _{-\infty }^{t}f'(y)\mathrm {d} y=f(t)\end{aligned}}$
  - ${\mathcal {F}}\{f'(t)*\Theta (t)\}={\hat {f}}(\omega )={\hat {f}}'(\omega ){\hat {\Theta }}(\omega )=i\omega {\hat {f}}(\omega ){\hat {\Theta }}(\omega )$
- In this sense, we may then conclude that ${\mathcal {F}}\{\Theta (t)\}={\frac {1}{i\omega }}.$