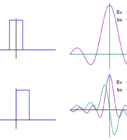How to Integrate Gaussian Functions

Last Updated: July 31, 2020

The Gaussian function $f(x)=e^{-x^{2}}$ is one of the most important functions in mathematics and the sciences. Its characteristic bell-shaped graph comes up everywhere from the normal distribution in statistics to position wave packets of a particle in quantum mechanics.

Integrating this function over all of $x$ is an extremely common task, but it resists the techniques of elementary calculus. No amount of change of variables, integration by parts, trigonometric substitution, etc. will simplify the integral. In fact, the antiderivative of the Gaussian, the error function, cannot be written in terms of elementary functions. Nevertheless, there exists an exact solution for the definite integral, which we find in this article. We also generalize the Gaussian integral to obtain some more interesting results. These generalizations require some more techniques such as differentiating under the integral and knowledge of the Gamma function.

Part 1

Part 1 of 3:

Gaussian Integral

1
Begin with the integral.
- $\int _{-\infty }^{\infty }e^{-x^{2}}\mathrm {d} x$
2
Consider the square of the integral. We are expanding this integral into the $xy$ $xy$ plane. The idea here is to turn this problem into a double integral for which we can easily solve, and then take the square root.
- $\int _{-\infty }^{\infty }\mathrm {d} xe^{-x^{2}}\int _{-\infty }^{\infty }\mathrm {d} ye^{-y^{2}}$
Advertisement
3
Convert to polar coordinates. Recall that the area integral of a polar rectangle is of the form $r\mathrm {d} r\mathrm {d} \theta ,$ $r{\mathrm {d}}r{\mathrm {d}}\theta ,$ with the extra $r$ $r$ there in order to scale the angle to units of length. This extra $r$ $r$ makes the integrals trivial since we can identify $r^{2}=x^{2}+y^{2}.$ $r^{{2}}=x^{{2}}+y^{{2}}.$
- ${\begin{aligned}\int _{-\infty }^{\infty }\mathrm {d} xe^{-x^{2}}\int _{-\infty }^{\infty }\mathrm {d} ye^{-y^{2}}&=\int _{-\infty }^{\infty }\mathrm {d} x\int _{-\infty }^{\infty }\mathrm {d} ye^{-(x^{2}+y^{2})}\\&=\int _{0}^{\infty }r\mathrm {d} r\int _{0}^{2\pi }\mathrm {d} \theta e^{-r^{2}}\end{aligned}}$
4
Evaluate by means of a u-substitution. Let $u=r^{2}.$ $u=r^{{2}}.$ Then the differential $\mathrm {d} u=2r\mathrm {d} r$ ${\mathrm {d}}u=2r{\mathrm {d}}r$ will cancel out the extra $r$ $r$ that we got from changing to polar. Since the integrand has no $\theta$ $\theta$ dependence, we can evaluate the $\theta$ $\theta$ integral immediately.
- ${\begin{aligned}\int _{0}^{\infty }r\mathrm {d} r\int _{0}^{2\pi }\mathrm {d} \theta e^{-r^{2}}&=2\pi \int _{0}^{\infty }re^{-r^{2}}\mathrm {d} r,\quad u=r^{2}\\&=\pi \int _{0}^{\infty }e^{-u}\mathrm {d} u\\&=\pi (-e^{-\infty }+e^{0})\\&=\pi \end{aligned}}$
5
Arrive at the integral of a Gaussian. Since we were evaluating the square of the integral, we take the square root of our result.
- $\int _{-\infty }^{\infty }e^{-x^{2}}\mathrm {d} x={\sqrt {\pi }}$
- Importantly, the Gaussian function is even.
  - $\int _{-\infty }^{\infty }e^{-x^{2}}\mathrm {d} x=2\int _{0}^{\infty }e^{-x^{2}}\mathrm {d} x=2\cdot {\frac {\sqrt {\pi }}{2}}$
6
Consider the integral of the general Gaussian function. This function is determined by the parameters $a$ $a$ and $\sigma ,$ $\sigma ,$ where $a$ $a$ is a (normalization) constant that determines the height of the bell curve, and $\sigma$ $\sigma$ is the standard deviation, which determines the curve's width.
- $f(x)=ae^{-{\frac {x^{2}}{2\sigma ^{2}}}}$
- Follow the steps shown above to verify this integral.
  - $\int _{-\infty }^{\infty }ae^{-{\frac {x^{2}}{2\sigma ^{2}}}}\mathrm {d} x=a\sigma {\sqrt {2\pi }}$
- Another way to formulate the problem is if we have a Gaussian in the form $e^{-\alpha x^{2}}.$ $e^{{-\alpha x^{{2}}}}.$ Verify this integral as well.
  - $\int _{-\infty }^{\infty }e^{-\alpha x^{2}}\mathrm {d} x={\sqrt {\frac {\pi }{\alpha }}}$
7
(Optional) Normalize the area to find the normalization constant $a$ . In many applications, it is desired that the area of the Gaussian be set to unity. In this case, we set $a\sigma {\sqrt {2\pi }}=1$ $a\sigma {\sqrt {2\pi }}=1$ and solve for $a.$ $a.$
- $a={\frac {1}{\sigma {\sqrt {2\pi }}}}$
- Here, we arrive at the normalized Gaussian, so desired in such applications as probability theory and quantum mechanics.
  - $f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {x^{2}}{2\sigma ^{2}}}}$

Part 2

Part 2 of 3:

Generalizations

1
Consider the integral below. The Gaussian integral $\int _{0}^{\infty }e^{-\alpha x^{2}}\mathrm {d} x={\frac {1}{2}}{\sqrt {\frac {\pi }{\alpha }}}$ $\int _{{0}}^{{\infty }}e^{{-\alpha x^{{2}}}}{\mathrm {d}}x={\frac {1}{2}}{\sqrt {{\frac {\pi }{\alpha }}}}$ is a result that can be used to find numerous related integrals. The ones below are called moments of the Gaussian. Below, $n$ $n$ is a positive number.
- $\int _{0}^{\infty }x^{n}e^{-x^{2}}\mathrm {d} x$
2
If $n$ is even, consider the related integral (written below) and differentiate under the integral. The result from differentiating under the integral is that even powers of $x$ $x$ get brought down. Notice that as the integral gets negated, the result on the right also gets negated because of the negative power in $\alpha ,$ $\alpha ,$ so the answers remain positive. Since differentiation is much easier than integration, we could do this all day, making sure to set $\alpha =1$ $\alpha =1$ at a convenient time. We list some of these integrals below. Make sure to verify them for yourself.
- $\int _{0}^{\infty }e^{-\alpha x^{2}}\mathrm {d} x={\frac {1}{2}}{\sqrt {\frac {\pi }{\alpha }}}$
- $\int _{0}^{\infty }x^{2}e^{-x^{2}}\mathrm {d} x=-\int _{0}^{\infty }{\frac {\partial }{\partial \alpha }}e^{-\alpha x^{2}}\mathrm {d} x=-{\frac {\mathrm {d} }{\mathrm {d} \alpha }}\left({\frac {1}{2}}{\sqrt {\frac {\pi }{\alpha }}}\right)={\frac {\sqrt {\pi }}{4}}$
- $\int _{0}^{\infty }x^{4}e^{-x^{2}}\mathrm {d} x={\frac {3{\sqrt {\pi }}}{8}}$
- $\int _{0}^{\infty }x^{6}e^{-x^{2}}\mathrm {d} x={\frac {15{\sqrt {\pi }}}{16}}$
3
If $n$ is not even, use the u-sub $u=x^{2}$ . Then we can use the Gamma function to easily evaluate. Below, we choose $n=9$ $n=9$ and $n=1/3$ $n=1/3$ as examples.
- $\int _{0}^{\infty }x^{9}e^{-x^{2}}\mathrm {d} x={\frac {1}{2}}\int _{0}^{\infty }u^{4}e^{-u}\mathrm {d} u={\frac {4!}{2}}=12$
- $\int _{0}^{\infty }x^{1/3}e^{-x^{2}}\mathrm {d} x={\frac {1}{2}}\int _{0}^{\infty }u^{-1/3}e^{-u}\mathrm {d} u={\frac {\Gamma (2/3)}{2}}$
- It is interesting to note that we could've used the Gamma function for even $n$ as well. It is a more general method of evaluating these types of integrals that typically is no more involved than differentiating under the integral.
4
Set $\alpha =i$ to obtain three integrals. The result is general enough such that $\alpha$ $\alpha$ can even take on complex values, as long as $\operatorname {Re} (\alpha )\geq 0.$ $\operatorname {Re}(\alpha )\geq 0.$ Recall Euler's formula relating the complex exponential function to the trigonometric functions. If we take the real and imaginary parts of our result, we obtain two integrals for free. Neither of the two real integrals have antiderivatives that can be written in closed form.
- $e^{-ix^{2}}=\cos x^{2}-i\sin x^{2}$
- $\int _{0}^{\infty }e^{-ix^{2}}\mathrm {d} x={\frac {1}{2}}{\sqrt {\frac {\pi }{i}}}={\frac {\sqrt {\pi }}{2}}e^{-i\pi /4}={\frac {\sqrt {\pi }}{2{\sqrt {2}}}}(1-i)$
- $\int _{0}^{\infty }\cos x^{2}\mathrm {d} x=\int _{0}^{\infty }\sin x^{2}\mathrm {d} x={\frac {\sqrt {\pi }}{2{\sqrt {2}}}}$
- These two integrals are special cases of the Fresnel integrals, where they are important in the study of optics.
- If you are not very familiar with complex numbers, the number $i$ can be rewritten in polar form as $e^{i\pi /2},$ because imaginary exponents are rotations in the complex plane - in this case, by an angle of $\pi /2.$ Polar form simplifies almost everything associated with complex numbers, so we can easily take the square root.
5
Calculate the Fourier transform of the Gaussian function by completing the square. Calculating the Fourier transform is computationally very simple, but it requires a slight modification. We opt to complete the square because we recognize the property that the integral is independent of the shift (see the discussion). Since we have to add 0 in order to not change the integrand, we have to compensate by adding a $-{\frac {\omega ^{2}}{4}}$ $-{\frac {\omega ^{{2}}}{4}}$ term. Watch the signs - they can be tricky.
- ${\begin{aligned}{\mathcal {F}}\{e^{-t^{2}}\}&=\int _{-\infty }^{\infty }e^{-t^{2}}e^{-i\omega t}\mathrm {d} t\\&=\int _{-\infty }^{\infty }e^{-(t^{2}+i\omega t-\omega ^{2}/4+\omega ^{2}/4)}\mathrm {d} t\\&=e^{-\omega ^{2}/4}\int _{-\infty }^{\infty }e^{-(t+i\omega /2)^{2}}\mathrm {d} t\\&={\sqrt {\pi }}e^{-\omega ^{2}/4}\end{aligned}}$
- Interestingly, the Fourier transform of a Gaussian is another (scaled) Gaussian, a property that few other functions have (the hyperbolic secant, whose function is also shaped like a bell curve, is also its own Fourier transform).
- This technique of completing the square can also be used to find integrals like the ones below. Verify this by considering the "complexified" expression $e^{i\alpha x/\beta }$ $e^{{i\alpha x/\beta }}$ and then taking the real part of the result.
  - $\int _{-\infty }^{\infty }\cos {\frac {\alpha x}{\beta }}e^{-x^{2}}\mathrm {d} x={\sqrt {\pi }}e^{-\alpha ^{2}/4\beta ^{2}}$

Part 3

Part 3 of 3:

Error Function

1
Define the error function. It is often the case that the Gaussian integral needs to be evaluated across the real line. However, many other applications, such as in diffusion and statistics, require a more general relationship.
- Because the Gaussian function does not have an antiderivative that can be written in terms of elementary functions, we define the error function $\operatorname {erf} (x)$ $\operatorname {erf}(x)$ as the antiderivative of the Gaussian. It is a special function conventionally defined with a normalization factor ensuring a range of $x\in (-1,1).$ $x\in (-1,1).$ It has a sigmoid shape similar in form to the logistic function.
  - $\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\mathrm {d} t$
- It is also convenient to define the complementary error function as well.
  - $\operatorname {erfc} (x)=1-\operatorname {erf} (x)$
- It should be noted that the act of defining this special function does not give new insights or fundamental forays into mathematics. It is merely a definition of a function that happens to be encountered often enough to be given its own name.
2
Solve the one-dimensional heat equation given initial conditions. As an example of an application requiring the use of the error function, we solve the heat equation using Fourier transforms with the initial conditions being the rectangular function. Below, $\alpha$ $\alpha$ is known as the diffusion coefficient.
- ${\frac {\partial u}{\partial t}}-\alpha {\frac {\partial ^{2}u}{\partial x^{2}}}=0$
- $u(x,0)=u_{0}(x)={\begin{cases}1&|x|\leq 1/2\\0&|x|>1/2\end{cases}}$
3
Find the fundamental solution. The fundamental solution $U(x,t)$ $U(x,t)$ is the solution to the heat equation given initial conditions of a point source, the Dirac delta function. The fundamental solution in this context is also known as the heat kernel.
- We perform a Fourier transform to convert from real space to $\xi$ $\xi$ space to obtain an ordinary differential equation in $t.$ $t.$ Then we simply solve for ${\hat {u}}(\xi ,t).$ ${\hat {u}}(\xi ,t).$ The useful property of the Fourier transform that we take advantage of here is that the Fourier transform of a derivative of order $n$ $n$ corresponds to multiplication of $(i\xi )^{n}$ $(i\xi )^{{n}}$ in $\xi$ $\xi$ space.
  - ${\frac {\partial {\hat {u}}}{\partial t}}+\alpha \xi ^{2}{\hat {u}}=0$
- The additional constant simply corresponds to initial conditions.
  - ${\hat {u}}(\xi ,t)={\hat {u}}_{0}(\xi )e^{-\alpha \xi ^{2}t}$
- Now we have to transform back into real space. This is convenient for us because multiplication in $\xi$ $\xi$ space corresponds to convolution in real space. The fundamental solution is then simply the inverse Fourier transform of the exponential term, shown below. It is deemed the fundamental solution because the delta function is the identity operator of convolution: $\delta (x)*U(x,t)=U(x,t).$ $\delta (x)*U(x,t)=U(x,t).$
  - $u(x,t)=u_{0}(x)*{\mathcal {F}}^{-1}\left\{e^{-\alpha \xi ^{2}t}\right\}$
- We have already seen how to calculate the Fourier transform of a Gaussian function. We apply the technique of completing the square here too.
- ${\begin{aligned}U(x,t)&={\mathcal {F}}^{-1}\left\{e^{-\alpha \xi ^{2}t}\right\}\\&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{-\alpha \xi ^{2}t}e^{ix\xi }\mathrm {d} \xi \\&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{-\alpha t\left(\xi ^{2}-2{\frac {ix\xi }{2\alpha t}}-{\frac {x^{2}}{4\alpha ^{2}t^{2}}}\right)}e^{-x^{2}/4\alpha t}\mathrm {d} \xi \\&={\frac {1}{2\pi }}e^{-x^{2}/4\alpha t}\int _{-\infty }^{\infty }e^{-\alpha t\left(\xi -{\frac {ix}{2\alpha t}}\right)^{2}}\mathrm {d} \xi \\&={\frac {1}{\sqrt {4\pi \alpha t}}}e^{-x^{2}/4\alpha t}\end{aligned}}$
4
Solve for $u(x,t)$ given initial conditions. Now that we have our fundamental solution $U(x,t),$ $U(x,t),$ we can take the convolution of $U(x,t)$ $U(x,t)$ with $u_{0}(x).$ $u_{{0}}(x).$
- ${\begin{aligned}u(x,t)&=u_{0}(x)*U(x,t)=\int _{-\infty }^{\infty }u_{0}(y)U(x-y,t)\mathrm {d} y\\&={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{-1/2}^{1/2}e^{-(x-y)^{2}/4\alpha t}\mathrm {d} y\\&={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{-1/2-x}^{1/2-x}e^{-\left({\frac {z}{\sqrt {4\alpha t}}}\right)^{2}}\mathrm {d} z\\&={\frac {1}{2}}\left[\operatorname {erf} \left({\frac {1/2-x}{\sqrt {4\alpha t}}}\right)-\operatorname {erf} \left({\frac {-1/2-x}{\sqrt {4\alpha t}}}\right)\right]\end{aligned}}$
- In the last step, we make use of the fact that $\int e^{-x^{2}}\mathrm {d} x={\frac {\sqrt {\pi }}{2}}\operatorname {erf} (x).$
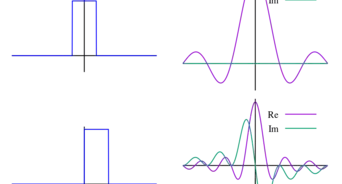
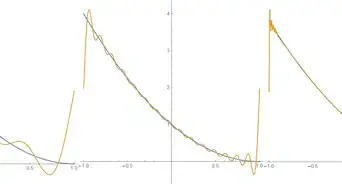
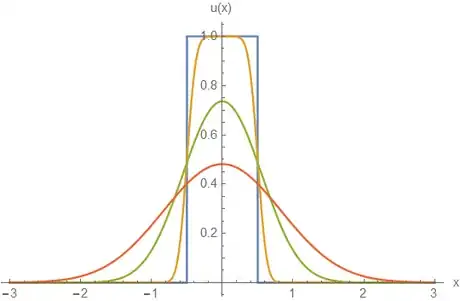
- A plot of this function over time above shows that the "sharpness" of the function diminishes over time, eventually tending towards an equilibrium solution. The initial conditions are plotted in blue, while $u(x,t)$ is being plotted for values $t=0.005,$ $t=0.1,$ and $t=0.3,$ for orange, green, and red plots, respectively.
- We see from the graph that the function is sharply sloped near $x=\pm 1/2,$ which the error function takes care of. However, the error function is still a continuous, well-behaved function, so this solution cannot exist at the moment $t=0,$ when the argument inside the error function becomes singular and when the function approaches the discontinuous $u_{0}(x)$ defined earlier.

Discussion

It turns out that the Gaussian as defined in step 6 of part 1 is not the most general form. As seen in the diagram, one can also shift the Gaussian some units $\mu ,$ $\mu ,$ so that the $x^{2}$ $x^{{2}}$ turns into a $(x-\mu )^{2}$ $(x-\mu )^{{2}}$ in the exponent. However, it is obvious that the translation does not matter when we are integrating over all $x,$ $x,$ which is why completing the square while calculating the Fourier transform works. Nevertheless, the general form of the normalized Gaussian looks like this.
- $f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$