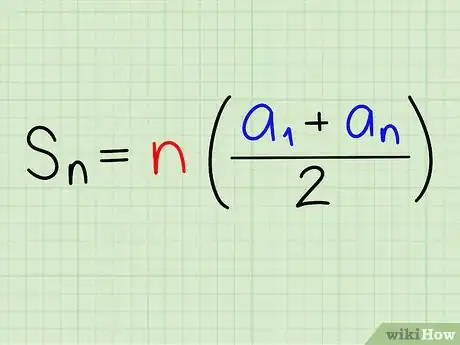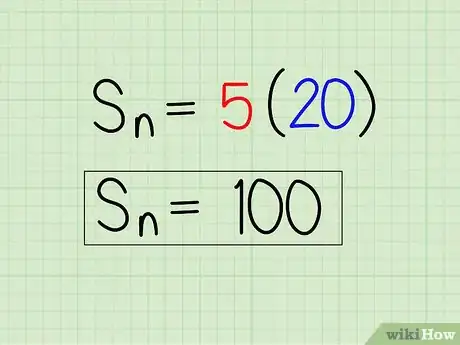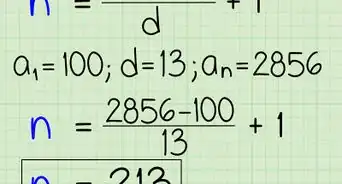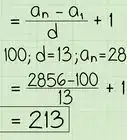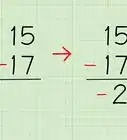How to Find the Sum of an Arithmetic Sequence

Co-authored by wikiHow Staff

Last Updated: September 2, 2022 References

An arithmetic sequence is a series of numbers in which each term increases by a constant amount. To sum the numbers in an arithmetic sequence, you can manually add up all of the numbers. This is impractical, however, when the sequence contains a large amount of numbers. Instead, you can quickly find the sum of any arithmetic sequence by multiplying the average of the first and last term by the number of terms in the sequence.

Part 1

Part 1 of 3:

Assessing Your Sequence

1
Make sure you have an arithmetic sequence. An arithmetic sequence is an ordered series of numbers, in which the change in numbers is constant.^{[1]
X
Research source} This method only works if your set of numbers is an arithmetic sequence.
- To determine whether you have an arithmetic sequence, find the difference between the first few and the last few numbers. Ensure that the difference is always the same.
- For example, the series 10, 15, 20, 25, 30 is an arithmetic sequence, because the difference between each term is constant (5).
2
Identify the number of terms in your sequence. Each number is a term. If there are only a few terms listed, you can count them. Otherwise, if you know the first term, last term, and common difference (the difference between each term) you can use a formula to find the number of terms. Let this number be represented by the variable $n$ $n$ .
- For example, if you are calculating the sum of the sequence 10, 15, 20, 25, 30, $n=5$ , since there are 5 terms in the sequence.
Advertisement
3
Identify the first and last terms in the sequence. You need to know both of these numbers in order to calculate the sum of the arithmetic sequence. Often the first numbers will be 1, but not always. Let the variable $a_{1}$ $a_{{1}}$ equal the first term in the sequence, and $a_{n}$ $a_{{n}}$ equal the last term in the sequence.
- For example, in the sequence 10, 15, 20, 25, 30 $a_{1}=10$ , and $a_{n}=30$ .

Part 2

Part 2 of 3:

Calculating the Sum

1
Set up the formula for finding the sum of an arithmetic sequence. The formula is $S_{n}=n({\frac {a_{1}+a_{n}}{2}})$ $S_{{n}}=n({\frac {a_{{1}}+a_{{n}}}{2}})$ , where $S_{n}$ $S_{{n}}$ equals the sum of the sequence.^{[2]
X
Research source}
- Note that this formula is indicating that the sum of the arithmetic sequence is equal to the average of the first and last term, multiplied by the number of terms.^{[3]
  X
  Research source}
2
Plug the values of $n$ , $a_{1}$ , and $a_{n}$ into the formula. Make sure you make the correct substitutions.^{[4]
X
Research source}
- For example, if you have 5 terms in your sequence, and 10 is the first term, and 30 is the last term, your formula will look like this: $S_{n}=5({\frac {10+30}{2}})$ .
3
Calculate the average of the first and second term. To do this, add the two numbers, and divide by 2.^{[5]
X
Research source}
- For example:
  $S_{n}=5({\frac {40}{2}})$
  $S_{n}=5(20)$
4
Multiply the average by the number of terms in the series. This will give you the sum of the arithmetic sequence.^{[6]
X
Research source}
- For example:
  $S_{n}=5(20)$
  $S_{n}=100$
  So, the sum of the sequence 10, 15, 20, 25, 30 is 100.

Part 3

Part 3 of 3:

Completing Sample Problems

1
Find the sum of numbers between 1 and 500. Consider all consecutive integers.
- Determine the number of terms ( $n$ ) in the sequence. Since you are considering all consecutive integers to 500, $n=500$ .
- Determine the first ( $a_{1}$ ) and last ( $a_{n}$ ) terms in the sequence. Since the sequence is 1 to 500, $a_{1}=1$ and $a_{n}=500$ .
- Find the average of $a_{1}$ and $a_{n}$ : ${\frac {1+500}{2}}=250.5$ .
- Multiply the average by $n$ : $250.5\times 500=125,250$ .
2
Find the sum of the described arithmetic sequence. The first term in the sequence is 3. The last term in the sequence is 24. The common difference is 7.
- Determine the number of terms ( $n$ ) in the sequence. Since you begin with 3, end with 24, and go up by 7 each time, the series is 3, 10, 17, 24. (The common difference is the difference between each term in the sequence.)^{[7]
  X
  Research source} This means that $n=4$
- Determine the first ( $a_{1}$ ) and last ( $a_{n}$ ) terms in the sequence. Since the sequence is 3 to 24, $a_{1}=3$ and $a_{n}=24$ .
- Find the average of $a_{1}$ and $a_{n}$ : ${\frac {3+24}{2}}=13.5$ .
- Multiply the average by $n$ : $13.5\times 4=54$ .
3
Solve the following problem. Mara saves 5 dollars the first week of the year. For the rest of the year, she increases her weekly savings by 5 dollars every week. How much money does Mara save by the end of the year?
- Determine the number of terms ( $n$ ) in the sequence. Since Mara save for 52 weeks (1 year), $n=52$ .
- Determine the first ( $a_{1}$ ) and last ( $a_{n}$ ) terms in the sequence. The first amount she saves is 5 dollars, so $a_{1}=5$ . To find out the amount she saves the last week of the year, calculate $5\times 52=260$ . So $a_{n}=260$ .
- Find the average of $a_{1}$ and $a_{n}$ : ${\frac {5+260}{2}}=132.5$ .
- Multiply the average by $n$ : $132.5\times 52=6,890$ . So she saves $6,890 by the end of the year.

Community Q&A

Question

How can I determine whether the sequence is arithmetic?

Donagan

Top Answerer

A sequence is arithmetic if there is a constant difference between any term and the terms immediately before and after it: for example, if each term is 7 more than the term before it.
Question

Why do I need to divide by 2?

Community Answer

You do this so that you can find the average of the two numbers. For example, if you were finding the average between 7, 12, and 8, you would add them up (27) and divide them by the number of values you have. In this case, you have three numbers, so you'd divide 27 by 3 to get an average of 9. In the case of the sum of an arithmetic sequence, you have two numbers that you are finding the average of, so you divide it by the amount of values you have, which is two.
Question

What is the sum of all integers from 1 to 50?

LyKaxandra Caimoy

Community Answer

You will find that 1 + 50 = 2 + 49 = 3 + 48 (and so on). Multiply the sum, which is 51, by half of the last term. You have the equation 51 × 25 = 1275. The sum is therefore 1275.