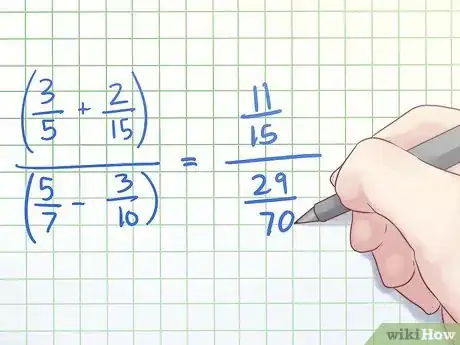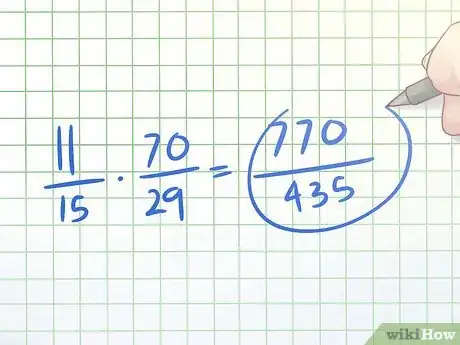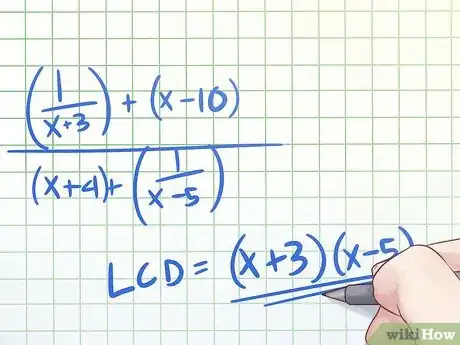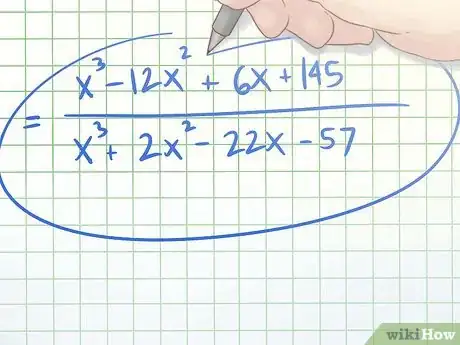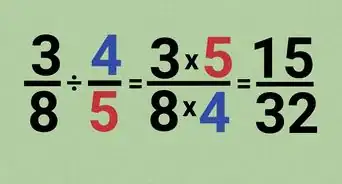How to Simplify Complex Fractions

Co-authored by David Jia

Last Updated: October 10, 2022

Complex fractions are fractions in which either the numerator, denominator, or both contain fractions themselves. For this reason, complex fractions are sometimes referred to as "stacked fractions". Simplifying complex fractions is a process that can range from easy to difficult based on how many terms are present in the numerator and denominator, whether any of the terms are variables, and, if so, the complexity of the variable terms. See Step 1 below to get started!

Method 1

Method 1 of 2:

Simplifying Complex Fractions with Inverse Multiplication

1
If necessary, simplify the numerator and denominator into single fractions. Complex fractions aren't necessarily difficult to solve. In fact, complex fractions in which the numerator and denominator both contain a single fraction are usually fairly easy to solve. So, if the numerator or denominator of your complex fraction (or both) contain multiple fractions or fractions and whole numbers, simplify as needed to obtain a single fraction in both the numerator and denominator. This may require finding the least common denominator (LCM) of two or more fractions.
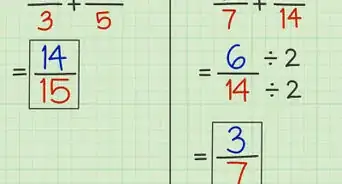
- For example, let's say we want to simplify the complex fraction (3/5 + 2/15)/(5/7 - 3/10). First, we would simplify both the numerator and denominator of our complex fraction to single fractions.
  - To simplify the numerator, we will use a LCM of 15 by multiplying 3/5 by 3/3. Our numerator becomes 9/15 + 2/15, which equals 11/15.
  - To simplify the denominator, we will use a LCM of 70 by multiplying 5/7 by 10/10 and 3/10 by 7/7. Our denominator becomes 50/70 - 21/70, which equals 29/70.
  - Thus, our new complex fraction is (11/15)/(29/70).
2
Flip the denominator to find its inverse. By definition, dividing one number by another is the same as multiplying the first number by the inverse of the second. Now that we have obtained a complex fraction with a single fraction in both the numerator and the denominator, we can use this property of division to simplify our complex fraction! First, find the inverse of the fraction on the bottom of the complex fraction. Do this by "flipping" the fraction - setting its numerator in the place of the denominator and vice versa.
- In our example, the fraction in the denominator of the complex fraction (11/15)/(29/70) is 29/70. To find its inverse, we simply "flip" it to get 70/29.
  - Note that, if your complex fraction has a whole number in its denominator, you can treat it as a fraction and find its inverse all the same. For instance, if our complex fraction was (11/15)/(29), we can define the denominator as 29/1, which makes its inverse 1/29.
Advertisement
3
Multiply the numerator of the complex fraction by the inverse of the denominator. Now that you've obtained the inverse of your complex fraction's denominator, multiply it by the numerator to obtain a single simple fraction! Remember that to multiply two fractions, we simply multiply across - the numerator of the new fraction is the product of the numerators of the two old ones, and similarly with the denominator.
- In our example, we would multiply 11/15 × 70/29. 70 × 11 = 770 and 15 × 29 = 435. So, our new simple fraction is 770/435.
4
Simplify the new fraction by finding the greatest common factor. We now have a single, simple fraction, so all that remains is to render it in the simplest terms possible. Find the greatest common factor (GCF) of the numerator and denominator and divide both by this number to simplify.
- One common factor of 770 and 435 is 5. So, if we divide the numerator and denominator of our fraction by 5, we obtain 154/87. 154 and 87 don't have any common factors, so we know we've found our final answer!

Method 2

Method 2 of 2:

Simplifying Complex Fractions Containing Variable Terms

1
When possible, use the inverse multiplication method above. To be clear, virtually any complex fraction can be simplified by reducing its numerator and denominator to single fractions and multiplying the numerator by the inverse of the denominator. Complex fractions containing variables are no exception, though, the more complicated the variable expressions in the complex fraction are, the more difficult and time-consuming it is to use inverse multiplication. For "easy" complex fractions containing variables, inverse multiplication is a good choice, but complex fractions with multiple variable terms in the numerator and denominator may be easier to simplify with the alternate method described below.
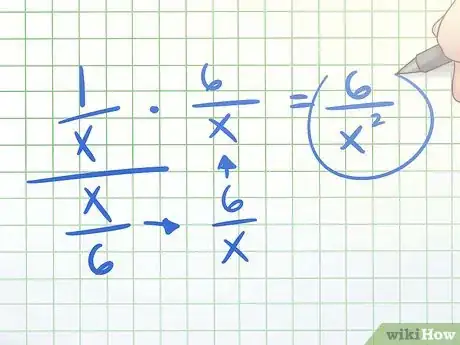
- For example, (1/x)/(x/6) is easy to simplify with inverse multiplication. 1/x × 6/x = 6/x². Here, there is no need to use an alternate method.
- However, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) is more difficult to simplify with inverse multiplication. Reducing the numerator and denominator of this complex fraction to single fractions, inverse multiplying, and reducing the result to simplest terms is likely to be a complicated process. In this case, the alternate method below may be easier.
2
If inverse multiplication is impractical, start by finding the lowest common denominator of the fractional terms in the complex fraction. The first step in this alternate method of simplification is to find the LCD of all the fractional terms in the complex fraction - both in its numerator and in its denominator. Usually, if one or more of the fractional terms have variables in their denominators, their LCD is just the product of their denominators.
- This is easier to understand with an example. Let's try to simplify the complex fraction we mentioned above, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). The fractional terms in this complex fraction are (1)/(x+3) and (1)/(x-5). The common denominator of these two fractions is the product of their denominators: (x+3)(x-5).
3
Multiply the numerator of the complex fraction by the LCD you just found. Next, we'll need to multiply the terms in our complex fraction by the LCD of its fractional terms. In other words, we'll multiply the entire complex fraction by (LCD)/(LCD). We can do this freely because (LCD)/(LCD) is equal to 1. First, multiply the numerator on its own.
- In our example, we would multiply our complex fraction, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), by ((x+3)(x-5))/((x+3)(x-5)). We'll have to multiply through the numerator and denominator of the complex fraction, multiplying each term by (x+3)(x-5).
  - First, let's multiply the numerator: (((1)/(x+3)) + x - 10) × (x+3)(x-5)
    - = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5))
    - = (x-5) + (x(x² - 2x - 15)) - (10(x² - 2x - 15))
    - = (x-5) + (x³ - 2x² - 15x) - (10x² - 20x - 150)
    - = (x-5) + x³ - 12x² + 5x + 150
    - = x³ - 12x² + 6x + 145
4
Multiply the denominator of the complex fraction by the LCD as you did with the numerator. Continue multiplying the complex fraction by the LCD you found by proceeding to the denominator. Multiply through, multiplying every term by the LCD.
- The denominator of our complex fraction, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), is x +4 +((1)/(x-5)). We'll multiply this by the LCD we found, (x+3)(x-5).
  - (x +4 +((1)/(x - 5))) × (x+3)(x-5)
  - = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5).
  - = x(x² - 2x - 15) + 4(x² - 2x - 15) + ((x+3)(x-5))/(x-5)
  - = x³ - 2x² - 15x + 4x² - 8x - 60 + (x+3)
  - = x³ + 2x² - 23x - 60 + (x+3)
  - = x³ + 2x² - 22x - 57
5
Form a new, simplified fraction from the numerator and denominator you just found. After multiplying your fraction by your (LCD)/(LCD) expression and simplifying by combining like terms, you should be left with a simple fraction containing no fractional terms. As you may have noticed, by multiplying through by the LCD of the fractional terms in the original complex fraction, the denominators of these fractions cancel out, leaving variable terms and whole numbers in the numerator and denominator of your answer, but no fractions.
- Using the numerator and denominator we found above, we can construct a fraction that's equal to our initial complex fraction but which contains no fractional terms. The numerator we obtained was x³ - 12x² + 6x + 145 and the denominator was x³ + 2x² - 22x - 57, so our new fraction is (x³ - 12x² + 6x + 145)/(x³ + 2x² - 22x - 57)

Community Q&A

Question

How do I solve 5/6 divided by 1 1/4?

Donagan

Top Answerer

That's 5/6 divided by 5/4, which is solved by multiplying 5/6 by 4/5, which is 20/30 or 2/3.
Question

How do I solve 4/1/4 - 5/2?

Donagan

Top Answerer

4/1/4 is 4 divided by ¼. That's equal to (4)(4) = 16. Then 16 - 5/2 = 16 - 2½ = 13½ or 27/2.
Question

How do I solve 3 2/3 = 2 x/3?

Donagan

Top Answerer

First change the left side to an improper fraction: 3 2/3 = 11/3. Then change the right side to (2x)/3. Now solve for x: 11/3 = 2x/3. Multiply both sides by 3, so that 11 = 2x, and x = 5½.