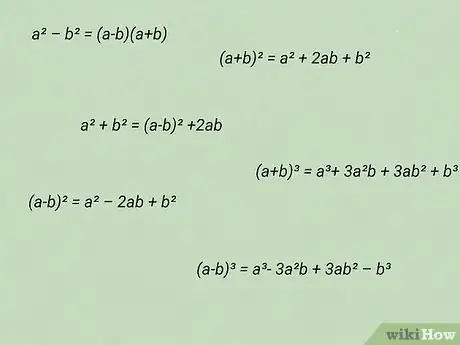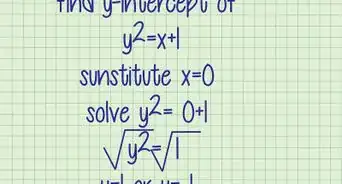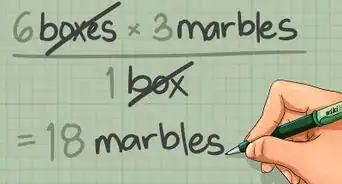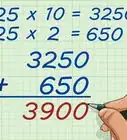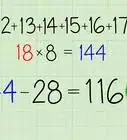How to Solve Math Problems

Although math problems may be solved in different ways, there is a general method of visualizing, approaching and solving math problems that may help you to solve even the most difficult problem. Using these strategies can also help you to improve your math skills overall. Keep reading to learn about some of these math problem solving strategies.

Part 1
Part 1 of 3:

Understanding the Problem

  1. Image titled Solve Math Problems Step 1
    1
    Identify the type of problem. Is it a word problem? Fraction? Quadratic equation? Determine what categorization best fits your math problem before you move forward. Taking the time to identify your problem type is essential to finding the best way to solve the problem.[1]
  2. Image titled Solve Math Problems Step 2
    2
    Read the problem carefully. Even if the problem seems simple, read it very carefully. Don't just skim the problem and attempt to solve it. If the problem is complex, you may need to reread the problem multiple times before you fully understand it. Just take your time and don’t move on until you feel confident that you know what the problem is asking you to do.[2]
    Advertisement
  3. Image titled Solve Math Problems Step 3
    3
    Paraphrase the problem. To help wrap your mind around the problem that you are facing, it may help you to say or write it out into your own words. You can simply say it or write it out if you in a situation where you cannot speak out loud, such as during a test. Check what you have said or written against the original problem to make sure that you are representing the problem accurately. [3] [4]
  4. Image titled Solve Math Problems Step 4
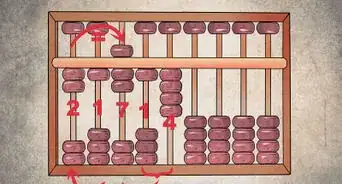
    4
    Draw the problem. If you think it will help with the type of problem you are facing, create a visual representation of the problem to help determine what you need to do next. The drawing does not have to be elaborate, it can simply be a shape or shapes with numbers. Consult the problem as you draw and check your drawing against the problem after you have finished. Ask yourself, “Does my drawing accurately represent the problem?” If it does, then you can move forward. If not, start over by rereading the problem.[5] [6]
    • Draw a Venn diagram. A Venn diagram shows the relationships among the numbers in your problem. Venn diagrams can be especially helpful with word problems. [7]
    • Draw a graph or chart. [8]
    • Arrange the components of the problem on a line. [9]
    • Draw simple shapes to represent more complex features of the problem. [10]
  5. Image titled Solve Math Problems Step 5
    5
    Look for patterns. Sometimes you can identify a pattern or patterns in a math problem simply by reading the problem carefully. You can also create a table to help you identify a pattern or patterns in the problem. Take notes on any patterns that you identify in the problem. These patterns can help you to solve the problem and may even lead you directly to the answer. [11]
  6. Image titled Solve Math Problems Step 6
    6
    Review your information. Check what you have written down against the problem to make sure that you have accurately copied the numbers and other information. Don't go on to the planning stage until you are certain that you have all of the required information and that you fully understand the problem. If you don't understand the problem, take a moment to look at some examples in your textbook or online. Looking at how other people have correctly solved similar problems may help you to understand what this problem is asking you to do.[12]
    7. Advertisement
Part 2
Part 2 of 3:

Developing a Plan

  1. Image titled Solve Math Problems Step 7
    1
    Figure out what formulas you will need to solve the problem. If the problem is particularly complex, you may need more than one. Spend some time reviewing the concepts in your textbook that will help you solve this problem. [13]
  2. Image titled Solve Math Problems Step 8
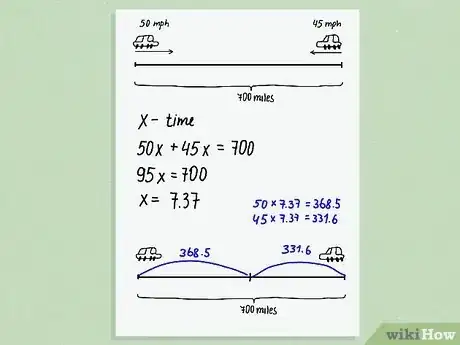
    2
    Write out what you need to do in order to get the answer. Make a step-by-step list of the things that you will need to do to solve the problem. This list will help you to stay organized and focused as you solve the problem. You can also use it to estimate the answer to the problem before you actually solve it. [14] [15]
  3. Image titled Solve Math Problems Step 9
    3
    Work on an easier problem. If there is an easier problem available that is similar to the one you are trying to solve, work on the easier problem first. Solving an easier problem that requires some of the same steps and formulas will help you to tackle the more difficult problem. [16] [17]
  4. Image titled Solve Math Problems Step 10
    4
    Make an educated guess about the answer. Try to estimate the answer before you actually begin to solve it. Identify the numbers and other factors that should contribute to your estimate. Review your estimate and how you made it to determine if you have left anything out. [18] [19]
    5. Advertisement
Part 3
Part 3 of 3:

Solving the Problem

  1. Image titled Solve Math Problems Step 11
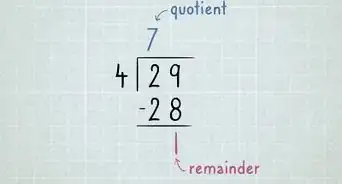
    1
    Follow your plan. Complete the steps that you have identified in the order that you have listed them. Double check each of your answers as you work to ensure accuracy. [20]
  2. Image titled Solve Math Problems Step 12
    2
    Compare your answers to your estimates. As you complete each step, you may also want to compare your answers to the estimates you came up with for each step as well as your overall estimate for the problem’s answer. Ask yourself, “Do my answers match or closely resemble my estimates?” If they do not match up, consider why. Check your answers to see if you have completed all of the steps correctly. [21]
  3. Image titled Solve Math Problems Step 13
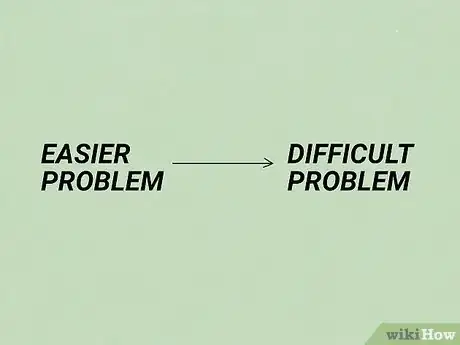
    3
    Try a different plan. If your plan is not working, go back to the planning stage and make a new plan. Don’t be discouraged if this happens, mistakes are common when you are just learning how to do something and you will learn from these mistakes. Accept your mistakes and move on. Try not to dwell on them or get upset. [22]
  4. Image titled Solve Math Problems Step 14
    4
    Reflect on the problem. When you have solved the problem correctly, look back at your process. Taking a moment to reflect on the problem and how you solved it will help you the next time you encounter a similar problem. It will also help you to identify any concepts that you need to learn more about and practice. [23] .
    5. Advertisement

Expert Q&A
Did you know you can get expert answers for this article? Unlock expert answers by supporting wikiHow

  • Question
    How can I make math easier to understand?
    Daron Cam
    Daron Cam
    Academic Tutor
    Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College.
    Daron Cam
    Daron Cam
    Academic Tutor
    Expert Answer

    Support wikiHow by unlocking this expert answer.

    As a student, the vocabulary in math is really important. Aside from regular note-taking, I highly recommend breaking down key terms into its separate components. For example, "trigonometry" is a huge word. If you break it down into its topics on measurement, angle relationships, and right triangles, it becomes a lot easier to understand the subject as a whole.
  • Question
    How can I get better at word problems?
    Daron Cam
    Daron Cam
    Academic Tutor
    Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College.
    Daron Cam
    Daron Cam
    Academic Tutor
    Expert Answer

    Support wikiHow by unlocking this expert answer.

    A lot of times this just comes down to processing what they're asking. So for example, if they're asking a question about an airplane, you could draw a little airplane and jot down each number you're given. Then, ask yourself, "Why are they giving me this information and what can I do with it?" This will often make it easier to transfer that information into an actionable problem.
  • Question
    What is the best way to think about math?
    Community Answer
    Community Answer
    Math is all about finding patterns. Graphs, equations, and data are obvious, but if you look at simple algebra, then you'll find there are patterns there as well. The addition chart, subtraction and division charts, and the infamous times tables, are all filled with intriguing patterns. Although not all math questions need you to find a pattern, it is how Einstein, Stephen Hawking, and many other prominent minds considered mathematics.
Advertisement

You Might Also Like

Do Math Proofs
How to
Do Math Proofs
Do Long Multiplication
How to
Do Long Multiplication
Add 5 Consecutive Numbers Quickly
How to
Add 5 Consecutive Numbers Quickly
Learn Math
How to
Learn Math
Study Math
How to
Study Math
Solve Problems Using Mind Maps
How to
Solve Problems Using Mind Maps
Calculate Percentages
How to
Calculate Percentages
Write Numbers in Words
How to
Write Numbers in Words
Use an Abacus
How to
Use an Abacus
Measure Centimeters
How to
Measure Centimeters
Find the Y Intercept
How to
Find the Y Intercept
Calculate Ratios
How to
Calculate Ratios
Calculate Growth Rate
How to
Calculate Growth Rate
Calculate a Test Grade
How to
Calculate a Test Grade
Advertisement

References

  1. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  2. ↑ Daron Cam. Math Tutor. Expert Interview. 29 May 2020.
  3. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  4. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  5. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  6. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  7. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  8. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  9. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  1. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  2. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  3. ↑ Daron Cam. Math Tutor. Expert Interview. 29 May 2020.
  4. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  5. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  6. ↑ https://math.berkeley.edu/~gmelvin/polya.pdf
  7. ↑ http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
  8. ↑ https://math.berkeley.edu/~gmelvin/polya.pdf
  9. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  10. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  11. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  12. ↑ http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
  13. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf
  14. ↑ http://floridarti.usf.edu/resources/format/pdf/Classroom%20Cognitive%20and%20Metacognitive%20Strategies%20for%20Teachers_Revised_SR_09.08.10.pdf

About This Article

Daron Cam
Co-authored by:
Daron Cam
Academic Tutor
This article was co-authored by Daron Cam. Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary's College. This article has been viewed 551,891 times.
16 votes - 87%
Co-authors: 60
Updated: May 23, 2022
Views: 551,891
Categories: Mathematics
Article SummaryX

To solve a math problem, try rewriting the problem in your own words so it's easier to solve. You can also make a drawing of the problem to help you figure out what it's asking you to do. If you're still completely stuck, try solving a different problem that's similar but easier and then use the same steps to solve the harder problem. Even if you can't figure out how to solve it, try to make an educated guess instead of leaving the question blank. To learn how to come up with a solid plan to use to help you solve a math problem, scroll down!

Did this summary help you?
Advertisement