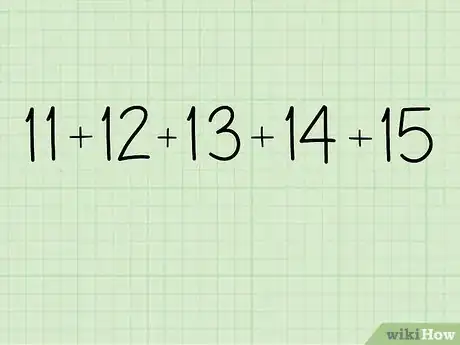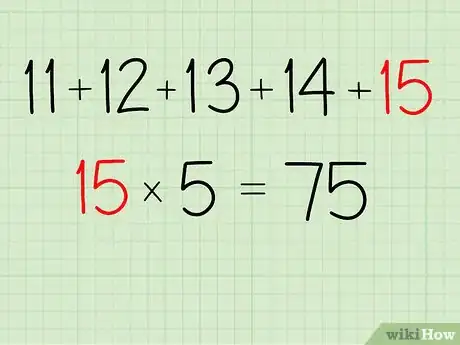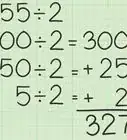This article was co-authored by wikiHow staff writer, Christopher M. Osborne, PhD. Christopher Osborne has been a wikiHow Content Creator since 2015. He is also a historian who holds a PhD from The University of Notre Dame and has taught at universities in and around Pittsburgh, PA. His scholarly publications and presentations focus on his research interests in early American history, but Chris also enjoys the challenges and rewards of writing wikiHow articles on a wide range of subjects.
This article has been viewed 415,973 times.
Learn more...
You might see “162 + 163 + 164 + 165 + 166 = ?” on a math quiz, or hear “Bet you can’t add up the five numbers from 162 through 166” from a friend who likes to boast about their math skills. But guess what — you can do it, and quickly! There are some simple math tricks that make adding up any 5 consecutive numbers easy. You can use them to wow your friends or impress your math teacher!
Steps
Multiplying the Middle Number by 5
-
1Identify the middle number in the series. Let’s say you’re given the numbers 51, 52, 53, 54, and 55. 53 is the middle number in this case, since it has two numbers before and after it in the series.[1]
-
2Multiply the middle number by 5 in your head. This is easier if you’re given small numbers like 1 through 5, of course (since 3 x 5 = 15). But it’s not that much more difficult to mentally multiply 53 x 5 = 265.[2]
- First, separate 53 into 50 and 3.
- Second, multiply 50 x 5 = 250.
- Then, multiply 3 x 5 = 15.
- Finally, add those two results together: 250 + 15 = 265.
Advertisement -
3Confirm that your result ends in 5 or 0. The sum of any 5 consecutive whole numbers will always be divisible by 5, which means it will end in either 5 or 0. So, if your mental math gave you a result of 264 or 266, you know you need to recalculate.[3]
-
4Try it with larger numbers or negative numbers too. For instance, say your consecutive numbers run from 1,263 through 1,267. To mentally multiply the middle number, 1,265, you could add up 5,000 (= 1,000 x 5), 1,000 (= 200 x 5), 300 (= 60 x 5), and 25 (= 5 x 5) to get 6,325 as the sum of 1,263 through 1,267.[4]
- Or, let’s say that your given series is -3, -2, -1, 0, 1. You still multiply the middle number by 5 to get your result — in this case, -1 x 5 = -5, which is also the sum of (-3) + (-2) + (-1) + 0 + 1.
-
5Grab a pencil and paper to see how it works. You can figure out the sum of any series of consecutive whole numbers by using the following formula, in which x = the sum, a = the first number in the series (e.g., 51), and n = the last number in the series (e.g, 55):[5]
- x = (n x ((n + 1) / 2)) - ((a - 1) x (a / 2))
- x = (55 x (56 / 2)) - (50 x 25.5)
- x = (55 x 28) - 1275
- x = 1540 - 1275
- x = 265 (and 265 / 5 = 53, the middle number)
Using the Highest or Lowest Number in the Series
-
1Pick any 5 consecutive numbers. For a simpler example (Example A), try 11, 12, 13, 14, 15.
- For more of a challenge (Example B), try 232, 233, 234, 235, 236.
-
2Multiply the highest number by 5. For Example A, 15 x 5 = 75. For Example B, 236 x 5 = 1,180.
-
3Subtract 10 from your result to get the sum of the series. For Example A, 75 - 10 = 65. For Example B, 1,180 - 10 = 1,170.
-
4Use the lowest number instead by multiplying by 5 and adding 10. For Example A, (11 x 5) + 10 = 55 + 10 = 65. For Example B, (232 x 5) + 10 = 1,160 + 10 = 1,170. As you can see, you end up with the same results.
-
5Compare your result to multiplying the middle number by 5. In Example A, 13 is the middle number, and 13 x 5 = 65. In Example B, 234 is the middle number, and 234 x 5 = 1,170. To do Example B in your head, remember that you can break it up: (200 x 5 = 1,000) + (30 x 5 = 150) + (4 x 5 = 20) = 1,000 + 150 + 20 = 1,170.[6]
-
6Use the formula to further confirm your result. Use x = (n x ((n + 1) / 2)) - ((a - 1) x (a / 2)), where x = the sum, n = the highest number, and a = the lowest number.[7]
- For Example A:
- x = (15 x (16 / 2)) - (10 x 5.5)
- x = (15 x 8) - 55
- x = 120 - 55 = 65
- For Example B:
- x = (236 x (237 / 2)) - (231 x 116)
- x = (236 x 118.5) - 26796
- x = 27966 - 26796 = 1170
- For Example A:
Adding Up Other Amounts of Consecutive Numbers
-
1Add four consecutive numbers by multiplying the highest by 4 and subtracting 6. For example, try 11, 12, 13, 14; 14 x 4 = 56, and 56 - 6 = 50.
- Or, you can multiply the sum of the middle two numbers by two. In the above case, 12 + 13 = 25, and 25 x 2 = 50.[8]
-
2Add six consecutive numbers by multiplying the highest by 6 and subtracting 15. Say you have a consecutive series from 11 through 16. You’d multiply 16 x 6 = 96, then subtract 15 to get 81.
- Alternatively, you can multiply the sum of the middle two numbers by 3. In the above case, 13 + 14 = 27, and 27 x 3 = 81.[9]
-
3Add seven consecutive numbers by multiplying the middle number by 7. If your series runs from 11 through 17, 14 is the middle number. Thus, 14 x 7 = 98.[10]
- For any odd number (3, 5, 7, etc.) of consecutive numbers, you can always just multiply the middle number by the total number in the series.
-
4Add eight consecutive numbers by multiplying the highest by 8 and subtracting 28. If your numbers run from 11 through 18, multiply 18 x 8 = 144, then subtract 144 - 28 = 116.
- You can also multiply the sum of the middle two numbers by 4. In the above example, 14 + 15 = 29, and 29 x 4 = 116.[11]
Community Q&A
-
QuestionWhat are five consecutive whole numbers that add up to 50?
 DonaganTop AnswererLet n be the first number. Then (n) + (n+1) + (n+2) + (n+3) + (n+4) = 50. Combining terms, 5n + 10 = 50. Then 5n = 40, and n = 8. The numbers are 8, 9, 10, 11 and 12.
DonaganTop AnswererLet n be the first number. Then (n) + (n+1) + (n+2) + (n+3) + (n+4) = 50. Combining terms, 5n + 10 = 50. Then 5n = 40, and n = 8. The numbers are 8, 9, 10, 11 and 12. -
QuestionWhat are 5 consecutive whole numbers that equal 15?
 Community AnswerFirst divide 15 by 5 to get the middle number in the sequence. Since there are 5 numbers in the sequence used, we divide by 5. This gives us the number three. We know that this is the middle number in the sequence, so there are an equal amount of numbers both above and below this. Therefore, the numbers must be 1,2,3,4,5. Those five numbers add up to 15 to confirm that this answer is correct.
Community AnswerFirst divide 15 by 5 to get the middle number in the sequence. Since there are 5 numbers in the sequence used, we divide by 5. This gives us the number three. We know that this is the middle number in the sequence, so there are an equal amount of numbers both above and below this. Therefore, the numbers must be 1,2,3,4,5. Those five numbers add up to 15 to confirm that this answer is correct. -
QuestionThe sum of five consecutive numbers is 100. How do I find the first number?
 DonaganTop AnswererLet n be the first number. Then the next four numbers will be n+1, n+2, n+3, and n+4. Add the five numbers together and set them equal to 100: (n) + (n+1) + (n+2) + (n+3) +(n+4) = 100. Add together the five terms on the left to get 5n + 10 and let that equal 100: 5n +10 = 100. Subtract 10 from both sides: 5n = 90. Divide both sides by 5: n = 18. That's the number you're looking for.
DonaganTop AnswererLet n be the first number. Then the next four numbers will be n+1, n+2, n+3, and n+4. Add the five numbers together and set them equal to 100: (n) + (n+1) + (n+2) + (n+3) +(n+4) = 100. Add together the five terms on the left to get 5n + 10 and let that equal 100: 5n +10 = 100. Subtract 10 from both sides: 5n = 90. Divide both sides by 5: n = 18. That's the number you're looking for.
References
- ↑ https://nrich.maths.org/summingconsecutive/solution
- ↑ https://nrich.maths.org/summingconsecutive/solution
- ↑ https://nzmaths.co.nz/resource/consecutive-numbers
- ↑ http://www.math-only-math.com/three-consecutive-numbers.html
- ↑ https://betterexplained.com/articles/techniques-for-adding-the-numbers-1-to-100/
- ↑ http://www.math-only-math.com/three-consecutive-numbers.html
- ↑ https://betterexplained.com/articles/techniques-for-adding-the-numbers-1-to-100/
- ↑ http://www.math-only-math.com/three-consecutive-numbers.html
- ↑ http://www.math-only-math.com/three-consecutive-numbers.html
About This Article
To add 5 consecutive numbers quickly, start by identifying the middle number in the series. For example, if you were trying to add 1, 2, 3, 4, and 5, then 3 would be the middle number. Next, just multiply that number by 5 to get your answer! So in this example, you would multiply 3 by 5 and get 15, which is the same number you'd get if you were to add up 1, 2, 3, 4, and 5. To learn how to add 5 consecutive numbers quickly using the highest and lowest numbers in the series, scroll down!