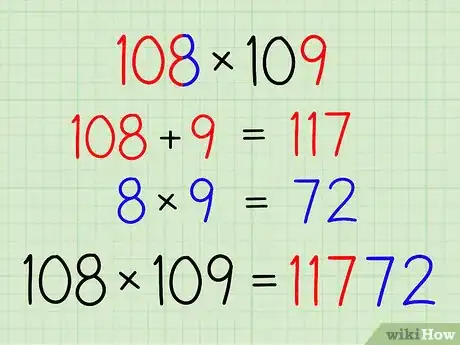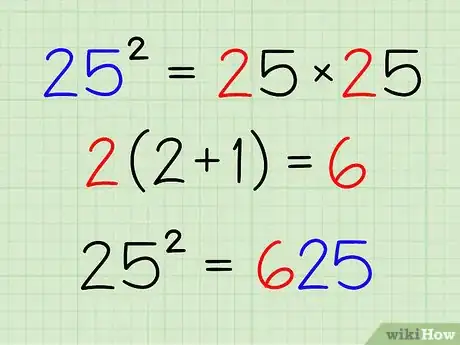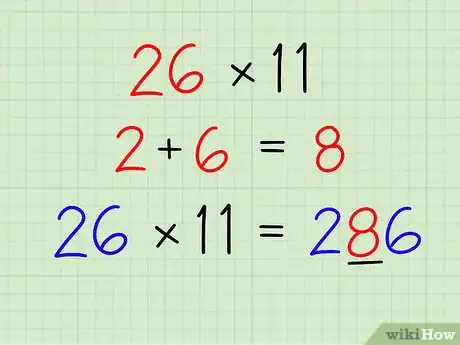How to Speed Up Numeric Calculations in Mathematics

Last Updated: October 23, 2022

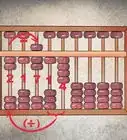
The article shows you some mathematical tricks which will help you to speed up your calculations without using a calculator. The important thing in this approach is recognizing patterns. Once you recognize important patterns, you can develop tricks to apply to certain problems. With some mental calculation practice, you will be able to quickly solve mathematical numeric calculations.

Steps

1
Multiply left to right instead of right to left. Normally we write numbers from left to right, whereas calculations such as multiplication, addition, and subtraction are done from right to left. However, our minds are used to remembering figures from left to right. So for mental multiplication, you can develop a habit of multiplying from left to right.
- Take for instance multiplication of 284*7. Build the answer in three steps.
- First, 2*7=14.
- 14 , 8*7=56 => add 5 to 14 and stick the 6 on the end, i.e 196
- 196, 7*4=28=>add 2 to 196 and stick the 8 on the end, i.e 1988 .
2
Learn this trick to easily calculate the product of numbers just above a base (100,1000,10000).
- Suppose you want to calculate (108*109) where the base is 100. Add 108 and 9 to get 117. Add to the end 9*8, or 72, to get your answer: 11772. Therefore, 108*109=117||72=11772
- Another example: (115*106). Add 115 + 6 = 121, and then stick 90(15*6=90) on the end. 115*106=121||90=12190.
- Another example: 108*113=121||104 =12204. 121 is 113+8, and 104 is 8*13. Add the 1 from 104 to the last digit of 121 to get an answer with the right number of digits, 12204.
- When base is 1000 : Consider 1024*1008. Just write 1032 (1024+8=1032). Suffix it with 192 (024*8=192) to get 1032192.
Advertisement
3
Use this trick to calculate the product of numbers just below a base(100,1000).
- If you want to calculate (98*89) where base is 100, just write 22 [from (100-98=2)*(100-89=11)=22] and prefix it with 87 [from 98-11=87 or 89-2=87].
- When base is 1000: Consider 998*568. Now just write 864 [from (1000-998=2)*(1000-568=432)]. Prefix it with 566 [from 568-2=566 or 998-432=566].
4
Calculate the product of numbers whose first digit is the same and the sum of the last digits is 10.
- Consider the example 32 x 38 = 1216. Both numbers here start with 3 and the last digits (2 and 8) add up to 10.
- Multiply 3 (the first digit of both numbers) by 4 [from (3 + 1)] to get 12 for the first part of the answer.
- And multiply the last figures: 2 x 8 = 16 to get the last part of the answer.
- Similarly:
  - 42*48=20||16=2016
  - 53*57=30||21=3021
  - 99*91=90||09=9009
5
Calculate squares of numbers ending in 5.
- Consider the example 25*25. The last two digits of the answer are 25. The first part of the answer is the product of the first digit of the number being squared and its successor. In this example, the first digit of 25 is 2, and its successor is 3 (2+1=3). 2 * 3 = 6, so the solution is 625.
- Similarly:
  - 35*35=(3*4)||25=1225
  - 45*45=(4*5)||25=2025
  - 95*95=(9*10)||25=9025
6
Use this trick to multiply any number by 11.
- To multiply any 2-figure number by 11 we just put the total of the two digits between the 2 figures. For example, 26 x 11 = 286. Notice that the outer digits in 286 are the 2 and 6 from 26. The middle figure is the sum of 2 and 6.
- 45*11=495
- 65*11=715. This involves a carry: 6+5 = 11, which is now added to the 6 to get 71 for the first two digits.
- For 3 digits, 132*11=1||(1+3=4)||(3+2=5)||2=1452
- 148*11= 1 || (1+4=5 5+1(carry)= 6 ) || (4+8=12 =>2 carry 1)||8 =1628
7
Use this trick to divide a two-digit number by 9:
- 23 / 9 = 2 remainder 5 .The first figure of 23 is 2, and this is the answer. The remainder is just 2 and 3 summed up.
- Similarly:
  - 34/9=3 remainder 7
  - 71/9=7 remainder 8