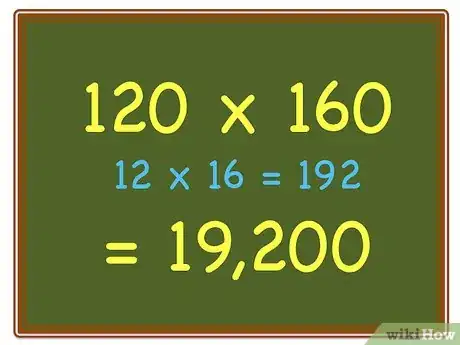How to Teach a Child to Carry Numbers

Last Updated: March 29, 2022

Children are often confused and mystified by the need to carry numbers in addition and multiplication. It's up to you to unveil the secrets and make it simple. Hope you're ready to unleash your inner math teacher!

Method 1

Method 1 of 2:

Addition

1
Have the child learn (and memorize) the basic addition facts.
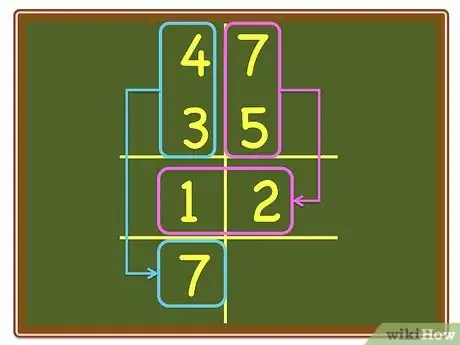
2
Write out a math problem with two digits on the top and bottom. Draw a line between the "units" and the "tens" column to help align and use "place values" in columns. It is not important for your child to already know how to do two column addition.

Advertisement
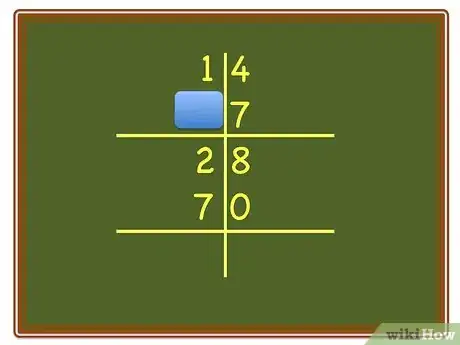
3
Ask the child to answer the units column first, placing both numbers in the correct (lower) positions. Do not have them put a "1" over the numbers, yet.
4
Ask the child to answer the tens column next. Make certain the child places the digit(s) in the correct position (no digit should be in the units column.) If they are confused, cover up the units column. Have the child write the number(s) underneath the number already written in the "tens" column from the "units" column addition.
5
Tell the child that the problem is not finished. Review what you have completed so far.
- If you were using the example above, you might say, "We're almost done. You did seven plus five equals twelve. Good. Four plus three equals seven. Correct. Notice that the four and the three are in the tens position, so you are really adding forty and thirty."
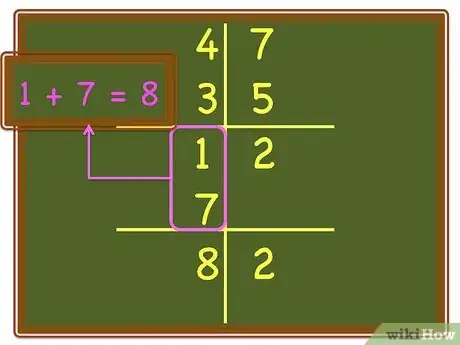
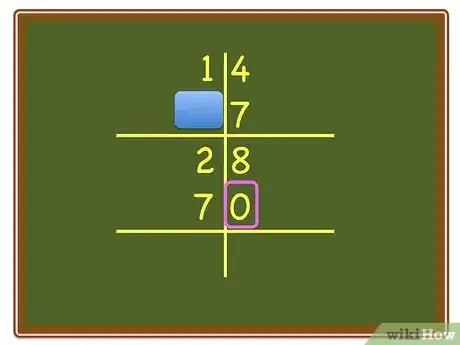
6
Explain that some addition still remains. Have the child bring the amount in the units column down to the bottom. Point to the numbers in the "tens" column and ask the child to add them up.
7
Make certain that the child is comfortable with this before proceeding. By now, the child should already be familiar with the commutative law of addition or (at least) know that the order of addition is unimportant.
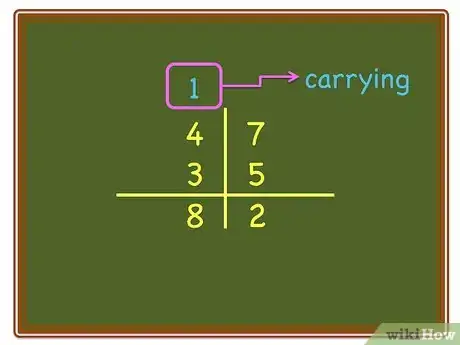
8
Tell the child that, instead of writing the "1" under the tens digit, they are to place the "1" over the "tens" column.
9
Ask the child to add the "1" to the top number of the "tens" column; then add the bottom number to that sum. Tell the child that this is a shortcut we call "carrying", and more commonly called "regrouping" in classrooms today.

Method 2

Method 2 of 2:

Multiplication

This is a more complicated version of the method used in addition. A fringe benefit of this method is that it reveals why estimation works. Before you begin,

1
Make sure the child already knows the basic multiplication tables.
2
Teach the child how to handle multiples of ten; we see this as zeros on the end of a number.
- Simply put: Anytime you multiply by a number with zeros on the end (like 120 x 160), you add the number of zeros to the end of the product.
  120 x 160 becomes:
  12 * 16 = 192
  Place the two zeros on the end (One from 120 and another from 160)
  = 19,200
  Start with a one digit times two digit multiplication problem
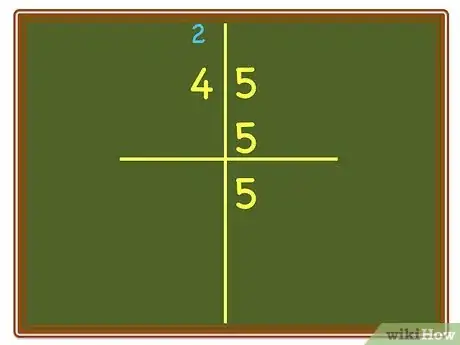
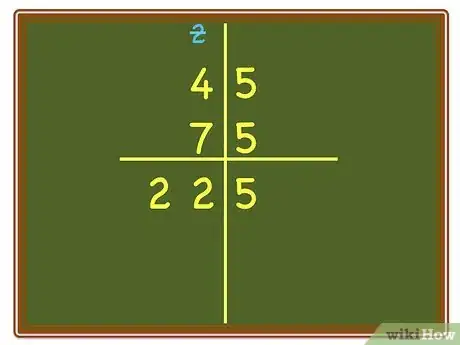
3
Place column lines on the paper and make sure the digits are properly placed.
4
Multiply the Units column and place the answer in the correct columns.
5
Before multiplying the Units column by the Tens column, discuss the implications.
- Remind the child that the units column has already been multiplied. Tell the child that when you multiply the units column by the tens column it's like multiplying something with a zero on the end.
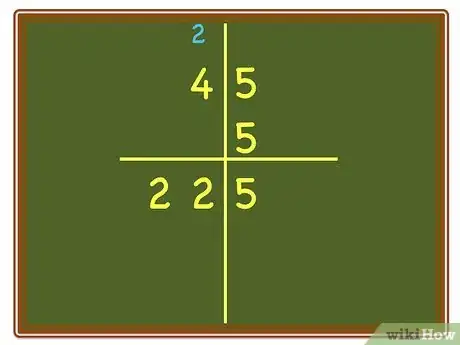
6
Place a zero (0) in the units column underneath the first answer.
7
Multiply the Units column by the tens column and place the answer to the left side of the zero (it will be underneath the first answer).
8
Have the child add the numbers together.
- Do not continue until the child can manage any problem of this type (1 x 2)! Continue with a two digit times two digit (2 by 2) multiplication problem. Most children have no idea why their teacher skips a space on the second line of "conventional" long multiplication.
9
Have the child complete the problem with the bottom tens digit hidden (at first).
10
Remind the child that he/she placed a zero in the right column before multiplying a unit column by a tens column.
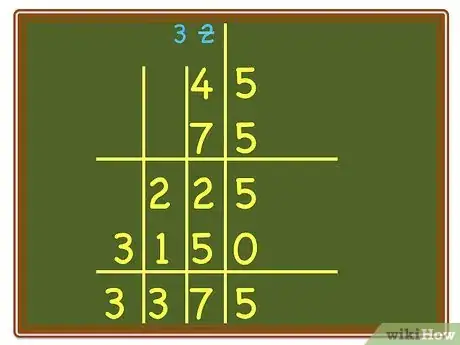
11
Reveal the hidden digit and show the child that he/she will be multiplying a unit by a tens digit again. Mark the two multiplications (which will look like a big X).
12
Again, have the child place a zero(0) in the right hand column and answer the units x tens multiplication to the left of the zero.
13
Discuss multiplying the tens by the tens column. Show the child that this is like multiplying by 100. Have the child place zeros in the two right columns and place the product to the left.
14
Have the child do the addition to finish the problem.
Put it together with unit times two digit (1 by 2) multiplication
15
This time, instead of writing the tens digit (from the unit x unit product) under the line, write it ABOVE the tens digit column.
- Have the child compare this to carrying in addition.
16
Have the child do the units times tens multiplication; have the child add the carried number to the product and write the number to the left of the units digit already present.
- The child should become proficient at this before proceeding.
  Complete the process of (2 by 2) multiplication.
17
Place a tens digit in the lower factor and have the child cross out any carrying that has already taken place.
18
Have the child treat the tens digit like the other one times two digit work. Remind the child of the zero in the right column.
- This would be a good time to tell the child that the zero in the right hand column is not necessary, but it won't hurt if they leave it.
19
Have the child finish by doing the addition.

Community Q&A

Question

What is the answer of doubling 41?

Akitagem

Community Answer

To double 41, you should think of 41+41. Your final answer would be 82.
Question

How do I develop the concept of subtraction in teaching elementary students?

Donagan

Top Answerer

Use a set of physical objects such as blocks. For example, start with five blocks. Take away two blocks. You're left with three blocks.