How to Understand Slope (in Algebra)

Co-authored by wikiHow Staff

Last Updated: January 30, 2023 References Approved

The slope of a line, also called the gradient, measures a line's steepness. We usually think of slope as the “rise over run.” When working with slope it is important to first understand the basic concepts of what slope measures, and how it measures it. You can calculate the slope of a line as long as you know the coordinates of any two points.

Method 1

Method 1 of 3:

Describing the Slope

1
Define slope. The slope is a measure of how steep a straight line is.^{[1]
X
Research source}
- A variety of branches of mathematics use slope. In geometry, you can use the slope to plot points on a line, including lines that define the shape of a polygon. Statisticians use slope to describe the correlation between two variables. Economists use slope to show and predict rates of change.
- People also use slope in real, concrete ways. For example, slope is used when constructing roads, stairs, ramps, and roofs.
2
Visualize a line’s “rise over run.” The term “rise” refers to the vertical distance between two points, or the change in $y$ $y$ . The term “run” refers to the horizontal distance between two points, or the change in $x$ $x$ . When learning about the slope of a line, you will often see the formula ${\text{slope}}\;={\frac {\text{rise}}{\text{run}}}$ ${\text{slope}}\;={\frac {{\text{rise}}}{{\text{run}}}}$ ^{[2]
X
Research source}
- For example a slope of a line might be ${\frac {2}{1}}$ . This means that to go from one point to the next, you need to go up 2 along the y-axis, and over 1 along the x-axis.
Advertisement
3
Locate the slope of a line in an equation. You can do this using the slope-intercept form of a line’s equation. The slope-intercept form says that $y=mx+b$ $y=mx+b$ . In this formula, $m$ $m$ equals the slope of the line. You can rearrange the equation of a line into this formula to find the slope.^{[3]
X
Research source}
- For example, in the equation $y=3x+1$ , the slope would be $3$ . You can still think of this slope in terms of rise over run if you turn it into a fraction. Any whole number can be turned into a fraction by placing it over 1. So, $3={\frac {3}{1}}$ . This means that the line represented by this equation rises 3 units vertically for every 1 unit it runs horizontally.
4
Assess the steepness of the line. The larger the slope, the steeper the line. A line is steeper the more vertical it rests on a coordinate plane.^{[4]
X
Research source}
- For example, a slope of 2 (that is, ${\frac {2}{1}}$ ) is steeper than a slope of 0.5 ( ${\frac {1}{2}}$ ).
5
Identify a positive slope. A positive slope is one that moves up and to the right. In other words, in a positive slope, as $x$ $x$ increases, $y$ $y$ also increases.^{[5]
X
Research source}
- A positive slope is denoted by a positive number.
6
Identify a negative slope. A negative slope is one that moves down and to the right. In other words, in a negative slope, as $x$ $x$ increases, $y$ $y$ decreases.^{[6]
X
Research source}
- A negative slope is denoted by a negative number, or a fraction with a negative numerator.
- To help remember the difference between a positive and negative slope, you can think of yourself as standing on the left endpoint of the line. If you need to walk up the line, it’s positive. If you need to walk down the line, it’s negative.^{[7]
  X
  Research source}
- Knowing the difference between negative and positive slopes can help you check that your calculations are reasonable.
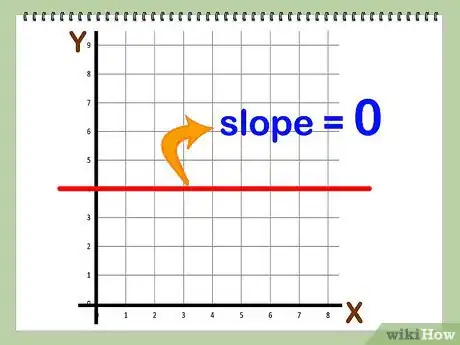
7
Understand the slope of a horizontal line. A horizontal line is a line that runs straight across a coordinate plane. The slope of a horizontal line is 0. This makes sense if you think of lines in terms of ${\text{slope}}\;={\frac {\text{rise}}{\text{run}}}$ . For a horizontal line, the rise is 0, since the $y$ value never increases or decreases. So, the slope of a horizontal line would be ${\frac {0}{x}}$ .
8
Understand the slope of a vertical line. The slope of a vertical line is undefined. In terms of ${\frac {\text{rise}}{\text{run}}}$ , the slope of a negative line would be ${\frac {y}{0}}$ . The run is 0, since the $x$ value never increases or decreases. So, the slope of a vertical line will be ${\frac {y}{0}}$ , and since you can't divide by 0, any number over 0 will always be undefined.^{[8]
X
Research source}

Method 2

Method 2 of 3:

Using a Graph to Find the Slope

1
Set up the formula for the slope of a line. The formula is ${\text{slope}}\;={\frac {\text{rise}}{\text{run}}}$ . The rise is the vertical distance between two points on a line. The run is the horizontal distance between two points on a line.^{[9]
X
Research source}
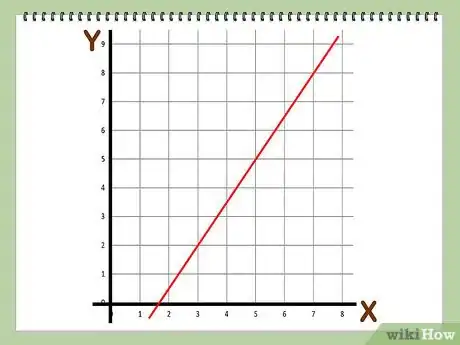
2
Locate two points on the line. You can use two given points, or you can select any two points. It doesn’t matter how far apart or close together the two points are, but keep in mind that if the points are closer together, there will be less need to simplify the slope later.^{[10]
X
Research source}
- For example, you might choose the points (4, 4) and (12, 8).
3
Calculate the vertical distance between the points. Start at one point, and count up in a straight line, until you reach the height of the second point. This is the rise of your slope.^{[11]
X
Research source}
- Your rise will be negative if you start with the higher point and move down to the lower point.
- For example, beginning at the point (4, 4), you would count up 4 positions to point (12, 8). So, the rise of your slope is 4: ${\text{slope}}\;={\frac {4}{\text{run}}}$ .
4
Calculate the horizontal distance between the points. Start at the same point you started at when calculating the run. Count across in a straight line, until you reach the length of the second point. This is the run of your slope.^{[12]
X
Research source}
- Your run will be negative if you start with the point on the right and move over to the left.
- For example, beginning at the point (4, 4), you would count over 8 positions to point (12, 8). So, the run of your slope is 8: ${\text{slope}}\;={\frac {4}{8}}$ .
5
Simplify if necessary. You would simplify the slope just as you would simplify any fraction. ^{[13]
X
Research source}
- For example, 4 and 8 are both divisible by 4, so the slope ${\frac {4}{8}}$ simplifies to ${\frac {1}{2}}$ . Note that it is a positive slope, so the line moves up to the right.

Method 3

Method 3 of 3:

Using Two Points to Find the Slope

1
Set up the formula for the slope of a line. This formula is for finding the slope given two points on a line: $m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ , where $m$ equals the slope of the line, $(x_{1},y_{1})$ equal the coordinates of the starting point on the line, and $(x_{2},y_{2})$ equal the coordinates of the ending point on the line.^{[14]
X
Research source}
2
Plug the x and y coordinates into the formula. To use this method, you need to be given the coordinates, as you will likely not see them plotted on a graph. Don’t forget to keep your coordinates in the correct positions. You should be subtracting the coordinates of the starting point from the coordinates of the ending point.^{[15]
X
Research source}
- For example, if your points are (-4, 7) and (-1, 3), your formula will look like this: $m={\frac {3-7}{-1-(-4)}}$ .
3
Simplify the expression. Subtract the values in the numerator and denominator. Then, simplify the slope, if necessary. You would simplify the slope just as you would simplify any fraction. ^{[16]
X
Research source}
- For example:
  $m={\frac {3-7}{-1-(-4)}}$
  $m={\frac {-4}{3}}$
  So, the slope of the line is ${\frac {-4}{3}}$ . Note that since the slope is negative, the line is moving down to the right.

Community Q&A

Question

What's the slope for y=½x-3?

Donagan

Top Answerer

The slope is 1/2 or 1:2.
Question

How do I find the average rate of change between two points on a slope?

Donagan

Top Answerer

Whether the line is straight or curved, use the slope formula in Method 3 above.