Cómo calcular la amortización

La amortización se refiere a la reducción de una deuda con el transcurrir del tiempo, mediante el pago de una misma suma periódica, por lo general mensual. Con la amortización, el importe a pagar se compone tanto del rembolso del capital como de los intereses sobre la deuda. El capital es el saldo del préstamo que aún está pendiente de pago. Cuanto más capital se rembolse, se deberán menos intereses sobre el saldo. A través del tiempo, la parte de los intereses que se paga mensualmente disminuye y la porción de capital que se rembolsa aumenta. Con frecuencia, la gente se encuentra con la amortización cuando lidia con las hipotecas o con los préstamos automotrices, pero (en términos contables) también puede referirse a la reducción periódica del valor de un activo intangible a lo largo del tiempo.

Parte 1

Parte 1 de 2:
Calcular los intereses y el capital del primer mes

1
Reúne la información necesaria para calcular la amortización del préstamo. Necesitarás el monto del capital y la tasa de interés. Para este propósito, además, necesitarás el plazo del préstamo y el monto de la cuota de cada periodo. En este caso, calcularás la amortización mensual.^{[1]
X
Fuente de investigación}
- El monto del capital es el saldo actual pendiente de pago ($100.000).
- La tasa de interés (6 %) es la tasa anual sobre el préstamo. Para calcular la amortización, convertirás la tasa de interés anual en una tasa mensual.
- El plazo del préstamo es 360 meses (30 años). Ya que en este ejemplo la amortización es un cálculo mensual, el plazo se expresa en meses, no en años.
- La cuota mensual es $599,95. El importe de la cuota se mantiene constante. Sin embargo, los porcentajes de la cuota que corresponden al capital y a los intereses cambiarán.
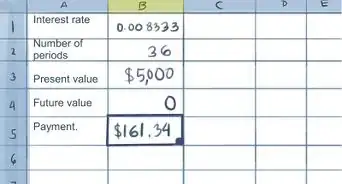
2
Prepara una hoja de cálculo. Este cálculo tiene pocas variables y sería mejor hacerlo en una hoja de cálculo en la que hayas cargado previamente toda la información pertinente en columnas con los siguientes títulos: Capital, Pago de intereses, Pago de capital y Capital final.
- La cantidad total de filas debajo de esos títulos será 360, para contabilizar cada pago mensual.
- Una hoja de cálculo hace los cálculos significativamente más rápido porque, si se hace de la manera correcta, solo tienes que ingresar una ecuación determinada una sola vez (o dos, cuando usas los cálculos del mes anterior para alimentar a todas ecuaciones subsecuentes).
- Una vez que la(s) hayas introducido correctamente, tan solo arrastra hacia abajo la(s) ecuación(es) a través de las demás celdas para calcular la amortización durante el plazo del préstamo.
- Incluso es mejor separar un grupo independiente de columnas e introducir las principales variables del préstamo (por ejemplo, el pago mensual, la tasa de interés, etc.), ya que así podrás visualizar con rapidez cómo los cambios afectan a cada una durante la vida del préstamo.
3
Calcula qué cantidad corresponde a los intereses del primer mes. Para este cálculo se necesitan varios pasos. Tienes que convertir la tasa de interés a una cantidad mensual. La tasa mensual se utiliza para calcular el interés del mes.^{[2]
X
Fuente de investigación}
- Los prestamos que se amortizan, como la hipoteca de una casa o un préstamo automotriz, necesitan un pago mensual. Como resultado, hay que calcular mensualmente las proporciones de cada pago que corresponden a los intereses y al capital, respectivamente.
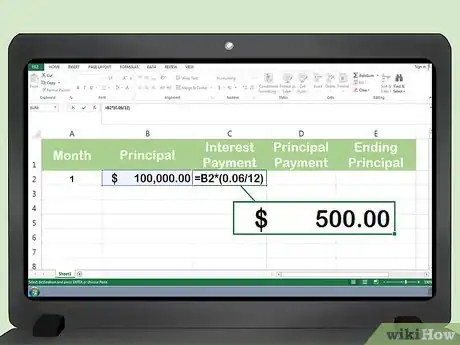
- Convierte la tasa de interés a una tasa mensual. La tasa mensual sería: 6 % / 12 = 0,005 %.
- Multiplica el importe del capital por la tasa de interés mensual: $100.000 X 0,005 % = $500. Este es el interés mensual.
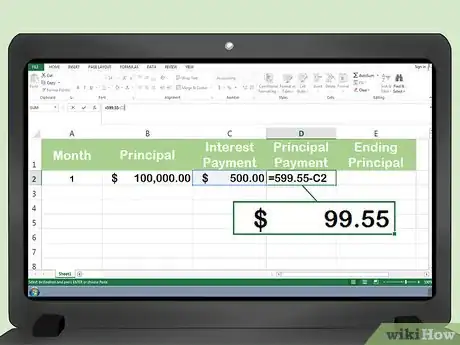
4
Calcula el porcentaje de capital que corresponde al pago del primer mes. Para calcular el importe que corresponde al pago del capital, resta los intereses del pago mensual.^{[3]
X
Fuente de investigación}
- Resta los intereses mensuales del pago mensual para calcular el pago del capital: $599,55 - $500 = $99,55. Ese es el pago del capital.
- Cuanto más capital se rembolse, los intereses que debas sobre el saldo principal disminuirán. Un porcentaje mayor de cada pago mensual se asignará al rembolso del capital.
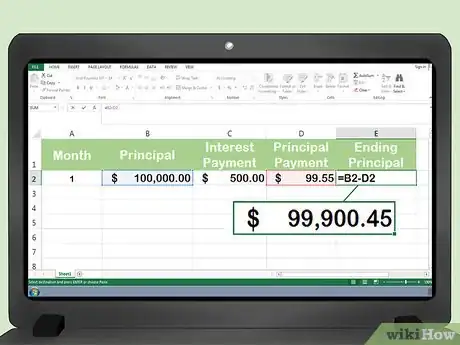
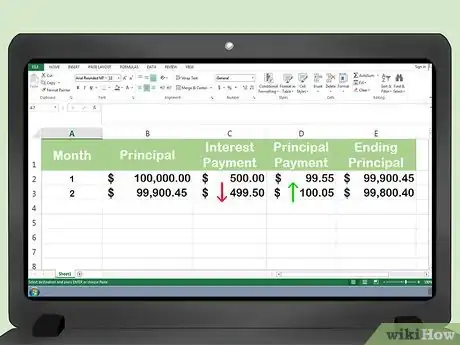
5
Utiliza el nuevo importe del capital al final del primer mes para calcular la amortización del segundo mes. Cada vez que calcules la amortización, restarás el monto del capital rembolsado el mes anterior.^{[4]
X
Fuente de investigación}
- Calcula el monto del capital para el segundo mes: $100.000 - $99,55 = $99.900,45.
- Calcula los intereses para el segundo mes: $99.900,45 X 0,005 % = $499,50.
6
Establece el rembolso del capital para el segundo mes. Tal como lo hiciste el primer mes, el interés mensual se resta del pago mensual total del préstamo. La cantidad restante es el rembolso de capital correspondiente a ese mes.^{[5]
X
Fuente de investigación}
- Calcula el rembolso del capital en el segundo mes: $599,55 - $499,50 = $100,05.
- El rembolso de capital en el segundo mes ($100,05) es mayor que el del primer mes ($99,55). Ya que el saldo total del capital disminuye cada mes, se pagan menos intereses sobre el saldo. En el primer mes fueron $500. En el segundo mes, los intereses solo son $499,50.
- Como el pago exigido de intereses disminuye, el porcentaje del pago que va al capital se incrementa.

Parte 2

Parte 2 de 2:
Calcular la amortización para todo el plazo del préstamo

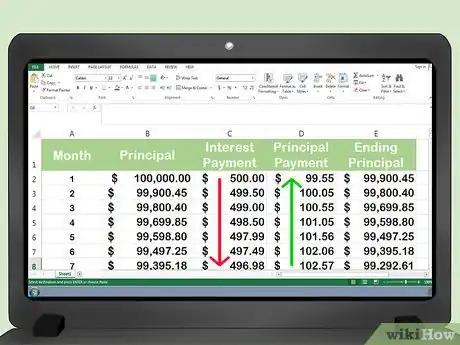
1
Analiza la tendencia que se da en el tiempo. Puedes ver que el capital del préstamo disminuye cada mes. Ya que el monto del capital disminuye, los intereses que se calculan sobre un monto menor de capital también disminuyen. A lo largo del tiempo, una cantidad creciente de cada pago mensual irá al capital.^{[6]
X
Fuente de investigación}
- Calcula el nuevo saldo de capital para el tercer mes: $99.900,45 - $100,05 = $99.800,40.
- Calcula los intereses del tercer mes: $99.800,40 X 0,005 % = $499.
- Calcula el pago del capital en el tercer mes: $599,55 - $499 = $100,55.
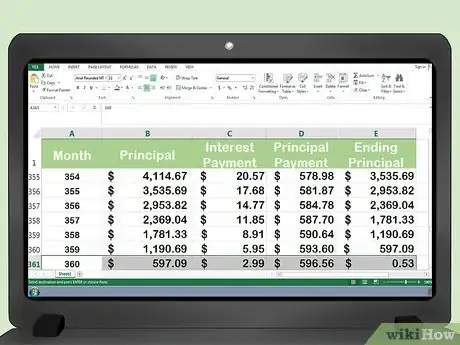
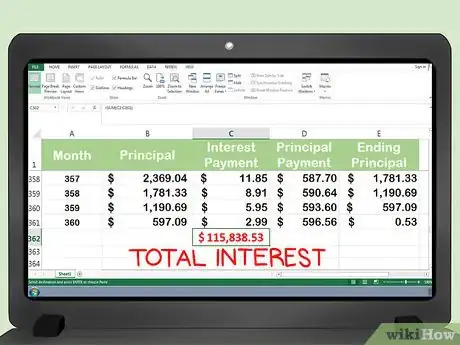
2
Ten en cuenta el impacto de la amortización al final del plazo del préstamo. Verás que, a lo largo del tiempo, el importe de los intereses que se cargan cada mes disminuye. El porcentaje de capital en cada pago se incrementa progresivamente.^{[7]
X
Fuente de investigación}
- El pago de intereses disminuye a casi cero. En el último mes del plazo del préstamo, el pago de intereses equivale a $2,98.
- El ultimo periodo del plazo, el porcentaje del pago que corresponde al capital ($596,37) está cerca del importe total del pago.
- Al finalizar el plazo, el importe de capital adeudado es $0.
3
Utiliza el concepto de amortización para decidir inteligentemente respecto a tus finanzas. Ya que el préstamo hipotecario y el préstamo automotriz usan la amortización, tienes que entender este concepto. Puedes utilizar tus conocimientos sobre amortización para gestionar tus deudas personales.^{[8]
X
Fuente de investigación}
- Siempre que puedas, haz pagos adicionales para reducir más rápido el monto del capital. Cuanto más rápido reduzcas el monto del capital, menos intereses pagarás durante el plazo del préstamo.
- Evalúa la tasa de interés sobre las deudas que tengas pendientes de pago. Los pagos adicionales tendrán un mayor impacto sobre los préstamos que tengan la tasa de interés más alta. Debes reducir el importe del capital de la deuda que tenga la tasa de interés más alta.
- En Internet puedes encontrar calculadoras de amortización de préstamos. Emplea una de ellas para calcular el interés que ahorrarías al hacer pagos adicionales. Digamos, por ejemplo, que con el pago adicional reduces el monto del capital de $10.000 a $9.900.
- Utiliza los $10.000 para calcular la amortización durante el plazo remanente del préstamo. Cambia el capital de $10.000 a $9.900 y haz los cálculos nuevamente. Fíjate en el total de intereses pagados durante el plazo del préstamo. Verás una diferencia con base en el pago adicional de capital de $100.