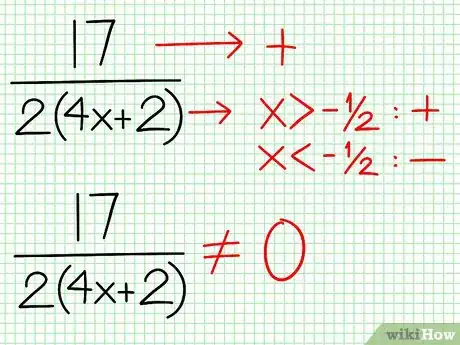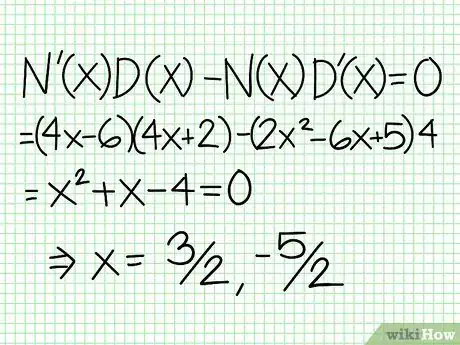Cómo graficar una función racional

Información del autor

Una función racional es una ecuación que tiene la forma y = N(x)/D(x), donde N y D son polinomios. Tratar de dibujar una gráfica exacta de una de ellas a mano conlleva un exhaustivo repaso de muchos de los temas más importantes de la preparatoria desde álgebra básica hasta cálculo diferencial. Considera el siguiente ejemplo: y = (2x² - 6x + 5)/(4x + 2).

Pasos

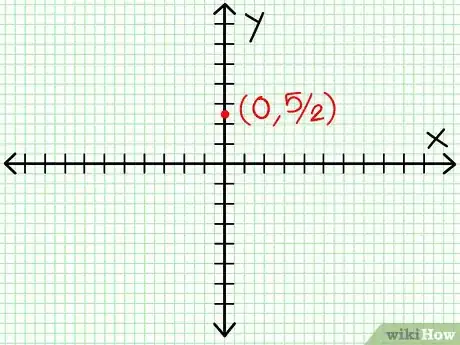
1
Encuentra la intersección con y." Sólo iguala x = 0. Todo excepto los términos constantes desaparecen, dejando y = 5/2. Al expresar esto como un par coordenado, (0, 5/2) es un punto en la gráfica.
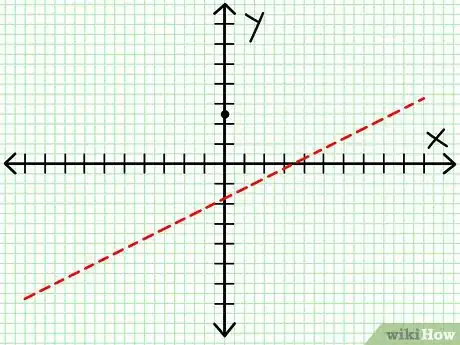
2
Encuentra la asíntota horizontal. Divide el denominador entre el numerador para determinar el comportamiento de y para valores mayores y absolutos de x. En este ejemplo, la división muestra que y = (1/2)x - (7/4) + 17/(8x + 4). Para valores grandes positivos o negativos de x, 17/(8x + 4) se acerca a cero y la gráfica se aproxima a la línea y = (1/2)x - (7/4). Usando una línea punteada o muy delgada, se grafica la siguiente línea.
- Si el grado del numerador es menor que el grado del denominador, no se puede dividir, y la asíntota queda como y = 0.
- Si deg(N) = deg(D), la asíntota es una línea horizontal del cociente de los coeficientes principales.
- Si deg(N) = deg(D) + 1, la asíntota es una línea, cuya pendiente es el cociente de los coeficientes principales.
- Si deg(N) > deg(D) + 1, entonces para valores grandes de |x|, y va rápidamente al infinito positivo o negativo como una cuadrática, cúbica o de un grado polinomial mayor. En este caso, es probable que no valga la pena graficar con exactitud el cociente de la división.
3
Encuentra los ceros. Una función racional tiene un cero cuando su numerador es cero, así que iguala N(x) = 0. En el ejemplo, 2x² - 6x + 5 = 0. El discriminante de esta cuadrática es b² - 4ac = 6² - 4*2*5 = 36 - 40 = -4. Dado que el discriminante es negativo, N(x), y consecuentemente f(x), no tiene raíces reales. La gráfica nunca cruza el eje x. Si se llega a encontrar algún cero, se deben agregar esos puntos a la gráfica.
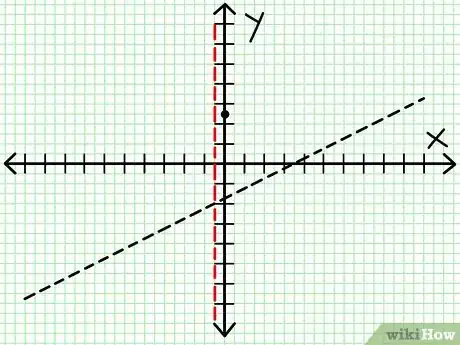
4
Encuentra las asíntotas verticales. Una asíntota vertical ocurre cuando el denominador es cero. Al igualar 4x + 2 = 0 te da la línea vertical x = -1/2. Grafica cada asíntota vertical con una línea muy delgada o punteada. Si algún valor de x hace tanto N(x) = 0 como D(x) = 0, puede que haya o no asíntotas verticales ahí. Esto es raro, pero ve los consejos de qué hacer si esto llegara a pasar.
5
Verifica el residuo de la división en el paso 2. ¿Cuándo es positivo, negativo o cero? En el ejemplo, el numerador del residuo es 17, que es siempre positivo. El denominador, 4x + 2, es positivo a la derecha de la asíntota vertical y negativo a la izquierda. Esto significa que la gráfica se acerca a la asíntota lineal por arriba para valores grandes positivos de x y por abajo para valores negativos grandes de x. Ya que 17/(8x + 4) nunca puede ser cero, esta gráfica nunca intersecta la línea y = (1/2)x - (7/4). No agregues nada a la gráfica por ahora, pero toma en cuenta estas conclusiones para más tarde.
6
Encuentra los extremos locales. Un extremo local puede ocurrir siempre que N'(x)D(x)- N(x)D'(x) = 0. En el ejemplo, N'(x) = 4x - 6 y D'(x) = 4. N'(x)D(x) - N(x)D'(x) = (4x - 6)(4x + 2) - (2x² - 6x + 5)*4 = 0. Al expandirlo, agrupar términos y dividir entre 4, queda como resultado: x² + x - 4 = 0. La fórmula cuadrática tiene raíz cerca de x = 3/2 and x = -5/2. (Estos difieren aproximadamente por 0.06 del valor exacto, pero nuestra gráfica no será lo suficientemente precisa como para preocuparnos por esa clase de detalles. Al escoger una aproximación racional decente, el siguiente paso será más sencillo.)
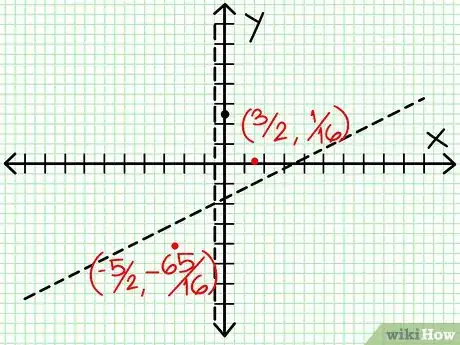
7
Encuentra el valor de y para cada extremo local. Evalúa los valores de x del paso anterior de nuevo en la función racional original para encontrar el valor correspondiente de y. En el ejemplo, f(3/2) = 1/16 y f(-5/2) = -65/16. Añade estos puntos, (3/2, 1/16) y (-5/2, -65/16), a la gráfica. Debido a que usamos valores aproximados en el paso anterior, estos no serán los máximos y mínimos exactos, pero están muy cercanos a ellos. (Sabemos que (3/2, 1/16) es muy cercano al valor mínimo local. Del paso 3, sabemos que y es positiva siempre que x > -1/2 y encontramos un valor tan pequeño como 1/16, así que al menos en este caso, el error es probablemente menor que el espesor de la línea.)
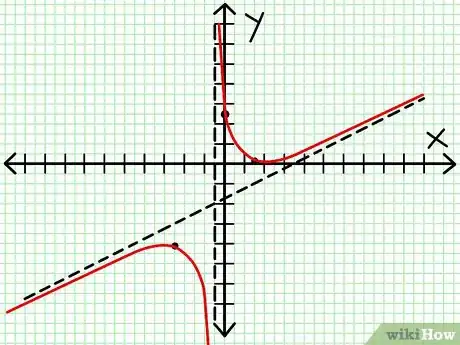
8
Conecta los puntos y extiende la gráfica con cuidado a través de los puntos conocidos hacia las asíntotas, cuidando de realizar su aproximación desde la dirección correcta. Ten cuidado de no cruzar el eje x excepto en los puntos encontrados en el paso 3. No intersectes la asíntota horizontal o lineal, excepto en los puntos que se encontraron en el paso 5. No cambies de una pendiente creciente a una decreciente, excepto en los puntos extremos encontrados en el paso anterior.

Consejos

En casos raros, el numerador y el denominador pueden tener un factor común que no sea constante. Si estás siguiendo los pasos, esto se mostrará como un cero y una asíntota vertical en el mismo lugar. Dado que esto es imposible, lo que realmente sucede es uno de los siguientes casos:
- El cero en el N(x) tiene una multiplicidad mayor que el cero en D(x). La gráfica de f(x) se aproxima a cero en este punto, pero es indefinida ahí. Esto se indica con un círculo sin relleno alrededor del punto.
- El cero en el N(x) y el cero en D(x) tienen la misma multiplicidad. La gráfica se aproxima a algún punto diferente de cero para este valor de x, pero es indefinida ahí. De nuevo, esto se indica con un círculo abierto.
- El cero en el N(x) tiene una multiplicidad menor que el cero en D(x). Aquí hay una asíntota vertical.
Algunos de estos pasos pueden involucrar la resolución de un polinomio de grado mayor. Si no puedes encontrar soluciones exactas a través de factorización, fórmulas u otros medios, entonces estima la solución utilizando técnicas numéricas tales como el método de Newton.
Si sigues estos pasos en orden, usualmente no será necesario usar también pruebas derivativas de segundo grado o métodos similares potencialmente complicados para determinar si los valores críticos son máximos locales, mínimos locales, o ninguno de los anteriores. Trata de usar información de los pasos anteriores y un poco de lógica primero.
Si estás tratando de hacer esto sólo con métodos de precálculo, puedes reemplazar los pasos sobre encontrar los extremos locales mediante la computación de muchos pares ordenados adicionales (x, y) entre cada par de asíntotas. Alternativamente, si no te importe cómo sucede, no hay razón por la cual un estudiante de precálculo no pueda tomar la derivada de un polinomio y resolver N'(x)D(x) - N(x)D'(x) = 0.