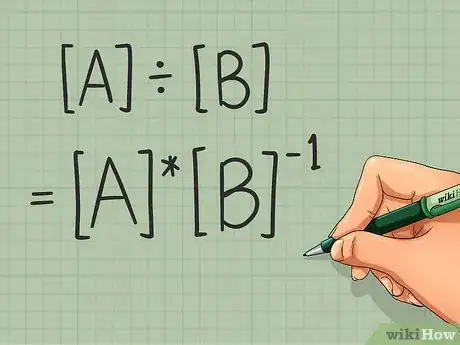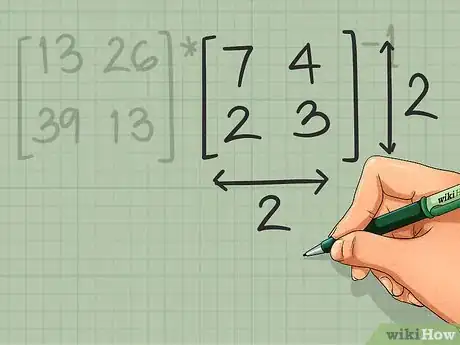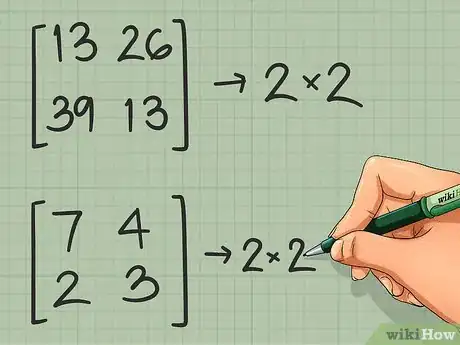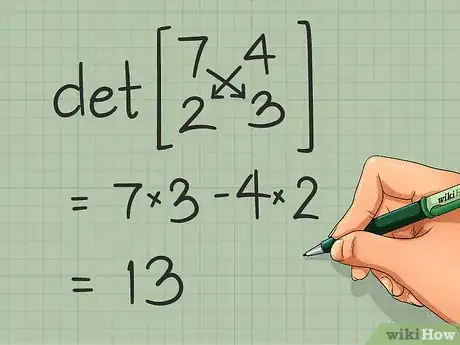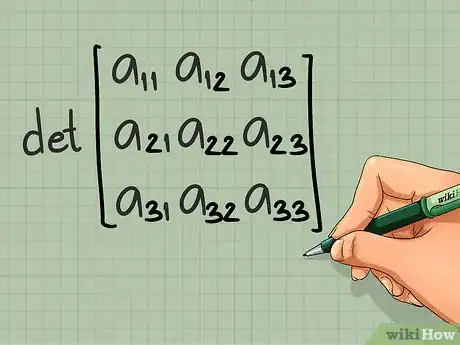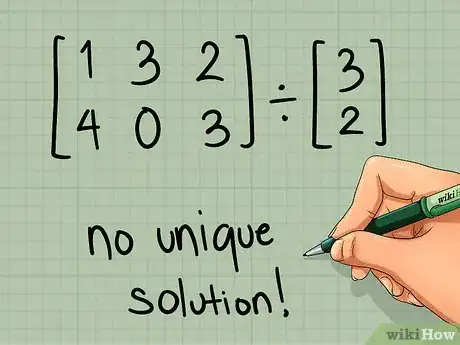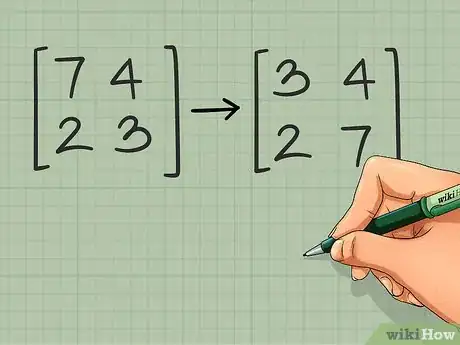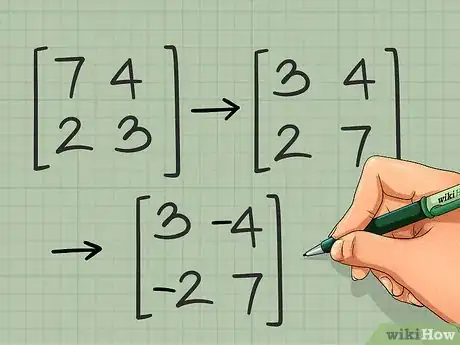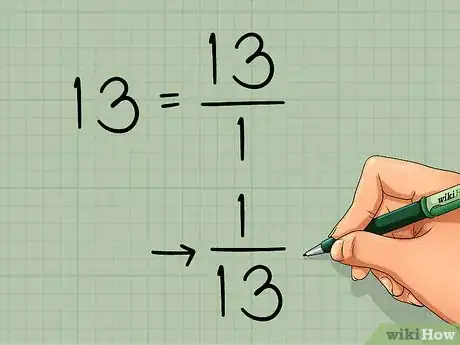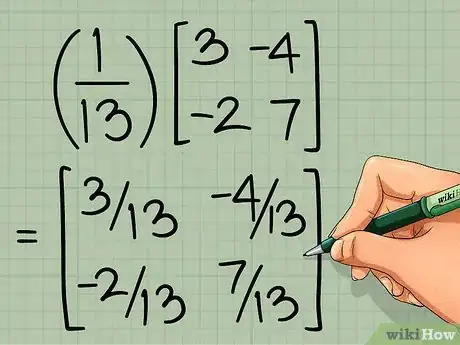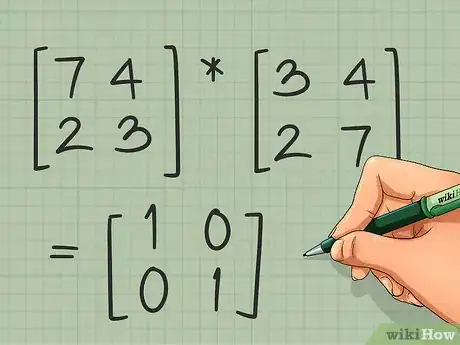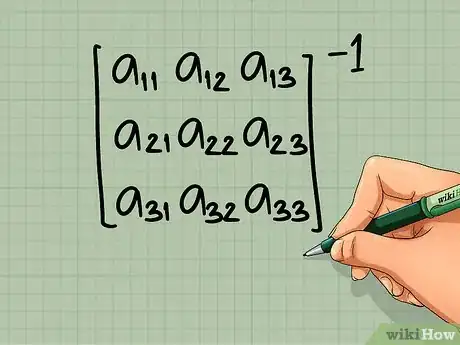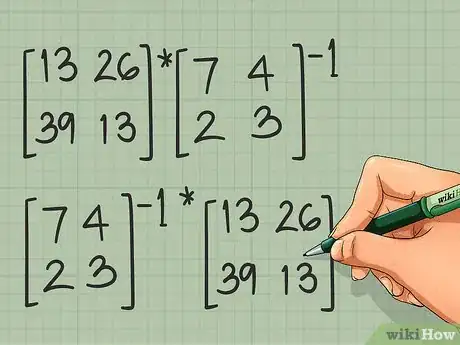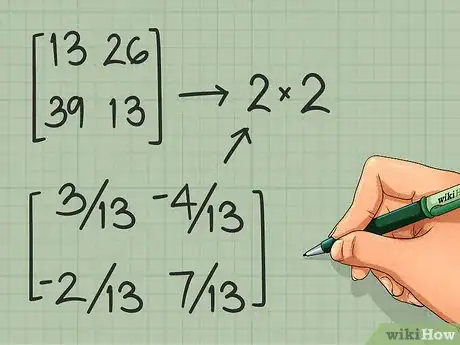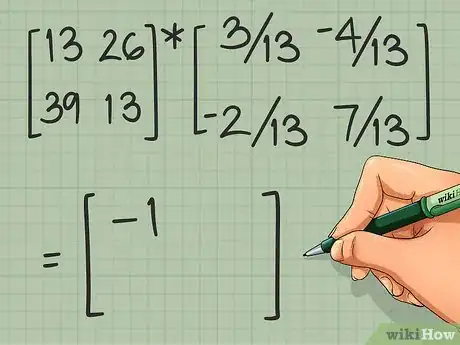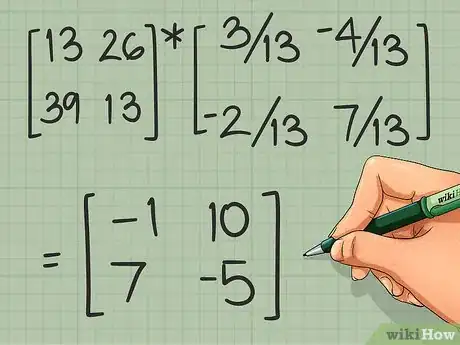Comment diviser des matrices

Si vous savez multiplier deux matrices entre elles, alors vous devriez être capable de diviser l'une par l'autre. En fait, la division est un raccourci de langage : il s'agit plutôt de multiplier une matrice par l'inverse de l'autre. Si l'on devait comparer avec la division entre entiers, c'est comme si l'on vous demandait de diviser 10 par 5, vous devriez alors multiplier 10 par l'inverse de 5 (soit 5^-1, c'est-à-dire ¹/₅). L'opération est alors : 10 x 5^-1, et vous devriez trouver le même résultat qu'en faisant directement la division. La division des deux matrices étant un non-sens mathématique, multiplier par l'inverse d'une matrice reste ce qui se rapproche le plus d'une division, sans en être une au sens mathématique du terme. Cette opération est fréquemment utilisée pour résoudre des systèmes d'équations linéaires ^{[1]
X
Source de recherche}.

Partie 1

Partie 1 sur 3:

Savoir si la division d’une matrice est possible

1
Comprenez bien ce qu'est la « division » d'une matrice par une autre. En fait, c'est une opération qui n'existe pas en tant que telle : elle n'a aucun sens, les mathématiciens n'utilisent même pas le terme ^{[2]
X
Source de recherche}. L'opération qui s'en approche le plus est la multiplication d'une matrice par l'inverse de l'autre. Autrement dit, vous ne verrez jamais l'opération [A] ÷ [B], car c'est un non-sens mathématique. Par contre, vous pourrez calculer [A] x [B]^-1. Si ces deux opérations sont équivalentes pour des quantités scalaires (nombres), il convient d'utiliser la seconde si vous avez à « diviser » des matrices.
- L'ordre a aussi son importance : le produit [A] x [B]^-1 n'est pas égal à [B]^-1 x [A]. Pour vous en convaincre, faites les deux opérations et vous verrez que les solutions diffèrent.
- Ainsi, au lieu d'écrire ${\begin{pmatrix}13&26\\39&13\end{pmatrix}}\div {\begin{pmatrix}7&4\\2&3\end{pmatrix}}$ , écrivez ${\begin{pmatrix}13&26\\39&13\end{pmatrix}}\times {\begin{pmatrix}7&4\\2&3\end{pmatrix}}^{-1}$ .
  Posez également l'opération suivante : ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}^{-1}\times {\begin{pmatrix}13&26\\39&13\end{pmatrix}}$ , laquelle à une réponse différente de la première.
2
Vérifiez que la matrice diviseuse est carrée. L'inverse d'une matrice n'existe que pour les matrices carrées, c'est-à-dire ayant le même nombre de rangées et de colonnes. Si ce n’était pas le cas, il y aurait plusieurs solutions à votre problème ^{[3]
X
Source de recherche}.
- Le terme « diviseuse » est totalement inapproprié, car il ne s’agit en aucune façon d’une division au sens où on l’entend habituellement. Dans l'opération [A] x [B]^-1, la matrice de division est la matrice [B]. Pour revenir à notre exemple, c'est la matrice ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}$ .
- Une matrice ayant un inverse est dite « inversible » ou « régulière », celle qui n'en a pas est dite « singulière ».
3
Voyez si les deux matrices peuvent être multipliées. Pour cela, vérifiez que le nombre de colonnes de la première matrice est le même que celui des rangées de la seconde ^{[4]
X
Source de recherche}. Si cela ne se vérifie ni pour [A] x [B]^-1 ni pour [B]^-1 x [A], c’est que l’opération n’est pas possible.
- Ainsi, si [A] est une matrice 4 x 3 et [B], une matrice 2 x 2, votre problème n’a pas de solution. Le produit [A] x [B]^-1 ne peut pas se faire, car 4 ≠ 2, non plus que le produit [B]^-1 x [A], puisque 2 ≠ 3.
- Observez que la matrice inverse [B]^-1 a le même nombre de colonnes et de lignes que la matrice de départ [B]. Pour l'instant, il n'est pas nécessaire de la calculer.
- Dans l'exemple choisi, les deux matrices sont de type 2 x 2, elles peuvent donc être multipliées simplement.
4
Calculez le déterminant de la matrice de division. En effet, avant de trouver la matrice inverse, vous devez calculer le déterminant de cette matrice, lequel doit être non nul, sans quoi vous n'aurez pas d'inverse : c'est une condition sine qua non. Le calcul d'un déterminant est somme toute simple.
- Pour une matrice 2 x 2, comme c'est le cas pour la matrice ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ , le déterminant est : ad - bc ^{[5]
  X
  Source de recherche}. Vous faites le produit de la diagonale qui part du haut à gauche et va en bas à droite, produit auquel vous retranchez le produit de l'autre diagonale.
- Ainsi, la matrice ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}$ a pour déterminant : (7)(3) - (4)(2) = 21 - 8 = 13. Comme il est non nul, il est possible d'établir la matrice inverse.
5
Trouvez le déterminant d'une plus grande matrice. Si vous avez affaire à une matrice 3 x 3 ou plus grande encore, le calcul du déterminant est juste un peu plus long.
- Pour une matrice 3 x 3: prenez en considération n'importe quel élément de la matrice et retirez mentalement la ligne et la colonne sur lesquelles se trouve cet élément : vous obtenez une matrice 2 x 2. Calculez-en le déterminant selon la méthode précédente. Faites de même avec un deuxième élément pris sur la même colonne (ou ligne), vous avez un deuxième déterminant. Enfin, prenez en considération le troisième élément de la colonne (ou ligne), et vous obtenez un troisième déterminant. Pour finir, additionnez les trois déterminants. Consultez cet article pour devenir un as des déterminants de matrices.
- Pour le calcul de matrices plus grandes, utilisez une calculatrice graphique ou un logiciel de calcul. La méthode est la même que pour la matrice 3 x 3, mais vous comprenez bien que les calculs deviennent, à défaut d'être compliqués, plus nombreux : le travail devient vite fastidieux ^{[6]
  X
  Source de recherche}. Pour vous donner une idée du travail à faire, trouver le déterminant d'une matrice 4 x 4, consiste à trouver les déterminants de quatre matrices 3 x 3.
6
Faites à présent le point. Si votre matrice n'est pas carrée ou si le déterminant est nul, votre exercice s'arrête là, car il n'admet pas de solution unique. Si votre matrice est carrée et si son déterminant est non nul, alors vous pouvez passer à l'étape suivante : la détermination de la matrice inverse.

Publicité

Partie 2

Partie 2 sur 3:

Trouver l’inverse d’une matrice

1
Intervertissez deux éléments de la diagonale principale. Avec une matrice 2 x 2, il existe une astuce qui permet d'aller plus vite ^{[7]
X
Source de recherche}. Elle consiste à intervertir dans un premier temps l'élément situé en haut à gauche avec celui situé en bas à droite.
- Reprenons l'exemple : ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}$ devient ${\begin{pmatrix}3&4\\2&7\end{pmatrix}}$ .
- Nota bene : Pour les matrices 3 x 3 ou plus grandes, les étudiants se servent de leur calculatrice scientifique, mais cela peut aussi se faire à la main, voyez plutôt à la fin de cette partie.
2
Prenez l'inverse des deux autres éléments. Ils ne bougent pas de position, l'opération consiste donc à multiplier l'élément en haut à droite et l'élément en bas à gauche par -1.
- ${\begin{pmatrix}3&4\\2&7\end{pmatrix}}$ → ${\begin{pmatrix}3&-4\\-2&7\end{pmatrix}}$
3
Trouvez l'inverse du déterminant. Dans la partie précédente, vous avez trouvé le déterminant de la matrice, il va nous servir à présent. Inscrivez l’inverse de ce nombre sous la forme : ${\frac {1}{d{\acute {e}}terminant}}$ ${\frac {1}{d{\acute e}terminant}}$ .
- Dans notre exemple, le déterminant est 13. Son inverse est donc : ${\frac {1}{13}}$ .
4
Multipliez cette nouvelle matrice par l'inverse du déterminant. Multipliez chaque élément de la matrice par l'inverse que vous venez de trouver. La matrice ainsi obtenue est l’inverse de la matrice 2 x 2.
- ${\frac {1}{13}}\times {\begin{pmatrix}3&-4\\-2&7\end{pmatrix}}$
  = ${\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}$
5
Vérifiez vos calculs. Pour cela, multipliez la matrice originale par la matrice de départ. Si vos calculs sont justes, vous devriez trouver la matrice identité, soit ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ . Si c'est ce que vous constatez, vous pouvez passer au paragraphe suivant.
- Reprenons notre exemple. Multipliez ${\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}\times {\begin{pmatrix}7&4\\2&3\end{pmatrix}}={\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ .
- Pour vous rafraichir la mémoire sur la multiplication des matrices, lisez cet article.
- Nota bene : la multiplication n'est pas commutative, ce qui signifie que l'ordre des opérants a son importance. Par contre, quand vous multipliez une matrice par son inverse, l'ordre importe peu, le résultat sera le même : la matrice identité ^{[8]
  X
  Source de recherche}.
6
Révisez la façon de calculer l'inverse d'une matrice 3 x 3. Cet article vaut aussi pour les matrices plus grandes. À moins que vous n'ayez envie de comprendre comment elles se calculent, il est beaucoup plus simple et plus rapide d'utiliser une calculatrice graphique (ou un logiciel dédié) pour les grandes matrices. Si vous devez faire les calculs, voyez ci-dessous une des méthodes possibles ^{[9]
X
Source de recherche} ^{[10]
X
Source de recherche}.
- Accolez la matrice identité (I) à la droite de votre matrice. Ainsi, [B] → [B | I ]. La matrice identité ne présente que des « 1 » sur la diagonale principale et des « 0 » sur l'autre.
- Lancez une série de réductions linéaires en divisant chaque élément à la même place dans les deux moitiés par le même chiffre. Continuez ainsi jusqu'à ce que la moitié de gauche soit la matrice identité.
- Une fois les réductions faites, votre matrice est la suivante : [I | B^-1], I étant la matrice identité. La moitié droite de la matrice étendue est cette fois la matrice inverse (celle que vous cherchez) de la matrice de départ.
Publicité

Partie 3

Partie 3 sur 3:

Multiplier des matrices pour les diviser

1
Inscrivez les deux équations possibles. En calcul algébrique classique, la multiplication est commutative. C'est ainsi que : 2 x 6 = 6 x 2. Par contre, elle ne l'est pas entre matrices, ce qui implique que vous avez deux problèmes à résoudre.
- Dans l'équation x[B] = [A], la matrice x vaut [A] x [B]^-1.
- Dans l'équation [B]x = [A], la matrice x vaut [B]^-1 x [A].
- Si dans un problème d'équations linéaires, vous devez, par exemple, résoudre [A] = [C], et que vous soyez obligé de multiplier chaque membre par [B]^-1, [B]^-1[A] ne sera pas égal à [C][B]^-1, parce que [B]^-1 est à gauche de [A] et que, dans l'autre membre, elle est à droite à droite de [C]. Vous devez respecter l'ordre ^{[11]
  X
  Source de recherche}.
2
Déterminez les dimensions de la matrice produit. Celles-ci sont les dimensions extérieures des deux matrices, ce qui veut dire que la matrice produit a autant de lignes que la première matrice et autant de colonnes que la seconde matrice.
- Revenons à notre exemple de départ. Nous avions les matrices ${\begin{pmatrix}13&26\\39&13\end{pmatrix}}$ et ${\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}$ qui, toutes deux, sont des matrices 2 x 2, la réponse sera alors une matrice 2 x 2.
- Il n'en va pas de même si, par exemple, la matrice [A] est une matrice 4 x 3 et [B]^-1, une matrice 3 x 3. Le produit [A] x [B]^-1 donnera une matrice 4 x 3.
3
Trouvez la valeur du premier élément. Pour cela, lisez ou relisez cet article ou lisez le petit mémento qui suit pour vous rafraichir la mémoire.
- Pour trouver l'élément de la première ligne et de la première colonne de la matrice [A][B]^-1, vous devez calculer le produit scalaire de la ligne 1 de la matrice [A] par la colonne 1 de la matrice [B]^-1, ce qui pour une matrice 2 x 2 donne : $(a_{1,1}\times b_{1,1})+(a_{1,2}\times b_{2,1})$ .
- Dans notre exemple ${\begin{pmatrix}13&26\\39&13\end{pmatrix}}\times {\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}$ , l'élément de la première ligne et de la première colonne sera :
  $(13\times {\frac {3}{13}})+(26\times {\frac {-2}{13}})$
  $=(3)+(-4)$
  $=-1$
4
Calculez tous les produits scalaires pour chacun des éléments. Ainsi, l'élément situé en position (2,1) est le produit scalaire de la ligne 2 de la matrice [A] par la colonne 1 de la matrice [B]^-1. Essayez de faire seul les calculs suivants, vous devriez trouver les matrices suivantes :
- ${\begin{pmatrix}13&26\\39&13\end{pmatrix}}\times {\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}={\begin{pmatrix}-1&10\\7&-5\end{pmatrix}}$
- Si vous devez calculer l'autre solution, elle est la suivante : ${\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}\times {\begin{pmatrix}13&26\\39&13\end{pmatrix}}={\begin{pmatrix}-9&2\\19&3\end{pmatrix}}$
Publicité

Conseils

Il est possible de diviser une matrice par un scalaire : divisez chaque élément par ce scalaire.
- Ainsi, si vous devez diviser la matrice ${\begin{pmatrix}6&8\\2&4\end{pmatrix}}$ par 2, vous obtiendriez : ${\begin{pmatrix}3&4\\1&2\end{pmatrix}}$ .

Avertissements

Une calculatrice ne peut faire que ce pour quoi elle est programmée, ce qui fait qu'elle n'est pas toujours cohérente concernant le calcul matriciel. Ainsi, si vous voyez s'afficher à l'écran une réponse du type « 2e^-8 », vous pouvez être certain que l'élément est en fait 0 ^{[12]
X
Source de recherche}.