حول توازن السطوح

حول توازن السطوح (بالإغريقية: Περὶ ἐπιπέδων ἱσορροπιῶν)‏ هي أطروحة ألفها أرخميدس في مجلدين. احتوي الكتاب الأول على برهان لقانون الرافعة وتوج ببراهين حول مركز ثقل المثلث وشبه المنحرف.[1][2] الكتاب الثاني، احتوي على عشرة براهين، تدور حول مراكز ثقل القطع المستقيمة المكافئية.[1]

حول توازن السطوح
(بالإغريقية: Περὶ ἐπιπέδων ἱσορροπιῶν)‏ 
معلومات الكتاب
المؤلف أرخميدس 
اللغة اليونانية الدوريكية
تاريخ النشر القرن 3 ق.م 
النوع الأدبي مقالة 
الموضوع مركز ثقالة  ‏،  ورافعة 

وفقًا لبابوس الإسكندري، فإن عمل أرخميدس على الرافعات جعله يقول: "أعطني مكانًا أقف عليه، وسأحرك الكرة الأرضية" (بالإغريقية: δός μοί ποῦ στῶ καὶ κινῶ τὴν γῆν)‏، ولكن هناك حالة من الغموض حول سياق المقولة في المصادر القديمة الأخرى.[3][4]

ملخص

لم يكن أرخميدس أول من حلل مبدأ عمل الرافعة، فقد كانت الرافعة وخصائصها معروفة جيدًا قبل عصره.[5] احتوى كتاب المسائل الميكانيكية المنسوب لأرسطو، على برهان فضفاض لقانون الرافعة لا يستخدم مفهوم مركز الثِقَل. هناك عمل قصير آخر منسوب لإقليدس بعنوان "حول الاتزان" On the Balance يحتوي أيضًا على برهان رياضي لقانون الرافعة، أيضا لا يستخدم مركز الثقل.[6]

في المقابل، فإن مفهوم مركز الثقل يحتل الصدارة في كتاب أرخميدس.[7] ففي الكتاب الأول، المحتوي على سبع مسلمات وخمسة عشر برهانا، استخدم مركز الثقل لكل من الكميات المتقايسة وغير المتقايسة لبرهنة قانون الرافعة، وبرغم ذلك يرى البعض بأن البرهان غير مُرضٍ.[2] ثم يشرع أرخميدس في تحديد مركز ثقل متوازي الأضلاع والمثلث، وينهي الكتاب الأول بإثبات بمركز ثقل شبه المنحرف.

يشترك الكتاب الثاني في نفس موضوع الكتاب الأول ولكن كُتِبَ في تاريخ لاحق. ويحتوي على عشرة براهين مرتبطة حصريًا بمركز ثقل القطع المستقيمة المكافئية، وفحص هذه القطع المستقيمة باستبدالها بمستطيلات مساوية لها في المساحة. هذا الاستبدال أصبح في الإمكان بعد نشر أطروحة تربيع القطع المكافئ، المُعتَقد أنها نُشرت بعد الكتاب الأول.[1][2]

المحتويات

الكتاب الأول

يتناول النصف الأول من الكتاب الأول خصائص الاتزان وقانون الرافعة، بينما يركز النصف الثاني على مركز ثقل أشكال المستوى الأساسية. يستخدم القانون على وجه الخصوص الفرضية الأولى، التي تنص على أن "الأوزان المتساوية على مسافات متساوية تكون في حالة توازن". في البرهانين 4 و 5، يتوسع أرخميدس في استخدام هذه الفرضية بإثبات أن مركز ثقل أي نظام من عدد زوجي من الأوزان المتساوية، الموزعة بالتساوي، سيكون موجودًا في منتصف المسافة بين مركزي الثقل. ثم يستخدم أرخميدس هذه النظريات لإثبات قانون الرافعة في البرهان 6 (للحالات المتقايسة) والبرهان 7 (للحالات غير المتقايسة).

البرهان
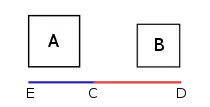
الأوزان والروافع عند نسبة أربعة إلى ثلاثة.

لو لدينا وزنين غير متكافئين، ولكن متقايسين، وكانت ذراع الرافعة مقسمة لجزأين غير متساويين، لكن متقايسين (انظر الرسم) ، لو وضعنا الكميتين A و B عند النقطتين E و D، على التوالي، فسيكون النظام في حالة توازن إذا كانت الأوزان تتناسب عكسياً مع الأطوال:

لنفترض أن المسافات والأوزان مختارة طبقا لقاعدة التناسب باستخدام مقياس مشترك (أو وحدة) لنسمها N، وبنسبة أربعة إلى ثلاثة. الآن، نضاعف طول ED بتكرار الذراع الأطول على اليسار والذراع الأقصر على اليمين.

لغرض التوضيح، أعد ترتيب الخطوط بحيث يصبح CD مجاورًا لـ LE (الخطان الأحمران معًا)، ومقابلين للترتيب الأصلي (على النحو التالي):

من الواضح أن كلا الخطين ضعف الخط الأصلي ED، وأن مركز LH يقع عند E، وأن مركز HK يقع عند D. لاحظ بالإضافة لذلك أن EH (المساوي لـ CD) يكافيء عدد محدد من المرات من الوحدة المشتركة N، كذلك EC، وبالتبعية أيضا CH. يبقى إذن إثبات أن A الموجود عند E، وB الموجود عند D، لهما مركز ثقل عند C.

لذا ولأن نسبة LH إلى HK قد ضاعفت المسافات الأصلية CD و EC، بالمثل نقسّم المقدارين A و B لنسبة ثمانية لستة (وهو تحويل يحافظ على النسبة الأصلية أربعة لثلاثة)، وبمحاذاتهم بحيث تتركز وحدات A (الحمراء) عند E، بينما تتركز وحدات B (الزرقاء) عند D.

الآن، ولأن عددًا زوجيًا من الأوزان المتساوية متباعدة عن بعضها بشكل متساوٍ، ومركز ثقلها في المنتصف، فإن الثقل A يوجد في الواقع عند E (في منتصف LH)، وB عند D (في منتصف HK)، كما يتطلب البرهان. وإضافة لهذا نرى أن النظام الكلي يحتوي على عدد زوجي من الأوزان المتساوية الموزعة بالتساوي، لذا وطبقا لنفس القانون، يكون C مركز الثقل للنظام بأكمله. ولذا فإن النظام في حالة توازن.[1]

الكتاب الثاني

موضوع الكتاب الثاني الرئيسي هو تحديد مركز ثقل أي جزء من قطعة مكافئية، كما أظهر البرهان 8.

بدأ الكتاب بإثبات بسيط لقانون الرافعة في البرهان 1،مستخدما النتائج المنشورة في تربيع القطع المكافئ. قدم أرخميدس بعد ذلك سبعة براهين مستخدما مركز الثقل وخصائص القطع المكافئ التي عرضها في الكتاب الأول. النتيجة الأهم التي توصل لها أن قطعين مكافئين متساويين في المساحة يقع مركز ثقلهما على نفس المسافة من نقطة معينة، ثم لاحقا يستبدل مساحتيهما بمستطيلات لهم نفس المساحة الكلية.[1]

البرهانان الأخيران، 9 و10، لحد ما بهما شيء من الصعوبة ولكنهما يركزان على تحديد مركز ثقل شكل نتج من قطع جذع لقطعة مستقيمة مكافئية.[8]

أثر العمل

كانت كتابات أرخميدس الميكانيكية، بما في ذلك حول توازن السطوح، معروفة ولكن قليلة القراءة في العصور القديمة. اقتبس كلا من هيرو وببس من أرخميدس على نطاق واسع في مؤلفاتهم على الميكانيكا، غالبا فيما يخص مركز الثقل والفائدة الميكانيكية. ويبدو أن بعض المؤلفين الرومان، مثل فيتروفيوس، كان لديهم بعض المعرفة بكتابه أيضًا.[9][10]

في العصور الوسطى، كان بعض المؤلفين العرب على دراية بكتاب أرخميدس وأضافوا إلى نتائجه في الموازين ومراكز الثقل. في الغرب اللاتيني، كانت هذه الأفكار غائبة تقريبًا عدا حالات محدودة.[11][12] فقط في عصر النهضة، انتشرت على نطاق واسع نتائح من كتاب حول توازن الأسطح. وبالخصوص أصبح تعامل أرخميدس الرياضي مع الفيزياء، نموذجًا للعلماء اللاحقين مثل كويدوبالدو ديل مونتي، وبرناردينو بالدي [الإنجليزية]، وسيمون ستيفين، وجاليليو جاليلي.[13][14]

تطور مفهوم مركز الثقل بشكل كبير جدًا في النصف الثاني من القرن السابع عشر، ولا سيما في أعمال إيفانجليستا تورشيللي وكريستيان هوغنس، ولعب دورًا محوريًا في تطوير الميكانيكا العقلانية mécanique rationelle.[15][16]

نقد

سلط عدد من الأبحاث الضوء على التناقضات في الكتاب الأول من كتاب حول توازن السطوح.[2] شكك بيرجرين Berggren في صحة الكثير من الكتاب الأول، مشيرًا كمثال للاطناب في البراهين 1-3 و11-12. ومع ذلك، اتَّبَع إدوارد جان دايكسترهاوس [الإنجليزية] في رفض نقد ماخ للبرهان 6 وأبرز أهميته بدلاً من ذلك، تحديدا "إذا كان نظام الأوزان المعلق على عارضة التوازن في حالة إتزان عند تعليقه عند نقطة معينة، فإن أي إعادة توزيع للأوزان تراعي مركز ثقلهم المشترك، لن تغير من حالة التوازن تلك".[2][8]

يبدو أن البرهان 7 من الكتاب الأول غير مكتمل في شكله الحالي، لأن أرخميدس وضح قانون الرافعة للأوزان المتقايسة فقط.[17][18] يخلو الكتاب الثاني من هذه المشاكل لأنه، باستثناء البرهان الأول، لا يتناول الرافعة على الإطلاق.[19] ربما كان غياب تعريف لمركز الثقل في أي مكان من أعمال أرخميدس الموجودة أمرا مثيرا للقلق، لأنه يُصَعِّب فهم البنى المنطقية لبعض حججه في أطروحته حول توازن السطوح.[20][21]

مراجع
  1. Heath, T.L. (1897)، "The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)"، Cambridge University Press.، مؤرشف من الأصل في 06 أكتوبر 2007، اطلع عليه بتاريخ 06 يناير 2013.
  2. Berggren, J. L. (1976)، "Spurious Theorems in Archimedes' Equilibrium of Planes Book I"، Archive for History of Exact Sciences 16(2), 87-103، ISSN 1432-0657.
  3. Quoted by ببس الرومي in Synagoge, Book VIII, p. 1060 in ed. Hultsch
  4. Berryman, S. (2020)، "How Archimedes Proposed to Move the Earth"، Isis، 111 (3): 562–567، doi:10.1086/710317، ISSN 0021-1753، مؤرشف من الأصل في 8 يوليو 2022.
  5. Goe, G. (1972)، "Archimedes' theory of the lever and Mach's critique"، Studies in History and Philosophy of Science Part A (باللغة الإنجليزية)، 2 (4): 329–345، doi:10.1016/0039-3681(72)90002-7، ISSN 0039-3681، مؤرشف من الأصل في 5 نوفمبر 2021.
  6. Renn, J., Damerow, P., & McLaughlin, P. (2003). Aristotle, Archimedes, Euclid, and the origin of mechanics: The perspective of historical epistemology. In J. L. Montesinos Sirera (Ed.), Symposium Arquímedes Fundación Canaria Orotava de Historia de la Ciencia (pp. 43–59). http://www.mpiwg-berlin.mpg.de/Preprints/P239.PDF.
  7. Magnaghi, C. P.؛ Assis, A. K. T. (07 مايو 2012)، "Calculation of the centre of gravity of the cone utilizing the method of Archimedes"، European Journal of Physics، 33 (3): 637–646، doi:10.1088/0143-0807/33/3/637، ISSN 0143-0807، مؤرشف من الأصل في 8 يوليو 2022.
  8. Dijksterhuis, E.J. (1987)، Archimedes، Princeton University Press, Princeton، ISBN 0-691-08421-1. Republished translation of the 1938 study of Archimedes and his works by an historian of science.
  9. Drachmann, A. G. (1968)، "Archimedes and the Science of Physics"، Centaurus (باللغة الإنجليزية)، 12 (1): 1–11، doi:10.1111/j.1600-0498.1968.tb00074.x، ISSN 0008-8994، مؤرشف من الأصل في 12 مارس 2022.
  10. Assis (2010)، Archimedes, the Center of Gravity, and the First Law of Mechanics (ط. 2nd)، C. Roy Keys Incorporated، ISBN 9780986492648.
  11. Clagett, M. (1959)، "The Impact of Archimedes on Medieval Science"، Isis، 50 (4): 419–429، ISSN 0021-1753، مؤرشف من الأصل في 12 يوليو 2022.
  12. Høyrup, J. (2019)، Høyrup (المحرر)، "Archimedes – Knowledge and Lore from Latin Antiquity to the Outgoing European Renaissance"، Selected Essays on Pre- and Early Modern Mathematical Practice (باللغة الإنجليزية)، Cham: Springer International Publishing، : 459–477، doi:10.1007/978-3-030-19258-7_17، ISBN 978-3-030-19258-7، مؤرشف من الأصل في 12 يوليو 2022
  13. Palmieri, P. (2008)، "Breaking the circle: the emergence of Archimedean mechanics in the late Renaissance"، Archive for History of Exact Sciences (باللغة الإنجليزية)، 62 (3): 301–346، doi:10.1007/s00407-007-0012-8، ISSN 1432-0657، مؤرشف من الأصل في 16 يونيو 2018.
  14. Meli (2010)، "The axiomatic tradition in seventeenth-century mechanics"، Discourse on a New Method: Reinvigorating the Marriage of History and Philosophy of Science (باللغة الإنجليزية)، ص. 23–41، ISBN 978-0-8126-9662-2، مؤرشف من الأصل في 5 يناير 2016.
  15. Pisano, R.؛ Bussotti, P.؛ Bussotti, Paolo؛ Bussotti, Paolo (2014)، "Notes on mechanics and mathematics in Torricelli as physics mathematics relationships in the history of science."، Problems of Education in the 21st Century، 61: Discontinuous، doi:10.33225/pec/14.61.88، ISSN 1822-7864، مؤرشف من الأصل في 30 يوليو 2021.
  16. Van Dyck, M. (2020)، "Mechanical philosophy : science of mechanics"، Encyclopedia of early modern philosophy and the sciences، Springer، : 1–11، ISBN 978-3-319-20791-9، مؤرشف من الأصل في 12 يوليو 2022
  17. Heath, T.L. (1897)، "The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)"، Cambridge University Press.، مؤرشف من الأصل في 06 أكتوبر 2007، اطلع عليه بتاريخ 06 يناير 2013.Heath, T.L. (1897). "The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)". Cambridge University Press. Archived from the original on 6 October 2007. Retrieved 2013-01-06.
  18. Berggren, J. L. (1976)، "Spurious Theorems in Archimedes' Equilibrium of Planes Book I"، Archive for History of Exact Sciences 16(2), 87-103، ISSN 1432-0657.Berggren, J. L. (1976). "Spurious Theorems in Archimedes' Equilibrium of Planes Book I". Archive for History of Exact Sciences (Internet). Archive for History of Exact Sciences 16(2), 87-103. ISSN 1432-0657.
  19. Dijksterhuis, E.J. (1987)، Archimedes، Princeton University Press, Princeton، ISBN 0-691-08421-1.Dijksterhuis, E.J. (1987). Archimedes. Princeton University Press, Princeton. ISBN 0-691-08421-1. Republished translation of the 1938 study of Archimedes and his works by an historian of science.
  20. Goe, G. (1972)، "Archimedes' theory of the lever and Mach's critique"، Studies in History and Philosophy of Science Part A (باللغة الإنجليزية)، 2 (4): 329–345، doi:10.1016/0039-3681(72)90002-7، ISSN 0039-3681.Goe, G. (1972). "Archimedes' theory of the lever and Mach's critique". Studies in History and Philosophy of Science Part A. 2 (4): 329–345. doi:10.1016/0039-3681(72)90002-7. ISSN 0039-3681.
  21. Magnaghi, C. P.؛ Assis, A. K. T. (07 مايو 2012)، "Calculation of the centre of gravity of the cone utilizing the method of Archimedes"، European Journal of Physics، 33 (3): 637–646، doi:10.1088/0143-0807/33/3/637، ISSN 0143-0807.Magnaghi, C. P.; Assis, A. K. T. (2012-05-07). "Calculation of the centre of gravity of the cone utilizing the method of Archimedes". European Journal of Physics. 33 (3): 637–646. doi:10.1088/0143-0807/33/3/637. ISSN 0143-0807.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.