مبرهنة المثلث القائم لفيرما
مبرهنة المثلث القائم لفيرما هي إثبات على عدم الوجود في نظرية الأعداد ، نُشرت عام 1670 بين أعمال بيير دي فيرما ، بعد وفاته بفترة وجيزة. هذا هو الإثبات الكامل والوحيد الذي قدمه فيرما. [1] لدى المبرهة العديد من الصيغ المكافئة ، تم ذكر إحداها (بدون إثبات) عام 1225 بواسطة فيبوناتشي . تنص في أشكالها الهندسية على:
- لا يمكن أن تكون للمثلث القائم في المستوى الإقليدي الذي تكون أطوال أضلاعه الثلاثة أعدادًا كسرية مساحة تساوي مربع عدد نسبي (كسري).
- لا يمكن لمثلث قائم الزاوية ومربع بمساحات متساوية أن تتقايس جميع الأضلاع مع بعضها البعض.
- لا يوجد مثلثين قائمين حيث يكون ضلع أحد المثلثين هو الساق والوتر للمثلث الآخر.
بشكل أكثر تجريدًا ، كنتيجة حول المعادلات الديوفانتية (عدد صحيح أو حلول عدد نسبي للمعادلات متعددة الحدود) ، فإن المبرهنة تكافئ العبارات الآتية:
- إذا كانت ثلاثة أعداد مربعة تشكل متتالية حسابية، فإن الفجوة بين الأعداد المتتالية في المتتالية (تسمى التطابق ) لا يمكن أن تكون مربع بحد ذاتها.
- النقاط الكسرية الوحيدة على المنحنى الإهليلجي هي ثلاث نقاط بديهية مع و .
- المعادلة الرباعية ليس لها حل في الأعداد الصحيحة غير الصفرية.
الصياغة
المربعات في المتتاليات الحسابية
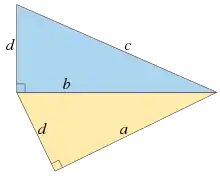
في عام 1225 ، تحدى الإمبراطور فريدريك الثاني عالم الرياضيات فيبوناتشي للمشاركة في مسابقة رياضية ضد العديد من علماء الرياضيات الآخرين ، مع ثلاث مشاكل وضعها فيلسوف بلاطه جون باليرمو. طلبت أول هذه المسائل ثلاثة أعداد كسرية بحيث مربعاتها متباعدة بشكل متساوٍ بمقدار خمس وحدات ، وحلها فيبوناتشي بالأرقام الثلاثة و ، و . في كتاب المربعات ، الذي نشره فيبوناتشي في وقت لاحق من نفس العام ، قام بحل المسألة العامة المتمثلة في إيجاد ثلاثة أعداد مربعة متباعدة بشكل متساوٍ عن بعضها البعض ، مشكلاً متتالية حسابية . وصف فيبوناتشي الفجوة بين هذه الأعداد بأنها متطابقة . [2] تتمثل إحدى طرق وصف حل فيبوناتشي في أن الأعداد المراد تربيعها هي فرق الأضلاع والوتر ومجموع أضلاع مثلث فيثاغورس ، وأن التطابق يساوي أربعة أضعاف مساحة المثلث نفسه. [3] لاحظ فيبوناتشي أنه من المستحيل أن يكون التطابق عددًا مربعًا بحد ذاته ، لكنه لم يقدم برهاناً مرضيًا على هذه الحقيقة. [4]
ملاحظات
المراجع
- Edwards (2000). Many subsequent mathematicians published proofs, including Gottfried Wilhelm Leibniz (1678), Leonhard Euler (1747), and Bernard Frenicle de Bessy (before 1765); see Dickson (1920) and Goldstein (1995).
- Bradley (2006).
- Beiler (1964).
- Ore (2012); Dickson (1920).
- بوابة نظرية الأعداد