مجموعة ماندلبرو
مجموعة ماندلبرو (بالإنجليزية: Mandelbrot set) هي شكل كسيري مشهور بشكل واسع حتى خارج مجال الرياضيات لتداخلها مع ما يدعى الفن الكسيري حيث تقدم صورا فنية تتميز بالجمال والتجريدية. ما يميز مجموعة ماندلبرو هو البنية المعقدة التي تقدمها رغم بساطة تعريفها. ترتبط مجموعة ماندلبرو ارتباطا شديدا بمجموعات جوليا (اللائي يحتوين على أشكال شبيهة من حيث التعقد). سميت هاته المجموعة هكذا نسبة إلى بونوا ماندلبرو، الذي درسها وشَهَرَها.


التاريخ
لمجموعة ماندلبرو مكانها في الديناميكا العقدية, وهو مجال بُحث فيه لأول مرة من طرف عالمي الرياضيات الفرنسيين بيير فاتو وغاستون جوليا في بداية القرن العشرين. أول صورة لهاته الكسيرية رُسمت من طرف روبرت وولف بروكس وبيتر ماتلسكي، وكان ذلك في عام 1978, كجزء من دراسة للزمر الكلاينية.[1] في أول يوم من مارس عام 1980، رأى ماندلبرو رسما للمجموعة لأول مرة, وكان ذلك في مختبر ينتمى إلى آي بي إم يقع في نيويورك في الولايات المتحدة.
درس ماندلبرو فضاء البارمترات لمتعددات الحدود التربيعية في مقالة ظهرت عام 1980.[2]
لكن الدراسة الرياضية الحقيقية لمجموعة ماندلبرو بدأت مع عمل كل من أدريان دوادي وجون ه. هوبارد John H. Hubbard[3] اللذان قاما بتأسيس وإيضاح العديد من خواص ، وأسمياها مجموعة ماندلبرو تكريما لماندلبرو.
التعريف الرسمي
تُعرف مجموعة ماندلبرو بواسطة مجموعة متعددات الحدود التربيعية العقدية
حيث
و c وسيط عقدي. بالنسبة لقيمة معينة للوسيط c، يُنظر إلى تصرف المتتالية التالية
التي يُحصل عليها عندما تُحسب بشكل متكرر ابتداء من النقطة الحرجة . لهاته المتتالية إمكانيتان أولاهما التباعد إلى ما لا نهاية له, ثانيتهما البقاء داخل قرص مركزه هو مركز المعلم وشعاعه هو عدد معين.
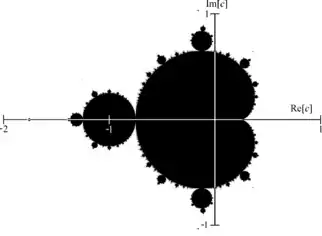
الخصائص الابتدائية
مجموعة ماندلبرو هي مجموعة مضغوطة, محتوية داخل القرص ذي الشعاع المساوي لاثنين والمتمركز في أصل المَعلم. هكذا، نقطة ما تنتمي إلى مجوعة ماندلبرو إذا وفقط إذا توفر ما يلي:
- مهما كان .
وبتعبير آخر، إذا وُجدت قيمة ما ل n حيث القيمة المطلقة ل تكون أكبر من اثنين، فإن المتتالية تؤول إلى ما لا نهاية له.

تقاطع M مع محور الأعداد الحقيقية هو بالتحديد المجال [-2, 0.25].
انظر إلى متتالية لوجستية.
تُقدر مساحة مجموعة ماندلبرو ب 1.50659177 ± 0.00000008.[4]
معرض صور
انظر أيضًا
مراجع
- Robert Brooks and Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in "Riemann Surfaces and Related Topics", ed. Kra and Maskit, Ann. Math. Stud. 97, 65–71, ISBN 0-691-08264-2
- Benoît Mandelbrot, Fractal aspects of the iteration of for complex , Annals NY Acad. Sci. 357, 249/259
- Adrien Douady and John H. Hubbard, Étude dynamique des polynômes complexes, Prépublications mathémathiques d'Orsay 2/4 (1984 / 1985)
- Mrob.com نسخة محفوظة 17 يونيو 2017 على موقع واي باك مشين.
- بوابة رياضيات
- بوابة هندسة رياضية



