Truncated trihexagonal tiling

Kisrhombille tiling
Kisrhombille tiling
Type	Dual semiregular tiling
Faces	30-60-90 triangle
Coxeter diagram
Symmetry group	p6m, [6,3], (*632)
Rotation group	p6, [6,3]+, (632)
Dual polyhedron	truncated trihexagonal tiling
Face configuration	V4.6.12
Properties	face-transitive

In geometry, the truncated trihexagonal tiling is one of eight semiregular tilings of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{3,6}.

An equilateral variation with rhombi instead of squares, and isotoxal hexagons instead of regular

Truncated trihexagonal tiling

Type	Semiregular tiling
Vertex configuration	4.6.12
Schläfli symbol	tr{6,3} or $t{\begin{Bmatrix}6\\3\end{Bmatrix}}$
Wythoff symbol	2 6 3 \|
Coxeter diagram
Symmetry	p6m, [6,3], (*632)
Rotation symmetry	p6, [6,3]⁺, (632)
Bowers acronym	Othat
Dual	Kisrhombille tiling
Properties	Vertex-transitive

Names

The name truncated trihexagonal tiling is analogous to truncated cuboctahedron and truncated icosidodecahedron, and misleading in the same way. An actual truncation of the trihexagonal tiling has rectangles instead of squares, and its hexagonal and dodecagonal faces can not both be regular.

Alternate interchangeable names are:

Great rhombitrihexagonal tiling
Rhombitruncated trihexagonal tiling
Omnitruncated hexagonal tiling, omnitruncated triangular tiling
Conway calls it a truncated hexadeltille.[1]

Trihexagonal tiling and its truncation

Uniform colorings

There is only one uniform coloring of a truncated trihexagonal tiling, with faces colored by polygon sides. A 2-uniform coloring has two colors of hexagons. 3-uniform colorings can have 3 colors of dodecagons or 3 colors of squares.

	1-uniform	2-uniform	3-uniform
Coloring
Symmetry	p6m, [6,3], (*632)	p3m1, [3^[3]], (*333)

Related 2-uniform tilings

The truncated trihexagonal tiling has three related 2-uniform tilings, one being a 2-uniform coloring of the semiregular rhombitrihexagonal tiling. The first dissects the hexagons into 6 triangles. The other two dissect the dodecagons into a central hexagon and surrounding triangles and square, in two different orientations.[2][3]

Semiregular	Dissections	Semiregular	2-uniform		3-uniform

Dual	Insets

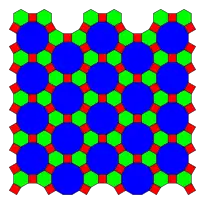
Circle packing

The Truncated trihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing number).[4]

Kisrhombille tiling

The kisrhombille tiling or 3-6 kisrhombille tiling is a tiling of the Euclidean plane. It is constructed by congruent 30-60-90 triangles with 4, 6, and 12 triangles meeting at each vertex.

Subdividing the faces of these tilings creates the kisrhombille tiling. (Compare the disdyakis hexa-, dodeca- and triacontahedron, three Catalan solids similar to this tiling.)

The kisrhombille tiling under its dual (left) and under the floret pentagonal tiling (right), from which it can be created as a partial truncation.

Construction from rhombille tiling

Conway calls it a kisrhombille[1] for his kis vertex bisector operation applied to the rhombille tiling. More specifically it can be called a 3-6 kisrhombille, to distinguish it from other similar hyperbolic tilings, like 3-7 kisrhombille.

It can be seen as an equilateral hexagonal tiling with each hexagon divided into 12 triangles from the center point. (Alternately it can be seen as a bisected triangular tiling divided into 6 triangles, or as an infinite arrangement of lines in six parallel families.)

It is labeled V4.6.12 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 12 triangles.

Symmetry

The kisrhombille tiling triangles represent the fundamental domains of p6m, [6,3] (*632 orbifold notation) wallpaper group symmetry. There are a number of small index subgroups constructed from [6,3] by mirror removal and alternation. [1⁺,6,3] creates *333 symmetry, shown as red mirror lines. [6,3⁺] creates 3*3 symmetry. [6,3]⁺ is the rotational subgroup. The commutator subgroup is [1⁺,6,3⁺], which is 333 symmetry. A larger index 6 subgroup constructed as [6,3*], also becomes (*333), shown in blue mirror lines, and which has its own 333 rotational symmetry, index 12.

Small index subgroups [6,3] (*632)
Index	1	2		3	6
Diagram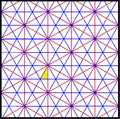
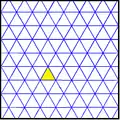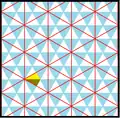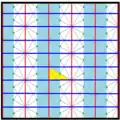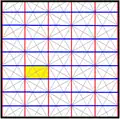Intl (orb.) Coxeter	p6m (*632) [6,3] = =	p3m1 (*333) [1⁺,6,3] = =	p31m (3*3) [6,3⁺] =	cmm (2*22)	pmm (*2222)	p3m1 (333) [6,3] = =
Direct subgroups
Index	2	4		6	12
Diagram
Intl (orb.) Coxeter	p6 (632) [6,3]⁺ = =	p3 (333) [1⁺,6,3⁺] = =		p2 (2222)	p2 (2222)	p3 (333) [1⁺,6,3*] = =

Related polyhedra and tilings

There are eight uniform tilings that can be based from the regular hexagonal tiling (or the dual triangular tiling). Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)

Uniform hexagonal/triangular tilings
Symmetry: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6³	3.12²	(3.6)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Uniform duals

V6³	V3.12²	V(3.6)²	V6³	V3⁶	V3.4.6.4	V.4.6.12	V3⁴.6	V3⁶

Symmetry mutations

This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedra), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

n32 symmetry mutation of omnitruncated tilings: 4.6.2n*
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
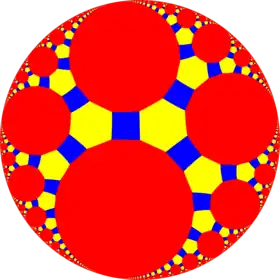Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Notes

Conway, 2008, Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table
Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
"Uniform Tilings". Archived from the original on 2006-09-09. Retrieved 2006-09-09.
Order in Space: A design source book, Keith Critchlow, p.74-75, pattern D

References

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 41. ISBN 0-486-23729-X.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern G, Dual p. 77-76, pattern 4
Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–56

External links

Weisstein, Eric W. "Uniform tessellation". MathWorld.
Weisstein, Eric W. "Semiregular tessellation". MathWorld.
Klitzing, Richard. "2D Euclidean tilings x3x6x - othat - O9".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[conway2008-1] Conway, 2008, Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table

[2] Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.

[3] "Uniform Tilings". Archived from the original on 2006-09-09. Retrieved 2006-09-09.

[Critchlow-4] Order in Space: A design source book, Keith Critchlow, p.74-75, pattern D