Tetraapeirogonal tiling
In geometry, the tetraapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of r{∞,4}.
| tetraapeirogonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (4.∞)2 |
| Schläfli symbol | r{∞,4} or rr{∞,∞} or |
| Wythoff symbol | 2 | ∞ 4 ∞ | ∞ 2 |
| Coxeter diagram | |
| Symmetry group | [∞,4], (*∞42) [∞,∞], (*∞∞2) |
| Dual | Order-4-infinite rhombille tiling |
| Properties | Vertex-transitive edge-transitive |
Uniform constructions
There are 3 lower symmetry uniform construction, one with two colors of apeirogons, one with two colors of squares, and one with two colors of each:
| Symmetry | (*∞42) [∞,4] |
(*∞33) [1+,∞,4] = [(∞,4,4)] |
(*∞∞2) [∞,4,1+] = [∞,∞] |
(*∞2∞2) [1+,∞,4,1+] |
|---|---|---|---|---|
| Coxeter | ||||
| Schläfli | r{∞,4} | r{4,∞}1⁄2 | r{∞,4}1⁄2=rr{∞,∞} | r{∞,4}1⁄4 |
| Coloring |  |
 |
 |
 |
| Dual |  |
 |
 |
 |
Symmetry
The dual to this tiling represents the fundamental domains of *∞2∞2 symmetry group. The symmetry can be doubled by adding mirrors on either diagonal of the rhombic domains, creating *∞∞2 and *∞44 symmetry.
Related polyhedra and tiling
| *n42 symmetry mutations of quasiregular tilings: (4.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *4n2 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracompact | Noncompact | |||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[ni,4] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
|
| Config. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.ni)2 |
| Paracompact uniform tilings in [∞,4] family | |||||||
|---|---|---|---|---|---|---|---|
 |
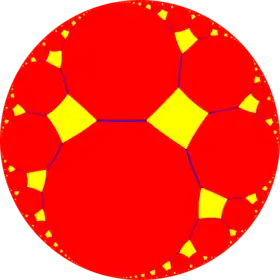 |
 |
 |
 |
 |
 | |
| {∞,4} | t{∞,4} | r{∞,4} | 2t{∞,4}=t{4,∞} | 2r{∞,4}={4,∞} | rr{∞,4} | tr{∞,4} | |
| Dual figures | |||||||
 |
 |
 |
 |
 |
 |
 | |
| V∞4 | V4.∞.∞ | V(4.∞)2 | V8.8.∞ | V4∞ | V43.∞ | V4.8.∞ | |
| Alternations | |||||||
| [1+,∞,4] (*44∞) |
[∞+,4] (∞*2) |
[∞,1+,4] (*2∞2∞) |
[∞,4+] (4*∞) |
[∞,4,1+] (*∞∞2) |
[(∞,4,2+)] (2*2∞) |
[∞,4]+ (∞42) | |
= |
= |
||||||
| h{∞,4} | s{∞,4} | hr{∞,4} | s{4,∞} | h{4,∞} | hrr{∞,4} | s{∞,4} | |
 |
 |
 |
 | ||||
| Alternation duals | |||||||
 |
 |
||||||
| V(∞.4)4 | V3.(3.∞)2 | V(4.∞.4)2 | V3.∞.(3.4)2 | V∞∞ | V∞.44 | V3.3.4.3.∞ | |
| Paracompact uniform tilings in [∞,∞] family | ||||||
|---|---|---|---|---|---|---|
= = |
= = |
= = |
= = |
= = |
= |
= |
 |
 |
 |
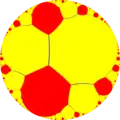 |
 |
 |
 |
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Dual tilings | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Alternations | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
 |
 |
 |
 |
 |
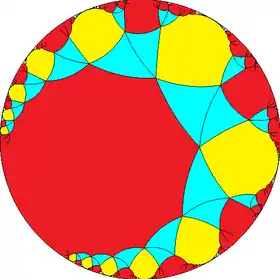 | |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Alternation duals | ||||||
 |
 |
 |
 | |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
See also
Wikimedia Commons has media related to Uniform tiling 4-i-4-i.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, "The Hyperbolic Archimedean Tessellations")
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

