Spherical polyhedron

In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.

The most familiar spherical polyhedron is the football, thought of as a spherical truncated icosahedron.
This beach ball would be a hosohedron with 6 spherical lune faces, if the 2 white caps on the ends were removed.

The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron.

Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, {2, 6}, is a hosohedron, and {6, 2} is its dual dihedron.

History

The first known man-made polyhedra are spherical polyhedra carved in stone. Many have been found in Scotland, and appear to date from the neolithic period (the New Stone Age).

During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) wrote the first serious study of spherical polyhedra.

Two hundred years ago, at the start of the 19th Century, Poinsot used spherical polyhedra to discover the four regular star polyhedra.

In the middle of the 20th Century, Coxeter used them to enumerate all but one of the uniform polyhedra, through the construction of kaleidoscopes (Wythoff construction).

Examples

All regular polyhedra, semiregular polyhedra, and their duals can be projected onto the sphere as tilings:

Schläfli
symbol		 {p,q} t{p,q} r{p,q} t{q,p} {q,p} rr{p,q} tr{p,q} sr{p,q}
Vertex
configuration		 pq q.2p.2p p.q.p.q p.2q.2q qp q.4.p.4 4.2q.2p 3.3.q.3.p
Tetrahedral
symmetry
(3 3 2)
33
3.6.6
3.3.3.3
3.6.6
33
3.4.3.4
4.6.6
3.3.3.3.3

V3.6.6
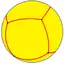V3.3.3.3
V3.6.6
V3.4.3.4
V4.6.6
V3.3.3.3.3
Octahedral
symmetry
(4 3 2)
43
3.8.8
3.4.3.4
4.6.6
34
3.4.4.4
4.6.8
3.3.3.3.4

V3.8.8
V3.4.3.4
V4.6.6
V3.4.4.4
V4.6.8
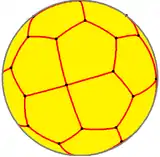V3.3.3.3.4
Icosahedral
symmetry
(5 3 2)
53
3.10.10
3.5.3.5
5.6.6
35
3.4.5.4
4.6.10
3.3.3.3.5

V3.10.10
V3.5.3.5
V5.6.6
V3.4.5.4
V4.6.10
V3.3.3.3.5
Dihedral
example p=6
(2 2 6)
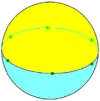62
2.12.12
2.6.2.6
6.4.4
26
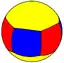2.4.6.4
4.4.12
3.3.3.6
Tiling of the sphere by spherical triangles (icosahedron with some of its spherical triangles distorted).
n 2 3 4 5 6 7 8 10 ...
n-Prism
(2 2 p)		 ...
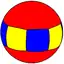n-Bipyramid
(2 2 p)		 ...
n-Antiprism ...
n-Trapezohedron ...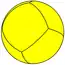

Improper cases

Spherical tilings allow cases that polyhedra do not, namely hosohedra: figures as {2,n}, and dihedra: figures as {n,2}. Generally, regular hosohedra and regular dihedra are used.

Family of regular hosohedra · *n22 symmetry mutations of regular hosohedral tilings: nn
Space SphericalEuclidean
Tiling name (Monogonal)
Henagonal hosohedron		 Digonal hosohedron (Triangular)
Trigonal hosohedron		 (Tetragonal)
Square hosohedron		 Pentagonal hosohedron Hexagonal hosohedron Heptagonal hosohedron Octagonal hosohedron Enneagonal hosohedron Decagonal hosohedron Hendecagonal hosohedron Dodecagonal hosohedron ... Apeirogonal hosohedron
Tiling image ...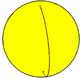
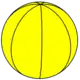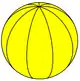Schläfli symbol {2,1}{2,2}{2,3}{2,4}{2,5}{2,6}{2,7}{2,8}{2,9}{2,10}{2,11}{2,12}...{2,∞}
Coxeter diagram ...
Faces and edges 123456789101112...∞
Vertices 2...2
Vertex config. 22.223242526272829210211212...2∞
Family of regular dihedra · *n22 symmetry mutations of regular dihedral tilings: nn
Space SphericalEuclidean
Tiling name (Hengonal)
Monogonal dihedron		 Digonal dihedron (Triangular)
Trigonal dihedron		 (Tetragonal)
Square dihedron		 Pentagonal dihedron Hexagonal dihedron ... Apeirogonal dihedron
Tiling image ...
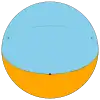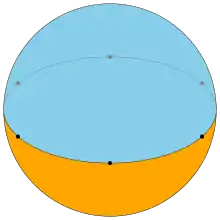Schläfli symbol {1,2}{2,2}{3,2}{4,2}{5,2}{6,2}...{∞,2}
Coxeter diagram ...
Faces 2 {1}2 {2}2 {3}2 {4}2 {5}2 {6}...2 {∞}
Edges and vertices 123456...∞
Vertex config. 1.12.23.34.45.56.6...∞.∞

Relation to tilings of the projective plane

Spherical polyhedra having at least one inversive symmetry are related to projective polyhedra[1] (tessellations of the real projective plane) – just as the sphere has a 2-to-1 covering map of the projective plane, projective polyhedra correspond under 2-fold cover to spherical polyhedra that are symmetric under reflection through the origin.

The best-known examples of projective polyhedra are the regular projective polyhedra, the quotients of the centrally symmetric Platonic solids, as well as two infinite classes of even dihedra and hosohedra:[2]

See also
Wikimedia Commons has media related to Spherical polyhedra.

References
  1. McMullen, Peter; Schulte, Egon (2002). "6C. Projective Regular Polytopes". Abstract Regular Polytopes. Cambridge University Press. pp. 162–5. ISBN 0-521-81496-0.
  2. Coxeter, H.S.M. (1969). "§21.3 Regular maps'". Introduction to Geometry (2nd ed.). Wiley. pp. 386–8. ISBN 978-0-471-50458-0. MR 0123930.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.