11-celdas
En matemáticas, un 11-celdas (o hendecacorón) es un 4-politopo regular abstracto autodual (un tipo de polícoro, es decir, de politopo en cuatro dimensiones). Sus 11 celdas son hemicosaedros. Posee 11 vértices, 55 aristas y 55 caras.[1] Su tipo de Schläfli es {3,5,3}, con 3 hemicosaedros (tipo de Schläfli {3,5}) alrededor de cada arista.
| 11-celdas | |
|---|---|
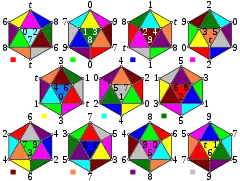 Los 11 hemicosaedros con vértices etiquetados por índices 0..9,t. Las caras están coloreadas por la celda a la que se conectan, definidas por los pequeños cuadros de colores | |
| Tipo | 4-politopos regulares abstractos |
| Celdas | 11 hemicosaedros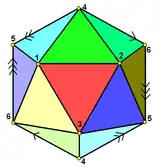 |
| Caras | 55 {3} |
| Aristas | 55 |
| Vértices | 11 |
| Figura de vértice | Hemidodecaedro |
| Símbolo de Schläfli | {3,5,3} |
| Grupo de simetría | Orden 660 L2(11) abstracto |
| Dual | Autodual |
| Propiedades | Regular |
Posee un orden de simetría de 660, calculado como el producto del número de celdas (11) y la simetría de cada celda (60). Su estructura de simetría es la del grupo abstracto lineal proyectivo especial L2(11).
Fue descubierto en 1977 por Branko Grünbaum, quien lo construyó pegando hemi-icosaedros, tres en cada arista, hasta que la forma se cerró. Fue descubierto de forma independiente por Harold Scott MacDonald Coxeter en 1984, quien estudió su estructura y simetría con mayor profundidad.
Politopos relacionados

Proyección ortogonal de un 10-símplex, con 11 vértices y 55 aristas.
El 11-celdas abstracto contiene el mismo número de vértices y de aristas que el 10-símplex de 10 dimensiones, y posee 1/3 de sus 165 caras. Por lo tanto, se puede dibujar como una figura regular en el espacio de 10 dimensiones, aunque sus celdas hemi-icosaédricas están sesgadas; es decir, cada celda no está contenida dentro de un subespacio tridimensional plano.
Véase también
- 5-símplex
- 57-celdas
- Panal icosaédrico, un panal hiperbólico regular con el mismo tipo de Schläfli {3,5,3}
Referencias
- Weisstein, Eric W. «11-celdas». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Bibliografía
- Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0
- Coxeter, H.S.M., A Symmetrical Arrangement of Eleven hemi-Icosahedra, Annals of Discrete Mathematics 20 pp103–114.
- The Classification of Rank 4 Locally Projective Polytopes and Their Quotients, 2003, Michael I Hartley
Enlaces externos
- J. Lanier, Jaron’s World. Discover, April 2007, pp 28-29.
- Klitzing, Richard. «Explanations Grünbaum-Coxeter Polytopes».
- 2007 ISAMA paper: Hyperseeing the Regular Hendecachoron, Carlo H. Séquin & Jaron Lanier, Also Isama 2007, Texas A&m hyper-Seeing the Regular Hendeca-choron. (= 11-Cell)