57-celdas
En matemáticas, un 57 celdas (o pentacontacaiheptacorón) es un 4-politopo regular abstracto autodual (un tipo de polícoro, es decir, de politopo en cuatro dimensiones). Sus 57 celdas son hemidodecaedros, y posee 57 vértices, 171 aristas y 171 caras bidimensionales.[1]
| 57-cell | |
|---|---|
| Tipo | 4-politopo regular abstracto |
| Celdas | 57 hemidodecaedros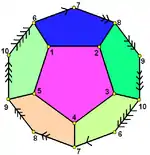 |
| Caras | 171 {5} |
| Aristas | 171 |
| Vértices | 57 |
| Figura de vértice | Hemicosaedro |
| Tipo de Schläfli | {5,3,5} |
| Grupo de simetría | Orden 3420 L2(19) abstracto |
| Dual | Autodual |
| Propiedades | Regular |
Su orden de simetría es 3420, como resultado del producto del número de celdas (57) y la simetría de cada celda (60). Su estructura de simetría es la del grupo abstracto lineal proyectivo especial L2(19).
Tiene tipo de Schläfli {5,3,5}, con 5 celdas hemidodecaédricas alrededor de cada arista. Fue descubierto por Coxeter, 1982.
Grafo de Perkel

Los vértices y las aristas forman un grafo de Perkel, el único grafo de distancia regular con matriz de intersección {6,5,2;1,1,3}, descubierto por Perkel, 1979.
Véase también
- 11-celdas, politopo regular abstracto con celdas hemicosaédricas.
- Hecatonicosacoron: 4 politopos regulares con células dodecaédricas
- Panal dodecaédrico de orden-5: panal hiperbólico regular con el mismo tipo de Schläfli, {5,3,5}.
Referencias
- Weisstein, Eric W. «57-celdas». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Bibliografía
- Coxeter, H. S. M. (1982), «Ten toroids and fifty-seven hemidodecahedra», Geometriae Dedicata 13 (1): 87-99, MR 679218, S2CID 120672023, doi:10.1007/BF00149428..
- McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications 92, Cambridge: Cambridge University Press, pp. 185-186, 502, ISBN 0-521-81496-0, MR 1965665, doi:10.1017/CBO9780511546686.
- Perkel, Manley (1979), «Bounding the valency of polygonal graphs with odd girth», Canadian Journal of Mathematics 31 (6): 1307-1321, MR 553163, doi:10.4153/CJM-1979-108-0..
- Séquin, Carlo H.; Hamlin, James F. (2007), «The Regular 4-dimensional 57-cell», ACM SIGGRAPH 2007 Sketches, SIGGRAPH '07, New York, NY, USA: ACM, S2CID 37594016, doi:10.1145/1278780.1278784.
- La clasificación de politopos proyectivos locales de rango 4 y sus cocientes, 2003, Michael I Hartley
Enlaces externos
- Siggraph 2007: 11-cell and 57-cell by Carlo Sequin
- Klitzing, Richard. «Explanations Grünbaum-Coxeter Polytopes».
- Weisstein, Eric W. «Perkel graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Perkel graph