Algoritmo de propagación de creencias

Representación parcial de un factor graph. Resulta útil imaginarse que dentro de los nodos factores (cuadrados) radica una función ${\displaystyle f_{a}(x_{a})}$ que expresa la interacción entre las variables que residen en su vecindad

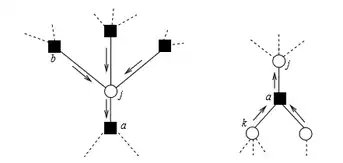
Existen variantes del algoritmo de propagación de creencias para diferentes modelos gráficos (Redes bayesianas, y campos aleatorios de Markov). El modelo gráfico usado en adelante es llamado factor graph, esto no representa ninguna limitación pues estos modelos son equivalentes y es posible la conversión entre estos.[7] Un factor graph es un grafo bipartito con dos tipos de nodos: nodos variables, usualmente denotados por las letras ${\displaystyle i,j,k,...}$ y representados gráficamente con círculos, y nodos factores, usualmente denotados por las letras ${\displaystyle a,b,c,...}$ y representados gráficamente como cuadrados, existe una arista entre un nodo variable ${\displaystyle i}$ y un nodo función ${\displaystyle a}$ si y solo si ${\displaystyle i}$ se encuentra en el argumento de ${\displaystyle f_{a}(x_{a})}$ . Llamaremos ${\displaystyle V}$ al conjunto de nodos variables y ${\displaystyle F}$ al conjunto de los nodos factores.

El algoritmo funciona enviando “mensajes” entre los nodos variables y nodos factores. De forma más específica si ${\displaystyle i\in V}$ y ${\displaystyle a\in F}$ el mensaje enviado desde ${\displaystyle i}$ hacia ${\displaystyle a}$ es la evaluación de una función ${\displaystyle n:V\to \mathbb {R} }$ y de forma alterna el mensaje enviado desde ${\displaystyle a}$ hacia ${\displaystyle i}$ es la evaluación de una función ${\displaystyle m:F\to \mathbb {R} }$. Estos mensajes contiene la influencia de una variable sobre otra. El cálculo de los mensajes posee diferente forma según los nodos emisores y receptores.

Un mensaje enviado desde una variable ${\displaystyle i}$ a un nodo función ${\displaystyle a}$ es el producto de todos los mensajes que recibe la variable ${\displaystyle i}$ de los nodos factores vecinos ${\displaystyle b}$ excepto ${\displaystyle a}$.${\displaystyle n_{i\to a}(x_{i})=\prod _{b\in N(i)/a}m_{b\to i}(x_{i})}$donde ${\displaystyle N(i)/a}$ es el conjunto de los nodos factores vecinos de ${\displaystyle i}$ a excepción del nodo ${\displaystyle a}$. Si este conjunto es vació entonces ${\displaystyle n_{i\to a}(x_{i})}$distribuye de uniformemente sobre el conjunto de valores posibles de la variable ${\displaystyle i}$.

Un mensaje enviado desde un nodo factor ${\displaystyle a}$ hacia un nodo variable ${\displaystyle i}$ es el producto de la función ${\displaystyle f_{a}(x_{a})}$ evaluada en la vecindad de ${\displaystyle a}$ a excepción de ${\displaystyle i}$ que esta marginalizado al valor ${\displaystyle x_{i}}$.${\displaystyle m_{a\to i}(x_{i})=\sum _{x_{a}/x_{i}}f_{a}(x_{a})\prod _{j\in N(a)/i}n_{j\to i}(x_{j})}$Si ${\displaystyle N(a)/i}$ es vacío entonces ${\displaystyle m_{a\to i}(x_{i})=f_{a}(x_{i})}$. La suma sobre ${\displaystyle x_{a}/x_{i}}$ es la suma sobre todo el conjunto de todos los posibles valores de las variables vecinas de ${\displaystyle a}$ a excepción de ${\displaystyle i}$ que se encuentra marginalizada al valor ${\displaystyle x_{i}}$.

Inicialmente el conjunto de mensajes iniciales se escogen de manera aleatoria, luego siguiendo cierto esquema iterativo de actualización (usualmente tomar un nodo aleatorio y actualizar los mensajes a sus vecinos) con respectos a los mensajes anteriores se computan los nuevos mensajes. Si el modelo gráfico posee forma de árbol, existe un esquema de actualización que garantiza convergencia (ver siguiente sección). Si se cumple que el proceso converge, usualmente que los mensajes dejen de cambiar, que no se garantiza en grafos generales, es posible obtener la distribución marginal computada por la propagación de creencias.

La distribución marginal estimada de cada nodo variable es proporcional al producto de los mensajes de los nodos vecinos.${\displaystyle P(x_{i})={\frac {1}{\alpha _{v}}}\prod _{a\in N(i)}m_{a\to i}(x_{i})}$En el caso de los nodos función la distribución conjunta de las variables que son parte de su vecindad es proporcional al mensaje recibido por el nodo.${\displaystyle P(x_{a})={\frac {1}{\alpha _{f}}}f_{a}(x_{a})\prod _{a\in N(i)}n_{i\to a}(x_{i})}$donde ${\displaystyle \alpha _{v}}$ y ${\displaystyle \alpha _{f}}$ son constantes de normalización${\displaystyle \alpha _{v}=\sum _{x_{i}}\prod _{a\in N(i)}m_{a\to i}(x_{i})}$${\displaystyle \alpha _{f}=\sum _{x_{a}}f(x_{a})\prod _{i\in N(a)}n_{i\to a}(x_{i})}$

Factor Graph que representa la siguiente función de probabilidad conjunta:${\textstyle p(x)=p_{a}(x_{1},x_{2})p_{b}(x_{2},x_{3},x_{4})p_{c}(x_{4})}$

En el caso de que el modelo gráfico sea un árbol, el algoritmo de propagación de creencias computa de manera exacta los marginales, siguiendo un esquema específico de actualización de mensaje, este esquema termina luego de 2 iteraciones. El esquema de actualización se describe a continuación:

Antes de comenzar, es seleccionado un nodo como nodo raíz y cualquier nodo no raíz que se encuentra conectado a un solo nodo es llamado hoja.

En la primera iteración los mensajes son inicialmente computados en las hojas y “suben” en la estructura hasta alcanzar la raíz. La estructura de árbol garantiza que es posible obtener todos los mensajes de los vecinos de cada nodo, excepto de uno de ellos, que será el que recibirá el mensaje.

La segunda iteración se compone de enviar los mensajes de forma contraria, comenzando en la raíz y haciéndolos “descender” hasta las hojas. El algoritmo termina cuando todas las hojas hayan recibido su mensaje.[8]

Como ejemplo concreto del cálculo exacto de los marginales en árboles consideremos la distribución de probabilidad dada en la figura superior. Usando repetidamente las ecuaciones de propagación de creencias encontramos que:

${\displaystyle P(x_{1})=\alpha m_{a\to i}(x_{1})}$

${\displaystyle P(x_{1})=\alpha \sum _{x_{2}}f_{a}(x_{1},x_{2})n_{2\to a}(x_{2})}$

${\displaystyle P(x_{1})=\alpha \sum _{x_{2}}f_{a}(x_{1},x_{2})m_{b\to 2}(x_{2})}$

${\displaystyle P(x_{1})=\alpha \sum _{x_{2}}\sum _{x_{3}}\sum _{x_{4}}f_{a}(x_{1},x_{2})f_{b}(x_{2},x_{3},x_{4})n_{3\to b}(x_{3})n_{4\to b}(x_{4})}$

${\displaystyle P(x_{1})=\alpha \sum _{x_{2}}\sum _{x_{3}}\sum _{x_{4}}f_{a}(x_{1},x_{2})f_{b}(x_{2},x_{3},x_{4})m_{c\to 4}(x_{4})}$

${\displaystyle P(x_{1})=\alpha \sum _{x_{2}}\sum _{x_{3}}\sum _{x_{4}}f_{a}(x_{1},x_{2})f_{b}(x_{2},x_{3},x_{4})f_{c}(x_{4})}$

Que es exactamente la definición de probabilidad marginal y su factor de normalización ${\displaystyle \alpha }$.

El algoritmo de propagación de creencias fue diseñado para modelos gráficos acíclicos (árboles), se ha comprobado que es posible usarlo en grafos generales, este algoritmo usualmente es llamado algoritmo “cíclico” de propagación de creencias debido a que estos grafos contienen ciclos. La inicialización y los esquemas de actualización son diferentes del esquema anterior visto en árboles, debido a que estos grafos pueden no contener hojas. Es necesario establecer un número de iteración mucho mayor que las dos iteraciones necesarias para convergencia en árboles.

La condición general bajo la cual el algoritmo de propagación de creencias puede converger no es totalmente entendida, es conocido que un grafo con un solo ciclo converge en la mayoría de los casos, pero la estimación de los marginales puede ser incorrecta. Existen varias condiciones suficientes, pero no necesarias, sobre la convergencia en un grafo con ciclos; también se conocen grafos en los cuales no resulta posible la convergencia. Técnicas como EXIT Chart pueden proveer una visualización aproximada del progreso de la propagación de creencias para la convergencia.

Existen otros métodos de aproximación para el cálculo de marginales como los métodos Variacionales y los métodos de Monte Carlo. Un método para el computo de marginales en grafos generales es el algoritmo junction tree. Este es la aplicación de Belief Propagation sobre un grafo modificado a través de la eliminación de ciclos agrupándolos en un nodo para obtener la estructura de árbol.[9]

Un algoritmo similar al de propagación de creencias es el llamado algoritmo de Viterbi, el cual resuelve el problema de maximización o de explicación más probable. En vez de solucionar el cómputo del marginal, el objetivo radica en el cálculo de los valores que maximiza la función global es decir los valores más probables en una configuración de ${\displaystyle X}$. La diferencia fundamental radica en reemplazar la suma por la maximización.

${\displaystyle m_{a\to i}(x_{i})=\max _{x_{a}/x_{i}}f(x_{a})\prod _{j\in N(a)/i}n_{j\to a}(x_{i})}$

Propagación de creencias con decimación aplicada al problema de coloreado de grafo con 3 colores y distintos grados de conectividad. La figura muestra la probabilidad de encontrar una asignación de colores válida en función del grado de conectividad. La propagación de creencias basada en la decimación es capaz de encontrar soluciones para valores mayores de ${\displaystyle c=4}$, donde la propagación de creencias estima de forma incorrecta los marginales o no converge.

La propagación de creencias computa, o en grafos generales aproxima, probabilidades marginales. En algunos problemas, los marginales proveen la solución de manera directa, por ejemplo en corrección de errores en códigos,[10] en el problema de emparejamiento,[11][12] o en modelo de Ising con campo aleatorio a temperatura cero,[13][14] etc.

En los problemas de satisfacción de restricciones, en general, los marginales no brindan de forma directa información acerca de la solución. Por ejemplo en coloreado de grafos, con ${\displaystyle q}$ colores, las ecuaciones de BP siempre convergen a marginales uniformes ${\displaystyle {\frac {1}{q}}}$, esta es la solución correcta pero no brinda ninguna información útil. Un intento por solucionar esto es el algoritmo de propagación de creencias con decimación.

En cada ciclo del algoritmo con decimación, las ecuaciones de propagación de creencias son actualizadas hasta que estas convergen o se alcanza el número máximo de iteraciones. Luego se sigue alguna estrategia de elección de variables, dos de ellas son:

• Decimación uniforme: Escoger una variable con probabilidad uniforme y asignar un valor según la probabilidad estimada por la propagación de creencias.
• Decimación maximal: Encontrar la variable con mayor probabilidad hacia algún estado y asignarle dicho estado.

El algoritmo descrito posee una complejidad cuadrática. En la práctica una cantidad pequeña de variables deben ser decimadas en cada iteración, con el objetivo de reducir esta complejidad a tiempo linear, si el tiempo máximo de convergencia crece como ${\displaystyle O(logN)}$. En el problema de coloreado de grafos con 3 y 4 colores, la propagación de creencias basada en la decimación mejora la estimación de marginales respecto de la propagación de creencias.[15]

El cálculo de marginales pertenece a la clase #P-Completo, esta clase se cree que posee problemas más difícil que la clases NP-Completo,[16] y el de maximización a la clase NP-Completo. Ambos problemas pertenecen a la clase NP-Hard.

Es posible reducir la memoria necesaria, o complejidad espacial, del algoritmo de propagación de creencias a través del uso del algoritmo de Islas, a costo de un pequeño aumento en la complejidad temporal.

La propagación de creencias está relacionada con el cálculo de la energía libre en termodinámica.[2] Supongamos que ${\displaystyle p(x)}$ es la verdadera distribución de probabilidad de un sistema, y esta cumple la ley de Boltzmann.

${\displaystyle p_{\beta }(x)={\frac {1}{Z}}e^{-\beta E(x)}}$

y ${\displaystyle \beta }$ es el inverso de la temperatura.

La energía del estado ${\displaystyle x}$ es:

${\displaystyle E(x)=-\sum _{a=1}^{M}\ln f_{a}(x_{a})}$

La energía libre de este sistema es:

${\displaystyle F_{H}=-\ln Z}$

La determinación de esta permite el análisis de diferentes características del sistema entre ellas: la energía promedio de una configuración para una temperatura dada. Por esto se han desarrollado varias aplicaciones para la aproximación a este valor.

Supongamos que introducimos una distribución de probabilidad ${\displaystyle b(x)}$ de prueba y su correspondiente energía libre variacional definida por:

${\displaystyle F(b)=U(b)-H(b)}$

Donde ${\displaystyle U(b)}$ es la energía variacional promedio

${\displaystyle U(b)=\sum _{x\in S}b(x)E(x)}$

y ${\displaystyle H(b)}$ es la entropía variacional

${\displaystyle H(b)=-\sum _{x\in S}b(x)\ln b(x)}$

Según las definiciones anteriores

${\displaystyle F(b)=F_{H}+D(b||p)}$

Donde

${\displaystyle D(b||P)=\sum _{x\in S}\ln {\frac {b(x)}{p(x)}}}$

Es la "medida" de Kullback–Leibler entre ${\displaystyle b(x)}$ y ${\displaystyle p(x)}$. Esta siempre es no negativa y es igual a cero si y solo si ${\displaystyle b(x)=p(x)}$. Minimizar la energía libre variacional ${\displaystyle E(b)}$ respecto a la distribución de prueba ${\displaystyle b(x)}$ es un procedimiento exacto para la determinación de ${\displaystyle F_{H}}$. y recuperación de ${\displaystyle p(x)}$ . Cuando el tamaño del sistema posee dimensiones grandes este procedimiento se vuelve intratable. Es posible establecer una cota superior a ${\displaystyle F_{H}}$ a través de la minimización de ${\displaystyle F(b)}$ imponiendo una restricción sobre las posibles familias de distribuciones de probabilidad que puede ser ${\displaystyle b(x)}$. Esta es la idea principal de la aproximación de campo medio.

Una de las elecciones más utilizadas es suponer que ${\displaystyle b(x)}$ es factorizable sobre las variables del sistema:

${\displaystyle b_{MF}(x)=\prod _{i=1}^{n}b_{i}(x_{i})}$

Donde cada ${\displaystyle b_{i}(x)}$ es una función de probabilidad sobre una única variable. Usando esta ${\displaystyle b_{MF}(x)}$ y la función de energía ${\displaystyle E(x)}$ para el factor graph, es posible computar la energía libre en la aproximación de campo medio.

${\displaystyle F_{MF}=U_{MF}-H_{MF}}$

${\displaystyle U_{MF}({\{b_{1},...,b_{n}\}})=-\sum _{a=1}^{M}\sum _{x_{a}}\ln f_{a}(x_{a})\prod _{i\in N(a)}b_{i}(x_{i})}$

${\displaystyle H_{MF}({\{b_{1},...,b_{n}\}})=-\sum _{i=1}^{N}b_{i}(x_{i})\ln b_{i}(x_{i})}$

Es posible considerar el uso de otras familias de funciones más complejas, para reducir la cota superior de la aproximación de campo medio respecto a la energía libre.[2]

Es posible mostrar que los mensajes luego de la convergencia de la propagación de creencias son útiles en la construcción de configuraciones que minimizan la energía libre de dicho sistema, si el modelo gráfico posee estructura de árbol, en caso de tener ciclos el modelo gráfico solo se puede afirmar que es un punto estacionario en la aproximación de energía libre.

Las regiones son conjuntos de variables y nodos factores de un factor graph, tal que todas las variables conectadas a un nodo factor incluido se encuentran incluidas. Los conjuntos compuestos por los nodos {1,2} y {B, C, 2, 3, 4} pueden ser regiones pero el conjunto {B,3} no, pues los nodos {2,4} no pertenecen a este conjunto

El algoritmo de propagación de creencias se suele representar como un algoritmo de paso de mensaje entre los nodos del modelo gráfico. En el caso de factor graph los mensajes son trasmitidos entre los nodos variables y los nodos funciones. Considerando el envió de mensajes entre regiones (conjuntos que pueden tener más de un nodo) es una forma de generalizar este algoritmo. Existen varias maneras de definir las regiones del modelo gráfico que intercambiaran mensajes; una de ellas plantea que una región es un conjunto de variables y nodos factores tal que si un nodo factor pertenece a una región, entonces las variables en su vecindario también pertenecen a esta región. Uno de estos métodos usa las ideas introducidas por Kikuchi en la literatura física y es conocido como el Método de variación de cluster de Kikuchi.

Los métodos de generalización de propagación de creencias permiten mejorar las aproximaciones y las propiedades de convergencia, a costo de un incremento en la complejidad, según la elección de las regiones.[2][6] La elección de regiones que optimicen la complejidad es un tema de investigación actualmente abierto.

Mejoras en las aproximaciones de propagación de creencias son alcanzables a través de la ruptura de las réplicas en la distribución de los campos (mensajes). Esta generalización permitió la creación de un nuevo tipo de algoritmo llamado Survey Propagation el cual ha probado ser muy útil en problemas en la clase NP-Completos como satisfacibilidad booleana[17] y cubrimiento mínimo en grafos.[18] Es conocido que el algoritmo de propagación de sondeos es la aplicación del algoritmo de propagación de creencias sobre una clase especial de objetos combinatorios llamados covers, en su aplicación al problema de la satisfacibilidad booleana.[19][20]

La propagación de creencias con distribución gaussiana es una variante del algoritmo de propagación de creencias donde las distribuciones de los mensajes son gaussianas. El primer trabajo en analizar este modelo especial fue realizado por Weiss y Freeman.[21]

${\displaystyle P(x_{i})={\frac {1}{Z}}\int _{i\neq j}e^{-{\frac {1}{2}}x^{T}Ax+b^{T}x}dx_{i}}$

Donde ${\displaystyle Z}$ es una constante de normalización,${\displaystyle A}$ es matriz simétrica definida positiva y ${\displaystyle b}$ es un vector de desplazamiento.

Equivalentemente puede ser mostrado que usando el modelo gaussiano, la solución al problema de marginalización es equivalente al problema MAP.

${\displaystyle \arg \max _{x}P(x)={\frac {1}{z}}e^{-{\frac {1}{2}}x^{T}Ax+b^{T}x}}$

Este problema es además equivalente al problema de minimización cuadrática:

${\displaystyle \min _{x}{\frac {1}{2}}x^{T}Ax-b^{T}x}$

Que es a la vez equivalente al sistema de ecuación linear

${\displaystyle Ax=b}$

La convergencia de la propagación de creencias con distribución gaussiana es relativamente más fácil de analizar (respecto al modelo general de propagación de creencias) y existen dos condiciones suficientes de convergencia. La primera de estas fue formulada por Weiss y colaboradores en el 2000, que garantiza la convergencia cuando la matriz A es diagonalmente dominante, y la segunda fue formulada por Johnson y colaboradores en 2006 que asegura la convergencia cuando el radio espectral de la matriz cumple

${\displaystyle \rho (I-|D^{-{\frac {1}{2}}}AD|)<1}$

Donde ${\displaystyle D=diag(A)}$y ${\displaystyle I}$ es la matriz identidad.

Posteriormente Su y Wu establecieron condiciones necesarias y suficientes.[22]

Es posible vincular el algoritmo de propagación de creencias con distribución gaussiana al dominio de álgebra lineal y fue mostrado como un algoritmo iterativo para la solución de sistemas de ecuaciones lineales ${\displaystyle Ax=b}$. Experimentos muestran que la propagación de creencias con distribución gaussiana converge más rápido que otros métodos iterativos clásicos como el método de Jacobi, el método de Gauss-Seidel[23] y posee buena tolerancia a los problemas numéricos del método del gradiente conjugado de precondición.[24]