Cuboide (geometría)
En geometría, un cuboide es un hexaedro, un sólido de seis caras. Sus caras son cuadriláteros. Cuboide significa "como un cubo". Un cuboide es como un cubo en el sentido de que ajustando las longitudes de las aristas o los ángulos entre caras un cuboide puede transformarse en un cubo. En lenguaje matemático un cuboide es un poliedro convexo cuyo grafo poliédrico es igual al de un cubo.
Un caso especial de cuboide es el cuboide rectangular, llamado ortoedro, con 6 rectángulos como caras. Sus caras adyacentes se encuentran en ángulos rectos. Un caso especial de cuboide rectangular es un cubo con seis caras cuadradas que forman ángulos rectos.[1][2]
Cuboides generales
Por la fórmula de Euler el número de caras F, de vértices V, y de aristas E de cualquier poliedro convexo están relacionados por la fórmula F + V = E + 2. En el caso de un cuboide esto da 6 + 8 = 12 + 2; es decir, como un cubo, un cuboide tiene 6 caras, 8 vértices, y 12 aristas. Junto con los cuboides rectangulares, cualquier paralelepípedo es un cuboide de este tipo, al igual que un tronco cuadrado ,la forma formada por el truncamiento del vértice de una pirámide cuadrada.
| Hexaedro de caras cuadriláteras (cuboide): 6 caras, 12 aristas, 8 vértices | ||||||
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| Cubo (cuadrados) |
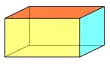
Cuboide rectangular (tres pares de rectángulos) |
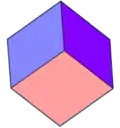
Trapezoedro trigonal (rombos congruentes) |
Trapezoedro trigonal (cuadriláteros congruentes) |
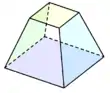
Quadrilátero frustum (vértice truncado pirámide cuadrada) |
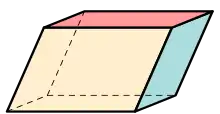
Paralelepípedo (tres pares de paralelogramos) |
Romboedro (tres pares de rombos) |
| Oh, [4,3], (*432) orden 48 |
D2h, [2,2], (*222) orden 8 |
D3d, [2+,6], (2*3) orden 12 |
D3, [2,3]+, (223) orden 6 |
C4v, [4], (*44) orden 8 |
Ci, [2+,2+], (×) orden 2 | |
Cuboide rectangular
| Cuboide rectangular | |
|---|---|
 | |
| Tipo | Prisma Plesioedro |
| Caras | 6 rectángulos |
| Aristas | 12 |
| Vértices | 8 |
| Simetría de grupo | D2h, [2,2], (*222), orden 8 |
| Símbolo de Schläfli | { } × { } × { } |
| Diagrama de Coxeter-Dynkin | |
| Poliedro conjugado | Fusil rectangular |
| Propiedades | Convexo, zonoedro, isogonal |
En un cuboide rectangular, todos los ángulos son ángulos rectos, y las caras opuestas de un cuboide son iguales. Por definición, esto lo convierte en un prisma rectangular, y los términos paralelepípedo rectangular o paralelepípedo ortogonal también se utilizan para designar este poliedro. Los términos prisma rectangular y prisma oblongo, sin embargo, son ambiguos, ya que no especifican todos los ángulos.
El cuboide cuadrado, caja cuadrada o prisma cuadrado recto (también llamado ambiguamente prisma cuadrado) es un caso especial del cuboide en el que al menos dos caras son cuadrados. Tiene símbolo de Schläfli {4} × { }, y su simetría es doble de [2,2] a [4,2], orden 16.
El cubo es un caso especial del cuboide cuadrado en el que las seis caras son cuadrados. Tiene símbolo de Schläfli {4,3}, y su simetría se eleva de [2,2], a [4,3], orden 48.
Si las dimensiones de un cuboide rectangular son a, b y c, entonces su volumen es abc y su superficie es 2(ab + ac + bc).
La longitud de la diagonal espacial es:
Las formas cuboides se utilizan a menudo para cajas, armarios, habitaciones, edificios, contenedores, armarios, libros, un robusto chasis de ordenador, dispositivos de impresión, dispositivos electrónicos de pantalla táctil, lavadoras y secadoras, calefactores, etc. Los cuboides se encuentran entre los sólidos que pueden tesselar el espacio tridimensional. La forma es bastante versátil al poder contener múltiples cuboides más pequeños, por ejemplo terrones de azúcar en una caja, cajas en un armario, armarios en una habitación y habitaciones en un edificio.
Un cuboide con aristas enteras así como diagonales enteras en las caras se llama ladrillo de Euler, por ejemplo, con caras 44, 117 y 240. Un cuboide perfecto es un ladrillo de Euler cuya diagonal espacial también es un número entero. Actualmente se desconoce si existe un cuboide perfecto.
Redes
El número de redes diferentes para un cubo simple es 11. Sin embargo, este número aumenta significativamente hasta (al menos) 54 para un cuboide rectangular de 3 longitudes diferentes.
Véase también
Referencias
- Robertson, Stewart Alexander (1984). Polytopes and Symmetry. Cambridge University Press. p. 75. ISBN 9780521277396.
- Dupuis, Nathan Fellowes (1893). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Consultado el 1 de diciembre de 2018.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Cuboide.
Wikimedia Commons alberga una categoría multimedia sobre Cuboide.- Weisstein, Eric W. «Cuboid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Rectangular prism and cuboid Modelos de papel e imágenes