Diagrama de Dynkin

El interés fundamental de los diagramas de Dynkin es que clasifican álgebras de Lie semisimples sobre cuerpos algebraicamente cerrados. Tales álgebras de Lie se clasifican a través de su sistema de raíces, que puede representarse mediante un diagrama de Dynkin, de acuerdo con las restricciones que deben cumplir, como se describe a continuación.

Prescindir de la dirección en los enlaces del grafo corresponde a reemplazar un sistema raíz por el grupo de reflexión finito que genera, el llamado Grupo de Weyl, y por lo tanto, los diagramas de Dynkin no dirigidos clasifican los grupos de Weyl.

Presentan la siguiente correspondencia para las álgebras de Lie asociadas a grupos clásicos sobre los números complejos:

• ${\displaystyle A_{n}:}$ ${\displaystyle {\mathfrak {sl}}_{n+1}}$, el álgebra de Lie lineal especial.
• ${\displaystyle B_{n}:}$ ${\displaystyle {\mathfrak {so}}_{2n+1}}$, el grupo ortogonal de dimensión impar.
• ${\displaystyle C_{n}:}$ ${\displaystyle {\mathfrak {sp}}_{2n}}$, el álgebra de Lie simpléctica.
• ${\displaystyle D_{n}:}$ ${\displaystyle {\mathfrak {so}}_{2n}}$, el grupo ortogonal de dimensión par (${\displaystyle n>1}$).

Para los grupos excepcionales, los nombres del álgebra de Lie y del diagrama de Dynkin asociado coinciden.

Los diagramas de Dynkin se pueden interpretar como una clasificación de muchos objetos distintos relacionados entre sí, y la notación "A_n, B_n, ..." se utiliza para referirse a "todas" tales interpretaciones, según el contexto. El carácter ambiguo de esta notación puede generar interpretaciones confusas.

Su caracterización central implica que un álgebra de Lie simple tiene un sistema raíz, al que está asociado un diagrama de Dynkin (orientado); y por ejemplo, los tres pueden denominarse B_n.

El diagrama de Dynkin no orientado es una forma de diagrama de Coxeter, y corresponde al grupo de Weyl, que es el grupo de reflexión finito asociado al sistema raíz. Por lo tanto, B_n puede referirse al diagrama no orientado (un tipo especial de diagrama de Coxeter), al grupo de Weyl (un grupo de reflexión concreto) o al grupo abstracto de Coxeter.

Aunque el grupo de Weyl es abstractamente isomorfo al grupo de Coxeter, un isomorfismo específico depende de una elección ordenada de raíces simples.

Téngase en cuenta también que, si bien la notación del diagrama de Dynkin está estandarizada, el diagrama de Coxeter y la notación de grupo varían, y en algunas ocasiones concuerdan con la notación del diagrama de Dynkin y en otras no.

Por último, los objetos asociados "a veces" se denominan con la misma notación, aunque esto no siempre se puede hacer regularmente. Entre los ejemplos de esta circunstancia, se incluyen:

• La retícula raíz generada por el sistema raíz, como en el caso de la retícula E₈, que se define naturalmente, pero no elemento a elemento. Por ejemplo, A₂ y G₂ generan ambos una retícula hexagonal.
• Un politopo asociado: por ejemplo, el politopo de Gosset 4₂₁ puede denominarse "politopo E₈", ya que sus vértices se derivan del sistema raíz E₈ y tiene el grupo E₈ de Coxeter como grupo de simetría.
• Una forma cuadrática asociada o múltiple: por ejemplo, la variedad E₈ tiene una forma de intersección dada por la red E₈.

Estas últimas notaciones se usan principalmente para objetos asociados con diagramas excepcionales; los objetos asociados a los diagramas regulares (A, B, C, D) tienen nombres tradicionales.

El índice (la letra n) es igual al número de nodos en el diagrama, el número de raíces simples en una base, la dimensión de la red reticular y el tramo del sistema raíz, el número de generadores del grupo de Coxeter, y el rango del álgebra de Lie. Sin embargo, n no equivale a la dimensión del módulo de definición (una representación fundamental) del álgebra de Lie: el índice del diagrama de Dynkin no debe confundirse con el índice del álgebra de Lie. Por ejemplo, ${\displaystyle B_{4}}$ corresponde a ${\displaystyle {\mathfrak {so}}_{2\cdot 4+1}={\mathfrak {so}}_{9},}$ que actúa naturalmente en el espacio de 9 dimensiones, pero tiene el rango 4 como álgebra de Lie.

Los diagramas simplemente enlazados de Dynkin, aquellos sin enlaces múltiples (A, D, E) clasifican muchos objetos matemáticos adicionales.

Ejemplo: A2

El sistema raíz ${\displaystyle A_{2}}$,

Por ejemplo, el símbolo ${\displaystyle A_{2}}$ puede referirse a:

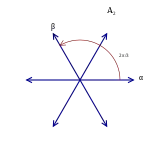
• El diagrama de Dynkin con 2 nodos conectados, , que también puede interpretarse como un diagrama de Coxeter.
• El sistema de raíces con 2 raíces simples en un ángulo de ${\displaystyle 2\pi /3}$ (120 grados).
• El álgebra de Lie ${\displaystyle {\mathfrak {sl}}_{2+1}={\mathfrak {sl}}_{3}}$ de rango 2.
• El grupo de Weyl de simetrías de las raíces (reflexiones en el hiperplano ortogonal a las raíces), isomorfo al grupo simétrico ${\displaystyle S_{3}}$ (de orden 6).
• El grupo de Coxeter abstracto, presentado por generadores y relaciones, ${\displaystyle \left\langle r_{1},r_{2}\mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1\right\rangle .}$

Considérese un sistema de raíces, que se supone reducido e integral (o "cristalográfico"). En muchas aplicaciones, este sistema raíz surgirá de un álgebra de Lie semisimple. Sea ${\displaystyle \Delta }$ un conjunto de raíces simples positivas. A continuación se construye un diagrama ${\displaystyle \Delta }$ de la manera que se explica a continuación.[1] Se forma un gráfico con un vértice para cada elemento de ${\displaystyle \Delta }$, y luego se insertan los enlaces entre cada par de vértices de acuerdo con la regla siguiente. Si las raíces correspondientes a los dos vértices son ortogonales, no hay enlace entre los vértices. Si el ángulo entre las dos raíces es de 120 grados, se coloca un enlace entre los vértices. Si el ángulo es de 135 grados, se colocan dos enlaces, y si el ángulo es de 150 grados, se coloca un enlace triple (estos cuatro casos agotan todos los ángulos posibles entre pares de raíces simples positivas).[2] Finalmente, si existen enlaces entre un par de vértices dado, se marcan con una flecha que apunta desde el vértice correspondiente a la raíz más larga hasta el vértice correspondiente a la más corta (la flecha se omite si las raíces tienen la misma longitud). Al pensar en la flecha como un signo "mayor que", queda claro en qué dirección debe ir la flecha. Los diagramas de Dynkin conducen a una clasificación de sistemas de raíces. Los ángulos y las relaciones de longitud entre las raíces están ligadas entre sí.[3] Por lo tanto, los enlaces de las raíces no ortogonales pueden describirse alternativamente como un enlace para una relación de longitud de 1, un enlace doble para una relación de longitud de ${\displaystyle {\sqrt {2}}}$ y un enlace triple para una relación de longitud de ${\displaystyle {\sqrt {3}}}$ (no se colocan enlaces cuando las raíces son ortogonales, independientemente de la relación de longitud).

En el sistema raíz A2, que se muestra a la derecha, las raíces etiquetadas ${\displaystyle \alpha }$ y ${\displaystyle \beta }$ forman una base. Dado que estas dos raíces tienen un ángulo de 120 grados (con una relación de longitud de 1), el diagrama de Dynkin consta de dos vértices conectados por un solo borde: .

Los diagramas de Dynkin deben satisfacer ciertas restricciones, esencialmente aquellas satisfechas por los diagramas de Coxeter–Dynkin finitos, junto con una restricción cristalográfica adicional.

Los diagramas de Dynkin están estrechamente relacionados con los diagramas de Coxeter-Dynkin de los Grupos de Coxeter finitos, y su terminología a menudo se combina.[nota 1]

Los diagramas de Dynkin difieren de los diagramas de Coxeter de grupos finitos en dos aspectos importantes:

Dirigido en parte

los diagramas de Dynkin son parcialmente dirigidos: cualquier enlace múltiple (en términos de Coxeter, etiquetado con "4" o superior) tiene una dirección (una flecha que apunta de un nodo al otro); así, los diagramas de Dynkin tienen "más" datos que los diagramas de Coxeter subyacentes (con gráficos no dirigidos).

En el nivel de los sistemas raíz, la dirección corresponde a apuntar hacia el vector más corto; los enlaces etiquetados como "3" no tienen dirección porque los vectores correspondientes deben tener la misma longitud. (Precaución: algunos autores invierten esta convención, con la flecha apuntando hacia el vector más largo).

Restricción cristalográfica

los diagramas de Dynkin deben satisfacer una restricción adicional, a saber, que las únicas etiquetas de enlace permitidas son 2, 3, 4 y 6, una restricción que no comparten los diagramas de Coxeter, por lo que no todos los diagramas de Coxeter de un grupo finito provienen de un diagrama de Dynkin.

En el nivel de los sistemas raíz, esto corresponde al teorema de restricción cristalográfica, ya que las raíces forman una retícula.

Otra diferencia, solo estilística, es que los diagramas de Dynkin se dibujan convencionalmente con enlaces dobles o triples entre nodos (para p = 4, 6), en lugar de con un enlace etiquetado con su grado de multiplicidad p.

El término "diagrama de Dynkin" a veces se refiere al gráfico "dirigido", y a veces al gráfico "no dirigido". Para mayor precisión, en este artículo "diagrama de Dynkin" significará "dirigido", y el gráfico subyacente no dirigido se denominará "diagrama de Dynkin no dirigido". Entonces los diagramas de Dynkin y los diagramas de Coxeter pueden relacionarse de la siguiente manera:

Esto significa que los diagramas de Coxeter de grupos finitos corresponden a grupos puntuales generados por reflexiones, mientras que los diagramas Dynkin deben satisfacer una restricción adicional correspondiente al teorema de restricción cristalográfica, y que los diagramas Coxeter no están dirigidos, mientras que los diagramas de Dynkin están (parcialmente) dirigidos.

Los objetos matemáticos correspondientes clasificados por los diagramas son:

El espacio en blanco en la parte superior derecha, correspondiente a gráficos dirigidos con un gráfico subyacente no dirigido a cualquier diagrama de Coxeter (de un grupo finito), se puede definir formalmente, pero se discute poco y no parece admitir una interpretación simple en términos de objetos matemáticos de interés.

Existen aplicaciones naturales hacia abajo, desde diagramas de Dynkin hasta diagramas de Dynkin no dirigidos; respectivamente, desde los sistemas raíz hasta los grupos Weyl asociados, y hacia la derecha, desde los diagramas de Dynkin no dirigidos hasta los diagramas de Coxeter; respectivamente de grupos Weyl a grupos Coxeter finitos.

La aplicación descendente está generada sobre (por definición), pero no elemento a elemento, ya que los diagramas B_n y C _n se asignan al mismo diagrama no dirigido, con el diagrama de Coxeter resultante, y por lo tanto el grupo de Weyl a veces es denotado BC_n.

La aplicación propia es simplemente una inclusión: los diagramas de Dynkin no dirigidos son casos especiales de los diagramas de Coxeter, y los grupos de Weyl son casos especiales de los grupos de Coxeter finitos, y no están sobre, ya que no todos los diagramas de Coxeter son diagramas de Dynkin no dirigidos (los diagramas perdidos son H₃,H₄ e I₂ (p) parap = 5 p ≥ 7), y en consecuencia, no todos los grupos de Coxeter finitos son un grupo de Weyl.

Los isomorfismos excepcionales de los diagramas de Dynkin conectados

Los diagramas de Dynkin están numerados de manera convencional para que la lista no sea redundante: ${\displaystyle n\geq 1}$ para ${\displaystyle A_{n},}$ ${\displaystyle n\geq 2}$ para ${\displaystyle B_{n},}$ ${\displaystyle n\geq 3}$ para ${\displaystyle C_{n},}$ ${\displaystyle n\geq 4}$ para ${\displaystyle D_{n},}$ y ${\displaystyle E_{n}}$ comenzando en ${\displaystyle n=6.}$ Las familias se pueden definir para un n menor, produciendo un isomorfismo excepcional de diagramas, e isomorfismos excepcionales correspondientes de álgebras de Lie y grupos de Lie asociados.

Trivialmente, se pueden comenzar las familias en ${\displaystyle n=0}$ o ${\displaystyle n=1,}$ que son isomórficas, ya que existe un diagrama vacío único y un diagrama único de 1 nodo. Los otros isomorfismos de los diagramas de Dynkin conectados son:

• ${\displaystyle A_{1}\cong B_{1}\cong C_{1}}$
• ${\displaystyle B_{2}\cong C_{2}}$
• ${\displaystyle D_{2}\cong A_{1}\times A_{1}}$
• ${\displaystyle D_{3}\cong A_{3}}$
• ${\displaystyle E_{3}\cong A_{1}\times A_{2}}$
• ${\displaystyle E_{4}\cong A_{4}}$
• ${\displaystyle E_{5}\cong D_{5}}$

Estos isomorfismos corresponden al isomorfismo de álgebras de Lie simples y semisimples, que también corresponden a ciertos isomorfismos de las formas grupales de Lie. También agregan contexto a familia de E_n.[4]

El diagrama de Dynkin más simétrico es D₄

Además del isomorfismo entre diferentes diagramas, algunos diagramas también poseen autoisomorfismos o "automorfismos". Los automorfismos de diagrama corresponden a automorfismos externos del álgebra de Lie, lo que significa que el grupo de automorfismo externo Out = Aut/Inn es igual al grupo de automorfismos de diagrama.[5][6][7]

Los diagramas que tienen automorfismos no triviales son A_n (${\displaystyle n>1}$), D_n (${\displaystyle n>1}$) y E₆. En todos estos casos, excepto D₄, existe un único automorfismo no trivial (Out = C₂, el grupo cíclico de orden 2), mientras que para D₄, el grupo de automorfismo es el grupo simétrico sobre tres letras (S₃, orden 6). Este fenómeno se conoce como "trialidad". Sucede que todos estos automorfismos de diagrama se pueden realizar como simetrías euclidianas de cómo se dibujan los diagramas convencionalmente en el plano, pero esto es solo un artefacto de cómo se dibujan, y no una estructura intrínseca en sí misma.

A_n

Para A_n, el automorfismo del diagrama está invirtiendo el diagrama, que es una recta. Los nodos del diagrama indexan los pesos fundamentales, que (para A_n−1) son ${\displaystyle \bigwedge ^{i}C^{n}}$ para ${\displaystyle i=1,\dots ,n}$, y el automorfismo del diagrama corresponde a la dualidad ${\displaystyle \bigwedge ^{i}C^{n}\mapsto \bigwedge ^{n-i}C^{n}.}$ Realizado como el álgebra de Lie ${\displaystyle {\mathfrak {sl}}_{n+1},}$, el automorfismo externo se puede expresar como transposición negativa, ${\displaystyle T\mapsto -T^{\mathrm {T} }}$, que es como actúa la representación dual.[6]

D_n

Para D_n, el diagrama de automorfismo es cambiar los dos nodos al final de la Y, y corresponde a cambiar las dos representaciones de espín quirales. Realizado como el álgebra de Lie ${\displaystyle {\mathfrak {so}}_{2n},}$, el automorfismo externo puede expresarse como conjugación mediante una matriz en O (2n) con determinante −1 ${\displaystyle \mathrm {A} _{3}\cong \mathrm {D} _{3},}$ por lo que sus automorfismos coinciden, mientras que ${\displaystyle \mathrm {D} _{2}\cong \mathrm {A} _{1}\times \mathrm {A} _{1},}$ está desconectado, y el automorfismo corresponde a cambiar los dos nodos.

Para D₄, la representación fundamental es isomorfa a las dos representaciones de espín, y el grupo simétrico resultante en tres letras (S₃, o alternativamente el grupo diedral de orden 6, Dih₃) corresponde tanto al automorfismo del álgebra de Lie como al automorfismo del diagrama.

E₆

El grupo de automorfismo de E₆ corresponde a invertir el diagrama, y puede expresarse usando álgebras de Jordan.[6][8]

Los diagramas desconectados, que corresponden a álgebras de Lie "semi"simples, pueden tener automorfismos por el intercambio de componentes del diagrama.

En característica 2, la flecha en F₄ puede ser ignorada, produciendo un diagrama adicional del automorfismo, correspondiente a los grupos de Suzuki-Ree

Con característica positiva existen "automorfismos de diagrama" adicionales: en términos generales, en la característica p a veces se permite ignorar la flecha en los enlaces de multiplicidad p en el diagrama de Dynkin correspondientes a los automorfismos de diagrama. Por lo tanto, en la característica 2 hay un automorfismo de orden 2 de ${\displaystyle \mathrm {B} _{2}\cong \mathrm {C} _{2}}$ y de F₄, mientras que en la característica 3 existe un automorfismo de orden 2 de G₂. Pero no se aplica en todas las circunstancias: por ejemplo, tales automorfismos no necesitan surgir como automorfismos del grupo algebraico correspondiente, sino en el nivel de puntos valorados en un campo finito.

Plegado

Plegados del grupo de Coxeter finito

Plegados del grupo de Coxeter afín, con las convenciones de denominación de árboles de elementos: primero, el conjunto extendido original; segundo, usado en el contexto de gráficos quiver; y el último, ideado por Victor Kac para álgebras de Lie afines torsionadas

Un diagrama de Dynkin (simple) (finito o afín) que tiene una simetría (que satisface una condición, según se detalla a continuación) puede ser estructurado en torno a una simetría, produciendo un nuevo diagrama generalmente de múltiples líneas, con el proceso llamado "plegado" '(debido a que la mayoría de las simetrías aparecen dos veces). A nivel de álgebras de Lie, esto corresponde a tomar el subálgebra invariante bajo el grupo de automorfismo externo, y el proceso se puede definir únicamente con referencia a los sistemas de raíces, sin usar diagramas.[9] Además, cada diagrama de múltiples cordones (finito o infinito) se puede obtener plegando un diagrama simple.[10]

La única condición en el automorfismo para que el plegado sea posible es que nodos distintos del gráfico en la misma órbita (bajo el automorfismo) no deben estar conectados por un enlace; a nivel de los sistemas de raíces, las raíces en la misma órbita deben ser ortogonales.[10] A nivel de los diagramas, esto es necesario, ya que de lo contrario el diagrama del cociente tendría un bucle, debido a la identificación de dos nodos pero con un enlace entre ellos, y los bucles no están permitidos en los diagramas de Dynkin.

Los nodos y enlaces del diagrama del cociente ("plegado") son las órbitas de los nodos y enlaces del diagrama original; los enlaces son únicos a menos que dos enlaces incidentes se asignen al mismo enlace (especialmente en los nodos de valencia mayores que 2): un "punto de ramificación" del mapa, en cuyo caso el peso es el número de enlaces incidentes y los puntos de flecha hacia el nodo en el que inciden: "el punto de ramificación se asigna al punto no homogéneo". Por ejemplo, en D₄ plegado a G₂, el enlace en G₂ apunta desde la clase de los 3 nodos externos (valencia 1) a la clase del nodo central (valencia 3).

Los pliegues de los diagramas finitos son:[11][nota 2]

• ${\displaystyle A_{2n-1}\to C_{n}}$ (el automorfismo de A_2n no produce un plegamiento porque los dos nodos centrales están conectados por un enlace, pero en la misma órbita).
• ${\displaystyle D_{n+1}\to B_{n}}$
• ${\displaystyle D_{4}\to G_{2}}$ (si está haciendo un cociente por el grupo completo o un ciclo 3, además de ${\displaystyle D_{4}\to B_{3}}$ de 3 formas diferentes, o si se está haciendo un cociente por una involución)
• ${\displaystyle E_{6}\to F_{4}}$

Existen plegamientos similares para diagramas afines, que incluyen:

• ${\displaystyle {\tilde {A}}_{2n-1}\to {\tilde {C}}_{n}}$
• ${\displaystyle {\tilde {D}}_{n+1}\to {\tilde {B}}_{n}}$
• ${\displaystyle {\tilde {D}}_{4}\to {\tilde {G}}_{2}}$
• ${\displaystyle {\tilde {E}}_{6}\to {\tilde {F}}_{4}}$

La noción de plegamientos también se puede aplicar de manera más general a diagramas de Coxeter;[12] en particular, se pueden generalizar los cocientes permitidos de los diagramas de Dynkin a H_n e I₂(p). Geométricamente, esto corresponde a las proyecciones de un politopo uniforme. Cabe destacar que cualquier diagrama de Dynkin simplemente entrelazado se puede plegar a I₂(h), donde h es el número de Coxeter, que corresponde geométricamente a la proyección al plano de Coxeter.

El plegado se puede aplicar para reducir las preguntas sobre álgebras de Lie (semisimples) a cuestiones sobre las de unión simple, junto con un automorfismo, que puede ser más simple que tratar las álgebras de unión múltiple directamente. Esto se puede hacer en la construcción de las álgebras de Lie semisimples, por ejemplo. Consúltese Desbordamiento matemático: plegado por automatismos para obtener más información.

Sistema raíz A2

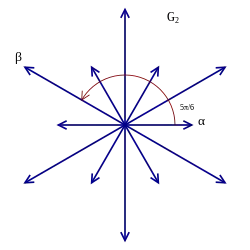Sistema raíz G2

Algunos mapas adicionales de diagramas tienen interpretaciones significativas, como se detalla a continuación. Sin embargo, no todos los mapas de sistemas raíz surgen como mapas de diagramas.[13]

Por ejemplo, hay dos inclusiones de sistemas de raíz de A₂ en G₂, ya sea como las seis raíces largas o las seis raíces cortas. Sin embargo, los nodos en el diagrama G₂ corresponden a una raíz larga y una raíz corta, mientras que los nodos en el diagrama A₂ corresponden a raíces de igual longitud y, por lo tanto, este mapa de sistemas raíz no puede expresarse como un mapa de los diagramas.

Algunas inclusiones de sistemas raíz se pueden expresar como un diagrama que es un subgrafo inducido de otro, que significa "un subconjunto de los nodos, con todos los enlaces entre ellos". Esto se debe a que eliminar un nodo de un diagrama de Dynkin corresponde a eliminar una raíz simple de un sistema raíz, lo que produce un sistema raíz de rango uno más bajo. Por el contrario, eliminar un enlace (o cambiar su multiplicidad) mientras se dejan los nodos sin cambios, corresponde a cambiar los ángulos entre las raíces, lo que no se puede hacer sin cambiar todo el sistema raíz. Por lo tanto, se pueden eliminar significativamente los nodos, pero no los enlaces. Eliminar un nodo de un diagrama conectado puede producir otro diagrama conectado (álgebra de Lie simple), si el nodo es una variedad, o un diagrama desconectado (un álgebra de Lie semisimple pero no simple), con dos o tres componentes (este último para D_n y E_n). Al nivel de las álgebras de Lie, estas inclusiones corresponden a las subálgebras de Lie.

Los subgrafos máximos son los siguientes (los relacionados por un diagrama de automorfismo están etiquetados como "conjugado"):

• A_n+1: A_n, en 2 formas conjugadas
• B_n+1: A_n, B_n
• C_n+1: A_n, C_n
• D_n+1: A_n (2 formas conjugadas), D_n
• E_n+1: A_n, D_n, E_n
  • Para E₆, dos de estos coinciden: ${\displaystyle \mathrm {D} _{5}\cong \mathrm {E} _{5}}$ y son conjugados
• F₄: B₃, C₃
• G₂: A₁, en 2 formas no conjugadas (como una raíz larga o una raíz corta)

Finalmente, la dualidad de los diagramas corresponde a invertir la dirección de las flechas, si las hay:[13] B_n y C_n son duales, mientras que F₄ y G₂ son auto-duales, al igual que los diagramas ADE de líneas simples.

Los diagramas de Dynkin simplemente entrelazados clasifican diversos objetos matemáticos (clasificación ADE)

Un diagrama de Dynkin sin enlaces múltiples se llama simplemente entrelazado, al igual que el álgebra de Lie y el grupo de Lie correspondientes. Estos son los diagramas ${\displaystyle A_{n},D_{n},E_{n}}$, y los fenómenos que clasifican tales diagramas se denominan clasificación ADE. En este caso, los diagramas de Dynkin coinciden exactamente con los diagramas de Coxeter, ya que no se incluyen enlaces múltiples.

Los diagramas de Dynkin clasifican álgebras de Lie semisimples complejas. Las álgebras de Lie semisimples reales se pueden clasificar como formas reales de álgebras de Lie semisimples complejas, y estas se clasifican por el diagrama de Satake, que se obtiene del diagrama de Dynkin etiquetando algunos vértices negros (rellenos) y conectando algunos otros vértices en pares por flechas, de acuerdo con ciertas reglas.

Eugene Dynkin

Los diagramas de Dynkin llevan el nombre de Eugene Dynkin, que los utilizó en dos documentos (1946, 1947) que simplifican la clasificación de álgebras de Lie semisimples;[14] ver (Dynkin, 2000). Cuando Dynkin abandonó la Unión Soviética en 1976, lo que por entonces se consideraba equivalente a la traición, se ordenó a los matemáticos soviéticos que se refirieran a "diagramas de raíces simples" en lugar de usar su nombre. ^{[cita requerida]}

Los gráficos no dirigidos habían sido utilizados anteriormente por Coxeter (1934) para clasificar los grupos de reflexión, donde los nodos correspondían a reflexiones simples; Witt (1941) utilizó los gráficos (con información de longitud) en referencia a los sistemas raíz, con los nodos correspondientes a raíces simples, tal como se usan hoy en día.[14][15] Dynkin los usó en 1946 y 1947, reconociendo a Coxeter y Witt en su artículo de 1947.

Los diagramas de Dynkin se han dibujado de distintas maneras.[15] La convención que se sigue aquí es la más común, con ángulos de 180° en los nodos de valencia 2, ángulos de 120° en el nodo de valencia 3 de D_n y ángulos de 90°/90°/180° en el nodo de valencia 3 de E_n, con multiplicidad indicada por 1, 2 o 3 enlaces paralelos, y longitud de raíz indicada dibujando una flecha en el enlace para indicar su orientación. Más allá de la simplicidad, un beneficio adicional de esta convención es que los automorfismos de diagrama son realizados por isometrías euclídeas de los diagramas.

La convención alternativa incluye escribir un número en el enlace para indicar multiplicidad (comúnmente usado en los diagramas de Coxeter), rellenar de negro los nodos para indicar la longitud de la raíz o usar ángulos de 120° en los nodos de valencia 2 para lograr que sean más distinguibles.

También hay convenciones sobre la numeración de los nodos. La convención moderna más común se había desarrollado en la década de 1960 y se ilustra en (Bourbaki, 1968).[15]

Los diagramas de Dynkin son equivalentes a las matrices de Cartan generalizadas, como se muestra en esta tabla de diagramas de Dynkin de rango 2 con sus correspondientes matrices de Cartan 2x2.

Para el rango 2, la forma de la matriz de Cartan es:

${\displaystyle A=\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}$

Un diagrama de varios enlaces corresponde a los elementos de la matriz de Cartan no diagonales -a₂₁, -a₁₂, con el número de enlaces dibujados igual a max(-a₂₁, -a₁₂), y una flecha apuntando hacia elementos que no son unitarios.

Una matriz de Cartan generalizada es una matriz cuadrada ${\displaystyle A=(a_{ij})}$ tal que:

1. Para entradas diagonales, ${\displaystyle a_{ii}=2}$.
2. Para entradas no diagonales, ${\displaystyle a_{ij}\leq 0}$.
3. ${\displaystyle a_{ij}=0}$ si y solo si ${\displaystyle a_{ji}=0}$

La matriz de Cartan determina si el grupo es de tipo finito (si es una matriz positiva-definida, es decir, todos sus valores propios son positivos), de tipo afín (si no es positiva-definida pero sí positiva-semidefinida, es decir, todos sus valores propios no son negativos) o de tipo indefinido. El tipo indefinido a menudo se subdivide aún más, por ejemplo, un grupo de Coxeter es Lorentziano si tiene un valor propio negativo y todos los demás valores propios son positivos. Además, varias fuentes se refieren a grupos Coxeter hiperbólicos, pero hay varias definiciones no equivalentes para este término. En la discusión que figura a continuación, los grupos de Coxeter hiperbólicos son un caso especial de los Lorentzianos, que satisfacen una condición adicional. Para el rango 2, todas las matrices de Cartan determinantes negativas corresponden al grupo de Coxeter hiperbólico. Pero en general, la mayoría de las matrices determinantes negativas no son ni hiperbólicas ni lorentzianas.

Las ramas finitas tienen (-a₂₁, -a₁₂) = (1,1), (2,1), (3,1), y las ramas afines (con un determinante cero) tienen (-a₂₁, -a₁₂) = (2, 2) o (4,1).

Diagramas de Dynkin de rango 2

Grupo Nombre	Diagrama de Dynkin			Matriz de Cartan		Orden de Simetría	Grupo3 Entrelazado simple Relacionado
	Grafo Multienlazado (Estándar)	Grafo1 con valores	Grafo2 Coxeter	${\displaystyle \left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}$	Determinante (4-a21*a12)
Finito (Determinante>0)
A1xA1				${\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}$	4	2
A2 (no dirigido)				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}$	3	3
B2				${\displaystyle \left[{\begin{smallmatrix}2&-2\\-1&2\end{smallmatrix}}\right]}$	2	4	${\displaystyle {A}_{3}}$
C2				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-2&2\end{smallmatrix}}\right]}$	2	4	${\displaystyle {A}_{3}}$
BC2 (no dirigido)				${\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}$	2	4
G2				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-3&2\end{smallmatrix}}\right]}$	1	6	${\displaystyle {D}_{4}}$
G2 (no dirigido)				${\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}$	1	6
Afín (Determinante=0)
A1(1)				${\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}$	0	∞	${\displaystyle {\tilde {A}}_{3}}$
A2(2)				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-4&2\end{smallmatrix}}\right]}$	0	∞	${\displaystyle {\tilde {D}}_{4}}$
Hiperbólico (Determinante<0)
				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-5&2\end{smallmatrix}}\right]}$	-1	-
				${\displaystyle \left[{\begin{smallmatrix}2&-2\\-3&2\end{smallmatrix}}\right]}$	-2	-
				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-6&2\end{smallmatrix}}\right]}$	-2	-
				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-7&2\end{smallmatrix}}\right]}$	-3	-
				${\displaystyle \left[{\begin{smallmatrix}2&-2\\-4&2\end{smallmatrix}}\right]}$	-4	-
				${\displaystyle \left[{\begin{smallmatrix}2&-1\\-8&2\end{smallmatrix}}\right]}$	-4	-
				${\displaystyle \left[{\begin{smallmatrix}2&-3\\-3&2\end{smallmatrix}}\right]}$	-5	-
				${\displaystyle \left[{\begin{smallmatrix}2&-b\\-a&2\end{smallmatrix}}\right]}$	4-ab<0	-
Nota1: Para grupos hiperbólicos, (a12*a21>4), el estilo de enlaces múltiples se sustituye por un etiquetado explícito (a21, a12) sobre el enlace. Por lo general, no se aplica a gráficos finitos y ni a afines.[16] Nota2: Para grupos no dirigidos, los diagramas de Coxeter son intercambiables. Por lo general, están etiquetados por su orden de simetría, con el orden 3 implícito sin etiqueta. Nota3: Se pueden obtener muchos grupos con enlaces múltiples a partir de un grupo de niveles simples de rango superior mediante la aplicación de una operación de plegado.

Existen extensiones de diagramas de Dynkin, como los diagramas afines de Dynkin, que clasifican las matrices de Cartan dentro de las álgebras de Lie afines. Estas a su vez se clasifican en (Kac, 1994, Chapter 4, pp. 47–), y son enumeradas específicamente en (Kac, 1994, pp. 53–55). Los diagramas afines se denotan como ${\displaystyle X_{l}^{(1)},X_{l}^{(2)},}$ o ${\displaystyle X_{l}^{(3)},}$ donde X es la letra del diagrama finito correspondiente, y el exponente depende de la serie de diagramas afines en los que se encuentren. En primer lugar, los ${\displaystyle X_{l}^{(1)},}$ son los más comunes y se denominan diagramas extendidos de Dynkin y se denotan con una virgulilla, y también a veces se marcan con un superíndice "+".[17] como en ${\displaystyle {\tilde {A}}_{5}=A_{5}^{(1)}=A_{5}^{+}}$. Las series (2) y (3) se denominan diagramas afines torsionados.

Consúltese el generador de diagramas de Dynkin para ver estos diagramas.

El conjunto de diagramas afines extendidos de Dynkin, con nodos agregados en verde (${\displaystyle n\geq 3}$ para ${\displaystyle B_{n}}$ y ${\displaystyle n\geq 4}$ para ${\displaystyle D_{n}}$)

Las formas afines "torsionadas" se denominan con los superíndices (2) o (3). (El subíndice k siempre cuenta el número de nodos amarillos en el gráfico, es decir, el número total de nodos menos 1)

En el artículo figuran todos los gráficos de Dynkin para grupos afines de hasta 10 nodos. Los gráficos extendidos de Dynkin se dan como las familias ~, lo mismo que los gráficos finitos anteriores, con un nodo agregado. Otras variaciones de gráfico dirigido se dan con un valor de superíndice (2) o (3), que representa plegamientos de grupos de orden superior. Estos se clasifican como diagramas afines torsionados.[18]

Gráficos de Dynkin afines conectados hasta (2 a 10 nodos)
(Agrupados como gráficos no dirigidos)

Rango	${\displaystyle {\tilde {A}}_{1+}}$	${\displaystyle {\tilde {B}}_{3+}}$	${\displaystyle {\tilde {C}}_{2+}}$	${\displaystyle {\tilde {D}}_{4+}}$	E / F / G
2	${\displaystyle {\tilde {A}}_{1}}$ o ${\displaystyle {A}_{1}^{(1)}}$		${\displaystyle {A}_{2}^{(2)}}$:
3	${\displaystyle {\tilde {A}}_{2}}$ o ${\displaystyle {A}_{2}^{(1)}}$		${\displaystyle {\tilde {C}}_{2}}$ o ${\displaystyle {C}_{2}^{(1)}}$ ${\displaystyle {D}_{5}^{(2)}}$: ${\displaystyle {A}_{4}^{(2)}}$:		${\displaystyle {\tilde {G}}_{2}}$ o ${\displaystyle {G}_{2}^{(1)}}$ ${\displaystyle {D}_{4}^{(3)}}$
4	${\displaystyle {\tilde {A}}_{3}}$ o ${\displaystyle {A}_{3}^{(1)}}$	${\displaystyle {\tilde {B}}_{3}}$ o ${\displaystyle {B}_{3}^{(1)}}$ ${\displaystyle {A}_{5}^{(2)}}$:	${\displaystyle {\tilde {C}}_{3}}$ o ${\displaystyle {C}_{3}^{(1)}}$ ${\displaystyle {D}_{6}^{(2)}}$: ${\displaystyle {A}_{6}^{(2)}}$:
5	${\displaystyle {\tilde {A}}_{4}}$ o ${\displaystyle {A}_{4}^{(1)}}$	${\displaystyle {\tilde {B}}_{4}}$ o ${\displaystyle {B}_{4}^{(1)}}$ ${\displaystyle {A}_{7}^{(2)}}$:	${\displaystyle {\tilde {C}}_{4}}$ o ${\displaystyle {C}_{4}^{(1)}}$ ${\displaystyle {D}_{7}^{(2)}}$: ${\displaystyle {A}_{8}^{(2)}}$:	${\displaystyle {\tilde {D}}_{4}}$ o ${\displaystyle {D}_{4}^{(1)}}$	${\displaystyle {\tilde {F}}_{4}}$ o ${\displaystyle {F}_{4}^{(1)}}$ ${\displaystyle {E}_{6}^{(2)}}$
6	${\displaystyle {\tilde {A}}_{5}}$ o ${\displaystyle {A}_{5}^{(1)}}$	${\displaystyle {\tilde {B}}_{5}}$ o ${\displaystyle {B}_{5}^{(1)}}$ ${\displaystyle {A}_{9}^{(2)}}$:	${\displaystyle {\tilde {C}}_{5}}$ o ${\displaystyle {C}_{5}^{(1)}}$ ${\displaystyle {D}_{8}^{(2)}}$: ${\displaystyle {A}_{10}^{(2)}}$:	${\displaystyle {\tilde {D}}_{5}}$ o ${\displaystyle {D}_{5}^{(1)}}$
7	${\displaystyle {\tilde {A}}_{6}}$ o ${\displaystyle {A}_{6}^{(1)}}$	${\displaystyle {\tilde {B}}_{6}}$ o ${\displaystyle {B}_{6}^{(1)}}$ ${\displaystyle {A}_{11}^{(2)}}$:	${\displaystyle {\tilde {C}}_{6}}$ o ${\displaystyle {C}_{6}^{(1)}}$ ${\displaystyle {D}_{9}^{(2)}}$: ${\displaystyle {A}_{12}^{(2)}}$:	${\displaystyle {\tilde {D}}_{6}}$ o ${\displaystyle {D}_{6}^{(1)}}$	${\displaystyle {\tilde {E}}_{6}}$ o ${\displaystyle {E}_{6}^{(1)}}$
8	${\displaystyle {\tilde {A}}_{7}}$ o ${\displaystyle {A}_{7}^{(1)}}$	${\displaystyle {\tilde {B}}_{7}}$ o ${\displaystyle {B}_{7}^{(1)}}$ ${\displaystyle {A}_{13}^{(2)}}$:	${\displaystyle {\tilde {C}}_{7}}$ o ${\displaystyle {C}_{7}^{(1)}}$ ${\displaystyle {D}_{10}^{(2)}}$: ${\displaystyle {A}_{14}^{(2)}}$:	${\displaystyle {\tilde {D}}_{7}}$ o ${\displaystyle {D}_{7}^{(1)}}$	${\displaystyle {\tilde {E}}_{7}}$ o ${\displaystyle {E}_{7}^{(1)}}$
9	${\displaystyle {\tilde {A}}_{8}}$ o ${\displaystyle {A}_{8}^{(1)}}$	${\displaystyle {\tilde {B}}_{8}}$ o ${\displaystyle {B}_{8}^{(1)}}$ ${\displaystyle {A}_{15}^{(2)}}$:	${\displaystyle {\tilde {C}}_{8}}$ o ${\displaystyle {C}_{8}^{(1)}}$ ${\displaystyle {D}_{11}^{(2)}}$: ${\displaystyle {A}_{16}^{(2)}}$:	${\displaystyle {\tilde {D}}_{8}}$ o ${\displaystyle {D}_{8}^{(1)}}$	${\displaystyle {\tilde {E}}_{8}}$ o ${\displaystyle {E}_{8}^{(1)}}$
10	${\displaystyle {\tilde {A}}_{9}}$ o ${\displaystyle {A}_{9}^{(1)}}$	${\displaystyle {\tilde {B}}_{9}}$ o ${\displaystyle {B}_{9}^{(1)}}$ ${\displaystyle {A}_{17}^{(2)}}$:	${\displaystyle {\tilde {C}}_{9}}$ o ${\displaystyle {C}_{9}^{(1)}}$ ${\displaystyle {D}_{12}^{(2)}}$: ${\displaystyle {A}_{18}^{(2)}}$:	${\displaystyle {\tilde {D}}_{9}}$ o ${\displaystyle {D}_{9}^{(1)}}$
11	...	...	...	...

Se enumera el conjunto de gráficos Dynkin hiperbólicos compactos y no compactos.[19] Todos los gráficos hiperbólicos de rango 3 son compactos. Los diagramas hiperbólicos compactos de Dynkin existen hasta el rango 5, y los gráficos hiperbólicos no compactos existen hasta el rango 10.

No compacto (formas sobre extendidas)

Algunas notaciones usadas en física teórica, como en la teoría M, usan un superíndice "+" para grupos extendidos en lugar de un "~" y esto permite definir grupos de extensiones más altas.

1. Extendido Los diagramas de Dynkin (afines) reciben "+" y representan un nodo agregado. (Igual que "~")
2. Diagramas de Dynkin sobreextendidos (hiperbólicos) reciben "^" o "++" y representan dos nodos agregados.
3. Muy extendido Los diagramas de Dynkin con 3 nodos agregados se dan como "+++".

Algunos ejemplos de diagramas de Dynkin sobreextendidos (hiperbólicos)

Rank	${\displaystyle {AE}_{n}}$ = An-2(1)^	${\displaystyle {BE}_{n}}$ = Bn-2(1)^ ${\displaystyle {CE}_{n}}$	Cn-2(1)^	${\displaystyle {DE}_{n}}$ = Dn-2(1)^	E / F / G
3	${\displaystyle {AE}_{3}}$:
4	${\displaystyle {AE}_{4}}$:		C2(1)^ A4(2)'^ A4(2)^ D3(2)^		G2(1)^ D4(3)^
5	${\displaystyle {AE}_{5}}$:	${\displaystyle {BE}_{5}}$ ${\displaystyle {CE}_{5}}$	C3(1)^ A6(2)^ A6(2)'^ D5(2)^
6	${\displaystyle {AE}_{6}}$	${\displaystyle {BE}_{6}}$ ${\displaystyle {CE}_{6}}$	C4(1)^ A8(2)^ A8(2)'^ D7(2)^	${\displaystyle {DE}_{6}}$	F4(1)^ E6(2)^
7	${\displaystyle {AE}_{7}}$	${\displaystyle {BE}_{7}}$ ${\displaystyle {CE}_{7}}$		${\displaystyle {DE}_{7}}$
8	${\displaystyle {AE}_{8}}$	${\displaystyle {BE}_{8}}$ ${\displaystyle {CE}_{8}}$		${\displaystyle {DE}_{8}}$	E6(1)^
9	${\displaystyle {AE}_{9}}$	${\displaystyle {BE}_{9}}$ ${\displaystyle {CE}_{9}}$		${\displaystyle {DE}_{9}}$	E7(1)^
10		${\displaystyle {BE}_{10}}$ ${\displaystyle {CE}_{10}}$		${\displaystyle {DE}_{10}}$	${\displaystyle {E}_{10}}$=E8(1)^