Factorial
El factorial de un entero positivo n, el factorial de n o n factorial se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n. Por ejemplo:
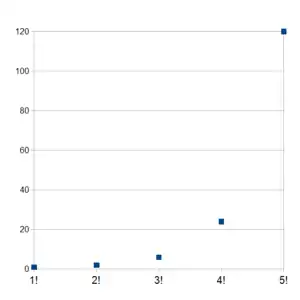
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40.320 |
| 9 | 362.880 |
| 10 | 3.628.800 |
| 15 | 1.307.674.368.000 |
| 20 | 2.432.902.008.176.640.000 |
| 25 | 15.511.210.043.330.985.984.000.000 |
| 50 | 30.414.093.201.713.378.043 × 10^45 |
| 70 | 1,19785717... × 10^100 |
| 450 | 1,73336873... × 10^1000 |
| 3.249 | 6,41233768... × 10^10 000 |
| 25.206 | 1,205703438... × 10^100 000 |
| 100.000 | 2,8242294079... × 10^456 573 |
La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en combinatoria y análisis matemático. De manera fundamental el factorial de n representa el número de formas distintas de ordenar n objetos distintos (elementos sin repetición). Este hecho ha sido conocido desde hace varios siglos, en el siglo XII por los estudiosos hindúes.
La definición de la función factorial también se puede extender a números no naturales manteniendo sus propiedades fundamentales, pero se requieren matemáticas avanzadas, particularmente del análisis matemático. El matemático francés Christian Kramp (1760-1826) fue la primera persona en usar la actual notación matemática n!, en 1808.[1]
Los factoriales han sido descubiertos en varias culturas antiguas, especialmente en las matemáticas indias en las obras canónicas de la literatura jainista, y por los místicos judíos en el libro talmúdico Sefer Yetzirah. La operación factorial se encuentra en muchas áreas de las matemáticas, sobre todo en combinatoria, donde su uso más básico cuenta las posibles secuencias distintas —las permutaciones— de objetos distintos: hay are . En análisis matemático, los factoriales se utilizan en series de potencias para la función exponencial y otras funciones, y también tienen aplicaciones en álgebra, teoría de números, teoría de la probabilidad e informática.
Gran parte de la matemática de la función factorial se desarrolló a partir de finales del siglo XVIII y principios del XIX. La aproximación de Stirling proporciona una aproximación exacta al factorial de los grandes números, demostrando que crece más rápidamente que el crecimiento exponencial. La fórmula de Legendre describe los exponentes de los números primos en una factorización prima de los factoriales, y puede utilizarse para contar los ceros finales de los factoriales. Daniel Bernoulli y Leonhard Euler interpolaron la función factorial a una función continua de números complejos, excepto en los enteros negativos, la función gamma (compensada).
Muchas otras funciones notables y secuencias de números están estrechamente relacionadas con los factoriales, incluyendo el coeficiente binomials, doble factorials, factorial descendentes, primorials, y subfactorials. Las implementaciones de la función factorial se utilizan habitualmente como ejemplo de diferentes estilos de programación informática, y se incluyen en calculadoras científicas y bibliotecas de software de cálculo científico. Aunque calcular directamente factoriales grandes utilizando la fórmula del producto o la recurrencia no es eficiente, se conocen algoritmos más rápidos, que igualan con un factor constante el tiempo de los algoritmos de multiplicación rápidos para números con el mismo número de dígitos.
Historia
El concepto de factoriales ha surgido de forma independiente en muchas culturas:
- En las matemáticas indias, una de las primeras descripciones conocidas de los factoriales proviene del Anuyogadvāra-sūtra,[2] una de las obras canónicas de la literatura jainista, a la que se han asignado fechas que varían entre 300 a. C. y 400 d. C.[3] Separa el orden ordenado e invertido de un conjunto de elementos de los otros órdenes ("mixtos"), evaluando el número de órdenes mixtos restando dos de la fórmula habitual del producto para el factorial. La regla del producto para permutaciones también fue descrita por el monje jainista del siglo VI de nuestra era Jinabhadra.[2] Los eruditos hindúes han estado utilizando fórmulas factoriales desde al menos 1150, cuando Bhāskara II mencionó factoriales en su obra Līlāvatī, en relación con un problema de cuántas maneras Vishnu podría sostener sus cuatro objetos característicos (un concha de concha, disco, maza, y flor de loto) en sus cuatro manos, y un problema similar para un dios de diez manos.[4]
- En las matemáticas de Oriente Medio, el libro místico hebreo de la creación Séfer Ietzirá', del Período talmúdico (200 a 500 CE), enumera factoriales ¡hasta 7! como parte de una investigación sobre el número de palabras que se pueden formar a partir del alfabeto hebreo.[5][6] Los factoriales también fueron estudiados por razones similares por el gramático árabe del siglo VIII Al-Khalil ibn Ahmad al-Farahidi.[5] El matemático árabe Ibn al-Haytham (también conocido como Alhazen, c. 965 - c. 1040) fue el primero en formular el teorema de Wilson que conecta los factoriales con los números primos.[7]
- En Europa, aunque las matemáticas griegas incluían algo de combinatoria, y Platón utilizó célebremente 5.040 (un factorial) como población de una comunidad ideal, en parte por sus propiedades de divisibilidad,[8] no hay evidencia directa del estudio de los factoriales en la Grecia antigua. En su lugar, el primer trabajo sobre factoriales en Europa fue realizado por eruditos judíos como Shabbethai Donnolo, explicando el pasaje del Sefer Yetzirah.[9] En 1677, el autor británico Fabian Stedman describió la aplicación de los factoriales al toque de cambios, un arte musical que consistía en hacer sonar varias campanas afinadas.[10][11]
A partir de finales del siglo XV, los factoriales se convirtieron en objeto de estudio de los matemáticos occidentales. En un tratado de 1494, el matemático italiano Luca Pacioli calculó factoriales hasta ¡11!, en relación con un problema de ordenación de mesas de comedor.[12] Christopher Clavius discutió los factoriales en un comentario de 1603 sobre la obra de Johannes de Sacrobosco, y en la década de 1640, el polímata francés Marin Mersenne publicó grandes (¡pero no del todo correctas) tablas de factoriales, ¡hasta 64!, basadas en la obra de Clavius.[13] La serie de potencias para la función exponencial, con los recíprocos de factoriales para sus coeficientes, fue formulada por primera vez en 1676 por Isaac Newton en una carta a Gottfried Wilhelm Leibniz.[14] Otras obras importantes de las primeras matemáticas europeas sobre factoriales incluyen una amplia cobertura en un tratado de 1685 por John Wallis, un estudio de sus valores aproximados para grandes valores de por Abraham de Moivre en 1721, una carta de 1729 de James Stirling a de Moivre en la que se enunciaba lo que se conoció como aproximación de Stirling, y el trabajo en la misma época de Daniel Bernoulli y Leonhard Euler formulando la extensión continua de la función factorial a la función gamma.[15] Adrien-Marie Legendre incluyó la fórmula de Legendre, que describe los exponentes en la factorización de factoriales en potencias primos, en un texto de 1808 sobre teoría de números.[16]
La notación para los factoriales fue introducida por el matemático francés Christian Kramp en 1808.[17] También se han utilizado muchas otras notaciones. Otra notación posterior, en la que el argumento del factorial estaba semicerrado por los lados izquierdo e inferior de una caja, fue popular durante algún tiempo en Gran Bretaña y América, pero cayó en desuso, tal vez porque es difícil de tipografiar.[17] La palabra "factorial" (originalmente en francés: factorielle) fue utilizada por primera vez en 1800 por Louis François Antoine Arbogast,[18] en el primer trabajo sobre la fórmula de Faà di Bruno,[19] sino que se refiere a un concepto más general de productos de progresión aritméticas. Los "factores" a los que se refiere este nombre son los términos de la fórmula del producto para el factorial.[20]
Definición por producto e inducción
Podemos definir el factorial de un número entero positivo n, expresado n!, como el producto de todos los números enteros positivos menores o iguales que n.
- .
La multiplicación anterior también se puede representar utilizando el operador productorio:
- .
También es posible definirlo mediante la relación de recurrencia
En esta segunda definición el dominio de la función es el conjunto de los enteros no negativos ℤ≥0 y el codominio es el conjunto de los enteros positivos ℤ+.[21] En este caso hay una sucesión recurrente, el cálculo sucesivo de sus elementos se llama proceso recurrente y la igualdad n! = (n - 1)!n se nombra ecuación recurrente.[22]
La segunda definición incorpora la premisa de que
Cero factorial
Una extensión común, sin embargo, es la definición de factorial de cero. De acuerdo con la convención matemática de producto vacío, el valor de 0! debe definirse como:
Es posible, sin embargo, dar un argumento intuitivo para justificar la elección, como sigue:
- Para cada número entero positivo n mayor o igual que 1, es posible determinar el valor del factorial anterior mediante el uso de la siguiente identidad:
válida para todo número mayor o igual que 1.
Así, si se conoce que 5! es 120, entonces 4! es 24 porque
y por tanto 3! debe ser necesariamente 6 puesto que
El mismo proceso justifica el valor de 2! = 2 y 1! = 1 ya que:
Si aplicamos la misma regla para el caso en que n = 1 tendríamos que 0! corresponde a:
Aunque el argumento puede resultar algo convincente, es importante tener en cuenta que no es más que un argumento informal y que la razón real por la cual se toma la convención de 0! = 1 es por ser un caso especial de la convención de producto vacío usada en muchas otras ramas de las matemáticas.
Propiedades
- Si m y n son enteros positivos y m < n implica que m! < n!
- Si m < n resulta que m! es factor o divisor los cuales .. de n! y se tiene: n! = n(n-1)...(m+1).m! (1)
- El número n(n-1)...(m+1) es el producto de los n-m factores expuestos mayores de n!
- n-m es menor que n y reemplazando en (1) se obtiene n! = n(n-1)...(n-m+1).(n-m)![23]
- , para n> 1. Se aplica propiedad de que la media geométrica de los primeros enteros positivos no excede a la media aritmética de ellos.
Aplicaciones
Los factoriales se usan mucho en la rama de la matemática llamada combinatoria, a través del binomio de Newton, que da los coeficientes de la forma desarrollada de (a + b)n:
donde representa un coeficiente binomial:
De igual forma se puede encontrar en la derivación por la regla del producto para derivadas de orden superior de manera similar que el binomio de newton:
Donde f(n) es la derivada enésima de la función f.
Por medio de la combinatoria, los factoriales intervienen en el cálculo de las probabilidades. Intervienen también en el ámbito del análisis, en particular a través del desarrollo polinomial de las funciones (fórmula de Taylor). Se generalizan a los reales con la función gamma, de gran importancia en la teoría de números.
Para valores grandes de n, existe una expresión aproximada para el factorial de n, dado por la fórmula de Stirling:
La ventaja de esta fórmula es que no precisa inducción y, por lo tanto, permite evaluar n! más rápidamente cuando mayor sea n.
Extensión
La definición indicada de factorial es válida para números no negativos. Es posible extender la definición a otros contextos introduciendo conceptos más sofisticados, en especial es posible definirla para cualquier número real excepto para los números enteros negativos y para cualquier número complejo exceptuando de nuevo los números enteros negativos. El factorial de n es generalizado para cualquier número real n por la función gamma de manera que
solo para n > 0. Se puede generalizar aún más, para todo número complejo z que no sea igual a un entero no positivo, mediante la siguiente definición:
Productos similares
Primorial
El primorial (sucesión A002110 en OEIS) se define de forma similar al factorial, pero solo se toma el producto de los números primos menores o iguales que n:
- .
Doble factorial
Se define el doble factorial de n mediante la relación de recurrencia:
Por ejemplo:
La sucesión de dobles factoriales (sucesión A006882 en OEIS) para:
Empieza así:
La definición anterior puede extenderse para definir el doble factorial de números negativos:
Y esta es la sucesión de dobles factoriales para:
El doble factorial de un número negativo par no está definido.
Algunas identidades de los dobles factoriales:
Véase también
Referencias y citas
- Higgins, Peter (2008), Number Story: From Counting to Cryptography, New York: Copernicus, p. 12, ISBN 978-1-84800-000-1.
- Datta, Bibhutibhusan; Singh, Awadhesh Narayan (2019). Springer Singapore, Aditya; Mahesh, K., eds. Studies in Indian Mathematics and Astronomy: Artículos seleccionados de Kripa Shankar Shukla. Fuentes y Estudios en la Historia de las Matemáticas y las Ciencias Físicas. pp. 356-376. S2CID 191141516.
|editor1-last=y|editor=redundantes (ayuda). Revisado por K. S. Shukla a partir de un artículo publicado en Indian Journal of History of Science 27 (3): 231-249, 1992, MR 1189487. Véase p. 363. - Jadhav, Dipak (August 2021). «Jaina Thoughts on Unity Not Being a Number». History of Science in South Asia (University of Alberta Libraries) 9: 209-231. S2CID 238656716. doi:10.18732/hssa67.. Véase la discusión de la datación en la p. 211.
- Biggs, Norman L. (Mayo 1979). «Las raíces de la combinatoria». Historia Mathematica 6 (2): 109-136. MR 0530622. doi:10.1016/0315-0860(79)90074-0.
- Katz, Victor J. (June 1994). «Ethnomathematics in the classroom». Para el Aprendizaje de las Matemáticas 14 (2): 26-30. JSTOR 40248112.
- Sefer Yetzirah en Wikisource, Capítulo IV, Sección 4
- Rashed, Roshdi (1980). «Ibn al-Haytham et le théorème de Wilson». Archivo de Historia de las Ciencias Exactas (en francés) 22 (4): 305-321. MR 595903. S2CID 120885025.
- Acerbi, F. (2003). «On the shoulders of Hipparchus: a reappraisal of ancient Greek combinatorics». Archivo de Historia de las Ciencias Exactas 57 (6): 465-502. JSTOR 41134173. MR 2004966. S2CID 122758966. doi:10.1007/s00407-003-0067-0.
- Katz, Victor J. (2013). «Capítulo 4: Combinatoria judía». En Wilson, Robin; Watkins, John J., eds. Combinatoria: Ancient & Modern. Oxford University Press. pp. 109-121. ISBN 978-0-19-965659-2.
- Hunt, Katherine (May 2018). «The Art of Changes: Bell-Ringing, Anagrams, and the Culture of Combination in Seventeenth-Century England». Journal of Medieval and Early Modern Studies 48 (2): 387-412. doi:10.1215/10829636-4403136.
- Stedman, Fabian (1677). Campanalogia. London. pp. 6-9.} El editor aparece como "W.S.", que puede haber sido William Smith, posiblemente actuando como agente de la Sociedad de Jóvenes Universitarios, a cuya sociedad va dirigida la "Dedicatoria".
- Knobloch, Eberhard (2013). «Capítulo 5: Combinatoria del Renacimiento». En Wilson, Robin; Watkins, John J., eds. Combinatoria: Ancient & Modern. Oxford University Press. pp. 123-145. ISBN 978-0-19-965659-2. Véase p. 126.
- Knobloch, 2013.
- Ebbinghaus, H.-D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1990). id=Z53SBwAAQBAJ&pg=PA131 Numbers. Graduate Texts in Mathematics 123. New York: Springer-Verlag. p. 131. ISBN 0-387-97202-1. MR 1066206. doi:10.1007/978-1-4612-1005-4.
- Dutka, Jacques (1991). «La historia temprana de la función factorial». Archivo de Historia de las Ciencias Exactas 43 (3): 225-249. JSTOR 41133918. S2CID 122237769. doi:10.1007/BF00389433.
- Dickson, Leonard E. (1919). «Capítulo IX: Divisibilidad de factoriales y coeficientes multinomiales». Historia de la Teoría de Números 1. Institución Carnegie de Washington. pp. 263-278. Véase en particular la pág. 263.
- Cajori, Florian (1929). «448-449. Factorial "n"». A History of Mathematical Notations, Volume II: Notations Mainly in Higher Mathematics. The Open Court Publishing Company. pp. 71-77.
- Miller, Jeff. st-andrews.ac.uk/Miller/mathword/f/ «Usos más tempranos conocidos de algunas de las palabras de Matemáticas (F)». MacTutor History of Mathematics archive. University of St Andrews.
- Craik, Alex D. D. (2005). «Prehistoria de la fórmula de Faà di Bruno». The American Mathematical Monthly 112 (2): 119-130. JSTOR 30037410. MR 2121322. S2CID 45380805. doi:10.1080/00029890.2005.11920176.
- Arbogast, Louis François Antoine (1800). Du calcul des dérivations (en francés). Strasbourg: L'imprimerie de Levrault, frères. pp. 364-365.
- «Sucesiones recurrentes» de A. I. Markushévich, Editorial Progreso, 1998
- Fuente ut supra
- A. Adrián Albert: Álgebra superior, UTEHA, México /1991
Enlaces externos
 Wikilibros alberga un libro o manual sobre Implementaciones del factorial de un número.
Wikilibros alberga un libro o manual sobre Implementaciones del factorial de un número.- Calcular factorial de un número en PHP.
- Algoritmos interesantes(en inglés)
- http://factorielle.free.fr
- Calculadora de factoriales - Hasta 200.000