Grupo puntual

En geometría y cristalografía, un grupo puntual es un grupo de simetrías geométricas (grupo de isometría) que mantiene constante por lo menos un punto fijo. Los grupos puntuales pueden existir en un espacio euclidiano de cualquier otra dimensión, y cada grupo puntual en la dimensión d es un subgrupo del grupo ortogonal O(d). Los grupos puntuales pueden ser considerados como un conjunto de matrices ortogonales M que transforman un punto x en un punto y:

La flor Bauhinia blakeana representada en la bandera de Hong Kong tiene simetría C₅; la estrella interior de cada pétalo tiene simetría D₅.

y= M.x

donde el origen es el punto fijo. Los elementos de los grupos puntuales pueden ser: rotaciones (determinante de M= 1) rotaciones impropias, reflexiones, rotaciones-reflexiones, o rotoreflexiones (determinante de M= -1). Todos los grupos puntuales de las rotaciones de dimensión d son subgrupos del grupo ortogonal especial SO(d).

Los grupos puntuales discretos en más de una dimensión se agrupan en familias infinitas, pero por el teorema de restricción cristalográfica y por uno de los teoremas de Bieberbach, cada número de dimensiones solo tiene un número finito de grupos puntuales que son simétricos respecto de una red o retícula con ese número de dimensiones. Estos son los grupos puntuales cristalográficos.

Una dimensión

Solo hay dos grupos puntuales unidimensionales, el grupo identidad y el grupo reflexión.

Grupo	Coxeter	Diagrama de Coxeter	Orden	Descripción
C₁	[ ]⁺		1	Identidad
D₁	[ ]		2	Grupo reflexión

Dos dimensiones

Los grupos puntuales planos son a veces llamados grupos de roseta.

Se agrupan en dos familias infinitas:

Grupos cíclicos C_n o grupos de rotación de orden n
Grupos diedral D_n de rotación de orden n y grupos de reflexión.

Aplicando el teorema de restricción cristalográfica n queda limitado a los valores 1, 2, 3, 4 y 6 para ambas familias, produciendo 10 grupos.

Grupo	Intl	Orbifold	Coxeter	Orden	Descripción
C_n	n	nn	[n]⁺	n	Cíclico: rotaciones de orden n. Extraer el grupo Z_n, el grupo de los enteros bajo la adición módulo n.
D_n	nm	*nn	[n]	2n	Diedral: cíclico con reflexiones. Extraer el grupo Dih_n, el grupo diedral.

El subconjunto de grupos puntuales de reflexión pura, se define por uno o dos ejes de simetría, también se puede dar por su grupo de Coxeter y polígonos relacionados. Estos incluyen cinco grupos cristalográficos.

Grup0	Coxeter group		Orden	Polígonos relacionados
D₃	A₂	[3]	6	Triángulo equilátero
D₄	BC₂	[4]	8	Cuadrado
D₅	H₂	[5]	10	Pentágono regular
D₆	G₂	[6]	12	Hexágono regular
D_n	I₂(n)	[n]	2n	Polígono regular
D_2n	I₂(2n)	[[n]]=[2n]	4n	Polígono regular
D₂	A₁²	[2]	4	Rectángulo
D₁	A₁	[ ]	2	Dígono

Tres dimensiones

Los grupos puntuales tridimensionales son a veces llamados grupos puntuales moleculares por su amplio uso en el estudio de las simetrías de las moléculas pequeñas.

Se agrupan en siete familias infinitas de grupos axiales o prismáticos, y 7 grupos poliédricos adicionales o grupos platónicos. En notación de Schönflies,

Los grupos axiales: C_n, S_2n, C_nh, C_nv, D_n, D_nd, D_nh
Grupos poliédricos: T, T_d, T_h, O, O_h, I, I_h

Aplicando el teorema de restricción cristalográfica a estos grupos se obtienen los 32 grupos puntuales cristalográficos.

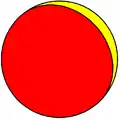
Dominios cuyo grupo de simetría se corresponde con los grupos puntuales
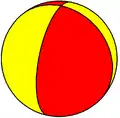
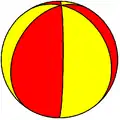
C_1v Orden 2	C_2v Orden 4	C_3v Orden 6	C_4v Orden 8	C_5v Orden 10	C_6v Orden 12	...

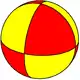
D_1h Orden 4	D_2h Orden 8	D_3v Orden 12	D_4h Orden 16	D_5h Orden 20	D_6h Orden 24	...

T_d Orden 24	O_h Orden 48	I_h Orden 120

Intl^*	Geo [1]	Orbifold	Schönflies	Conway	Coxeter	Orden
1	1	1	C₁	C₁	[ ]⁺	1
1	22	×1	C_i = S₂	CC₂	[2⁺,2⁺]	2
2 = m	1	*1	C_s = C_1v = C_1h	±C₁ = CD₂	[ ]	2
2 3 4 5 6 n	2 3 4 5 6 n	22 33 44 55 66 nn	C₂ C₃ C₄ C₅ C₆ C_n	C₂ C₃ C₄ C₅ C₆ C_n	[2]⁺ [3]⁺ [4]⁺ [5]⁺ [6]⁺ [n]⁺	2 3 4 5 6 n
2mm 3m 4mm 5m 6mm nmm nm	2 3 4 5 6 n	22 33 44 55 66 nn	C_2v C_3v C_4v C_5v C_6v C_nv	CD₄ CD₆ CD₈ CD₁₀ CD₁₂ CD_2n	[2] [3] [4] [5] [6] [n]	4 6 8 10 12 2n
2/m 3/m 4/m 5/m 6/m n/m	2 2 3 2 4 2 5 2 6 2 n 2	2* 3* 4* 5* 6* n*	C_2h C_3h C_4h C_5h C_6h C_nh	±C₂ CC₆ ±C₄ CC₁₀ ±C₆ ±C_n / CC_2n	[2,2⁺] [2,3⁺] [2,4⁺] [2,5⁺] [2,6⁺] [2,n⁺]	4 6 8 10 12 2n
4 3 8 5 12 2n n	4 2 6 2 8 2 10 2 12 2 2n 2	2× 3× 4× 5× 6× n×	S₄ S₆ S₈ S₁₀ S₁₂ S_2n	CC₄ ±C₃ CC₈ ±C₅ CC₁₂ CC_2n / ±C_n	[2⁺,4⁺] [2⁺,6⁺] [2⁺,8⁺] [2⁺,10⁺] [2⁺,12⁺] [2⁺,2n⁺]	4 6 8 10 12 2n

Intl^*	Geo [1]	Orbifold	Schönflies	Conway	Coxeter	Orden
222 32 422 52 622 n22 n2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22n	D₂ D₃ D₄ D₅ D₆ D_n	D₄ D₆ D₈ D₁₀ D₁₂ D_2n	[2,2]⁺ [2,3]⁺ [2,4]⁺ [2,5]⁺ [2,6]⁺ [2,n]⁺	4 6 8 10 12 2n
mmm 6m2 4/mmm 10m2 6/mmm n/mmm 2nm2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22n	D_2h D_3h D_4h D_5h D_6h D_nh	±D₄ DD₁₂ ±D₈ DD₂₀ ±D₁₂ ±D_2n / DD_4n	[2,2] [2,3] [2,4] [2,5] [2,6] [2,n]	8 12 16 20 24 4n
42m 3m 82m 5m 122m 2n2m nm	4 2 6 2 8 2 10 2 12 2 n 2	22 23 24 25 26 2n	D_2d D_3d D_4d D_5d D_6d D_nd	±D₄ ±D₆ DD₁₆ ±D₁₀ DD₂₄ DD_4n / ±D_2n	[2⁺,4] [2⁺,6] [2⁺,8] [2⁺,10] [2⁺,12] [2⁺,2n]	8 12 16 20 24 4n
23	3 3	332	T	T	[3,3]⁺	12
m3	4 3	3*2	T_h	±T	[3⁺,4]	24
43m	3 3	*332	T_d	TO	[3,3]	24
432	4 3	432	O	O	[3,4]⁺	24
m3m	4 3	*432	O_h	±O	[3,4]	48
532	5 3	532	I	I	[3,5]⁺	60
53m	5 3	*532	I_h	±I	[3,5]	120

(*) Cuando el símbolo en la columna Intl aparece duplicado, el primero es para n par, el segundo para n impar.

El subconjunto de grupos puntuales de reflexión pura, definido por 1 a 3 planos de simetría, también se puede dar por su grupo de Coxeter y poliedros relacionados. El grupo [3,3] se puede doblar, notándose como [[3,3]], haciendo coincidir los ejes primero y último uno sobre el otro, duplicando la simetría a orden 48, y resultando isomorfo con el grupo [4,3].

Schönflies	Grupo de Coxeter		Orden	Poliedro regular y prismático relacionado
T_d	A₃	[3,3]	24	Tetraedro
O_h	BC₃	[4,3] =[[3,3]]	48	Cubo, octaedro Octaedro estrellado
I_h	H₃	[5,3]	120	Icosaedro, dodecaedro
D_3h	A₂×A₁	[3,2]	12	Prisma triangular
D_4h	BC₂×A₁	[4,2]	16	Prisma cuadrado
D_5h	H₂×A₁	[5,2]	20	Prisma pentagonal
D_6h	G₂×A₁	[6,2]	24	Prisma hexagonal
D_nh	I₂(n)×A₁	[n,2]	4n	Prisma n-gonal
D_2h	A₁³	[2,2]	8	Cuboide
C_3v	A₂×A₁	[3]	6	Hosoedro
C_4v	BC₂×A₁	[4]	8
C_5v	H₂×A₁	[5]	10
C_6v	G₂×A₁	[6]	12
C_nv	I₂(n)×A₁	[n]	2n
C_2v	A₁²	[2]	4
C_s	A₁	[ ]	2

Véase también

Grupos puntuales bidimensionales
Grupos puntuales tridimensionales
Cristalografía
Grupo puntual cristalográfico
Simetría molecular
Grupo espacial
Difracción de rayos X
Red de Bravais

Notas

The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF Archivado el 20 de octubre de 2020 en Wayback Machine.

Referencias

Los grupos puntuales. En: Teoría de grupos aplicada para químicos, físicos e ingenieros. Allen Nussbaum. Editorial Reverté, 1975. ISBN 842914109X.
H.S.M. Coxeter: Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
H.S.M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980
N.W. Johnson: Geometries and Transformations, Manuscript, (2011) Chapter 11: Finite symmetry groups

Enlaces externos

Tutorial sobre grupos puntuales (necesita Java y Flash)
Lista de subgrupos (necesita Java)
The Geometry Center: 2.1 Formulas for Symmetries in Cartesian Coordinates (two dimensions)
The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions)

Datos: Q899720
Multimedia: Point groups / Q899720

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[HH-1] The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF Archivado el 20 de octubre de 2020 en Wayback Machine.