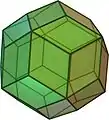
Hexecontaedro deltoidal

Las 60 caras son deltoides (también denominados cometas). Los bordes corto y largo de cada deltoide están en la proporción 1:7 + √5/6 ≈ 1:1.539344663...

El ángulo entre dos aristas cortas en una sola cara es arccos(-5-2√5/20)≈118.2686774705°. El ángulo opuesto, entre los bordes largos, es arccos(-5+9√5/40)≈67.783011547435°. Los otros dos ángulos de cada cara, entre un lado corto y uno largo, son ambos iguales a arccos(5-2√5/10)≈86.97415549104°.

El ángulo diedro entre cualquier par de caras adyacentes es arccos(-19-8√5/41)≈154.12136312578°.

Topológicamente, el hexecontaedro deltoidal es idéntico al hexecontahedro rómbico no convexo. El hexecontaedro deltoidal se puede derivar de un dodecaedro (o icosaedro) desplazando los centros de las caras, los centros de las aristas y los vértices hacia diferentes radios del centro del cuerpo. Los radios se eligen de modo que la forma resultante tenga caras planas de cometa, cada una de manera que los vértices vayan a las esquinas de grado 3, las caras a las esquinas de grado cinco y los centros de las aristas a los puntos de grado cuatro.

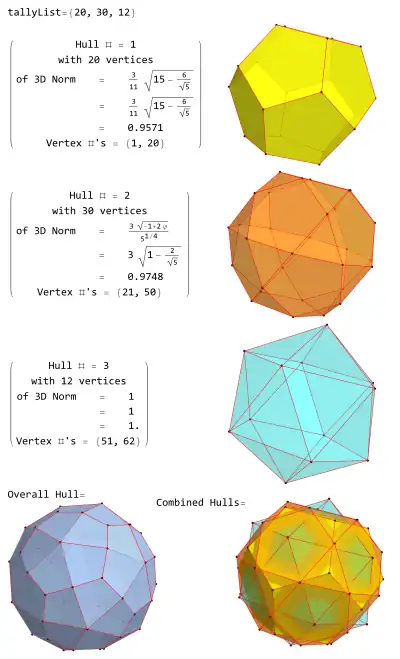
Los 62 vértices del disdiaquis triacontaedro caen en tres conjuntos centrados en el origen:

• Veinte vértices tienen la forma de un dodecaedro regular escalado por ${\displaystyle {\frac {3}{11}}{\sqrt {15-{\frac {6}{\sqrt {5}}}}}\approx 0.9571}$.
• Treinta vértices tienen la forma de un icosidodecaedro escalado por ${\displaystyle 3{\sqrt {1-{\frac {2}{\sqrt {5}}}}}\approx 0.9748}$.
• Doce vértices pertenecen a un icosaedro regular inscrito en una esfera unidad.

Estos tres poliedros se visualizan en las siguientes figuras:

El hexecontaedro deltoidal tiene 3 posiciones de simetría ubicadas en los 3 tipos de vértices:

Proyecciones ortogonales

Simetría proyectiva	[2]	[2]	[2]	[2]	[6]	[10]
Imagen
Imagen dual

Esta figura, procedente de la obra Perspectiva Corporum Regularium (1568) de Wenzel Jamnitzer puede verse como un hexecontaedro deltoidal

El hexecontaedro deltoidal se puede construir a partir de un icosaedro regular o de un dodecaedro regular agregando vértices en la mitad de cada arista y en la mitad de cada cara, y creando nuevas aristas desde el centro de cada arista hasta los centros de las caras. La notación de poliedros de Conway los daría como oI y oD, orto-icosaedro y orto-dodecaedro. Estas variaciones geométricas existen como un continuo en un grado de libertad.

Hexecontaedro deltoidal esférico

Familia de poliedros icosaédricos uniformes
Simetría: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duales de los poliedros uniformes
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Cuando se proyecta sobre una esfera (véase a la derecha), se puede observar que las aristas forman las aristas de un icosaedro y de un dodecaedro dispuestas en sus posiciones duales (equivalente al compuesto de dodecaedro e icosaedro).

Este teselado está relacionado topológicamente como parte de la secuencia de poliedros deltoidales con figura de cara (V3.4.n.4), y continúa con teselados del plano hiperbólico. Estas figuras isoedrales tienen simetría reflexiva (*n32).

* Simetría n32; mutación de teselados expandidos duales: V3.4.n.4

Simetría *n32 [n,3]	Esférica				Euclídea	Hiperb. compacta		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figura config. vértices	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

• Sólidos de Catalan
• Poliedro dual
• Poliedros
• Poliedro de caras uniformes
• Truncamiento (geometría)
• Icositetraedro deltoidal

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Sección 3-9)
• Las simetrías de las cosas 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 asp?ProdCode=2205 (Capítulo 21, Nomenclatura de los poliedros y mosaicos de Arquímedes y Catalanes, página 286, hexecontaedro tetragonal)
• http://mathworld.wolfram.com/ArchimedeanDualGraph.html

• Weisstein, Eric W. «DeltoidalHexecontahedron and Hamiltonian path». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
• Deltoidal Hexecontahedron (Trapezoidal Hexecontrahedron)—Modelo de poliedro interactivo
• Ejemplo en la vida real—Una pelota de casi 4 metros de de diámetro, de nilón ripstop, e inflado por el viento. Rebota en el suelo para que los niños puedan jugar con él en los festivales de cometas.