Método AXE
En química, el método AXE o método ABE es comúnmente usado para encontrar la geometría de las moléculas siguiendo la teoría VSEPR.[1] Este método permite determinar la estructura molecular indicando el número de átomos centrales, átomos sustituyentes periféricos y pares de electrones no compartidos.
Aplicación
La A representa el átomo central y siempre tiene un subíndice implícito igual a uno. La X o la B representa el número de enlaces sigma entre el átomo central y los átomos exteriores. Los enlaces covalentes múltiples solo cuentan como una X. La E representa el número de pares de electrones solitarios que rodean el átomo central. La suma de X y E, conocida como número estérico, también se asocia con el número total de orbitales híbridos utilizado por la teoría del enlace de valencia.
Con base en el número estérico y la distribución de los valores de X y E, la teoría RPECV hace unas predicciones de geometría molecular, según se muestra en las siguientes tablas.[2] Téngase en cuenta que las geometrías se nombran de acuerdo a las posiciones de los átomos y no de la disposición de los electrones. Por ejemplo, la descripción de AX2E1 como angular indica que la molécula AX2 es una molécula angular sin hacer referencia al par (o pares) solitario de electrones, aunque ese par sí influye en la geometría observada.
Tipos de moléculas con átomo central (notación AXE)
| Nº estérico |
Geometría básica 0 pares solitarios |
1 par solitario | 2 pares solitarios | 3 pares solitarios |
|---|---|---|---|---|
| 2 | ||||
| 3 | 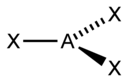 | 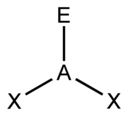 | ||
| 4 | 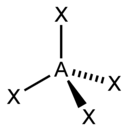 |  |  | |
| 5 | 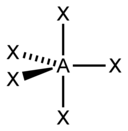 |  |  | 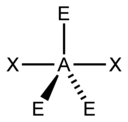 |
| 6 |  | 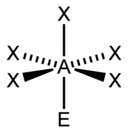 | 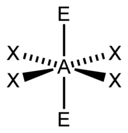 | |
| 7 | 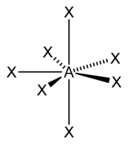 | 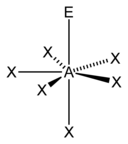 | ||
| 8 |
Tipos de moléculas y ejemplos (notación AXE)
| Tipo de molécula | Forma | Distribución electrónica† | Geometría‡ | Ejemplos |
|---|---|---|---|---|
| AX1En | Diatómica | HF, O2 | ||
| AX2E0 | Lineal | BeCl2, HgCl2, CO2 | ||
| AX2E1 | Angular |  |
 |
NO2−, SO2, O3 |
| AX2E2 | Angular |  |
 |
H2O, OF2 |
| AX2E3 | Lineal |  |
XeF2, I3− | |
| AX3E0 | Trigonal plana |  |
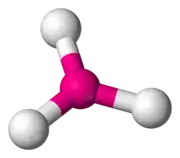 |
BF3, CO32−, NO3−, SO3 |
| AX3E1 | Piramidal trigonal |  |
 |
NH3, PCl3 |
| AX3E2 | Forma de T |  |
 |
ClF3, BrF3 |
| AX4E0 | Tetraédrica |  |
 |
CH4, PO43−, SO42−, ClO4− |
| AX4E1 | Balancín |  |
 |
SF4 |
| AX4E2 | Cuadrada plana |  |
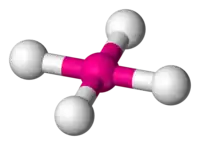 |
XeF4 |
| AX5E0 | Bipiramidal trigonal |  |
 |
PCl5 |
| AX5E1 | Piramidal cuadrada |  |
 |
ClF5, BrF5 |
| AX6E0 | Octaédrica |  |
 |
SF6 |
| AX6E1 | Piramidal pentagonal |  |
 |
XeOF5−, IOF52−[3] |
| AX7E0 | Bipiramidal pentagonal | 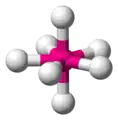 |
 |
IF7 |
| AX8E0 | Antiprisma cuadrado Dodecaédrica D2d |
XeF82− Mo(CN)84− | ||
| AX9E0 | Prismática trigonal triapuntada | ReH92−]] | ||
| AX10E0 | Antiprisma tetragonal biapuntado | [U(CH3CO2)4]n | ||
| AX12E0 | Icosaédrica | Pr(C8H6N2)63+c |
Cuando los átomos sustituyentes (X) no son todos iguales, la geometría es todavía aproximadamente válida, pero los ángulos de enlace pueden ser ligeramente diferentes a los de aquellos casos en los que todos los átomos exteriores son los mismos. Por ejemplo, los carbonos unidos por doble enlace en los alquenos como el C2H4 son del tipo AX3E0, pero los ángulos de enlace no son exactamente 120°. Del mismo modo, el SOCl2 es del tipo AX3E1, y debido a que los sustituyentes X no son idénticos, los ángulos X-A-X no son todos iguales.
Como una herramienta para predecir la geometría adoptada con un número determinado de pares de electrones, una demostración física de uso frecuente del principio de repulsión electrostática mínima utiliza globos inflados. Mediante frotamiento, los globos adquieren una carga electrostática superficial leve que se traduce en la adopción de geometrías más o menos similares cuando están unidos por sus boquillas que el correspondiente número de pares de electrones. Por ejemplo, cinco globos atados adoptan la geometría de bipirámide trigonal tal como lo hacen los enlaces de una molécula de PCl5 (AX5) o los dos pares enlazantes y tres pares no enlazantes de una molécula de XeF2 (AX2E3). La geometría molecular de la primera es también bipiramidal trigonal, mientras que la de este último es lineal.
Véase también
 Wikimedia Commons alberga una categoría multimedia sobre Método AXE.
Wikimedia Commons alberga una categoría multimedia sobre Método AXE.- Teoría RPECV
- Geometría molecular
Enlaces externos
- Cap. 6: Estructura molecular y Estereoquímica: especies covalentes sencillas. En: Química inorgánica: texto superior para uso de los estudiantes de las facultades de ciencias y escuelas de ingeniería. Therald Moeller. Editorial Reverté, 1994. ISBN 8429173900. Pág. 295
- Molecular geometry. Barron's how to prepare for the AP chemistry advanced placement examination. Neil D. Jespersen. Barron's Educational Series, 2003. ISBN 0764120220. Pág. 111
- Molecular origami: precision scale models from paper. Robert M. Hanson. University Science Books, 1995. ISBN 093570230X.
Referencias
- Chemistry Quick Study Guide Archivado el 10 de agosto de 2014 en Wayback Machine.. Mobile Reference, 2007. ISBN 160501107X. Pág. 242
- Forma de las moléculas y orbitales híbridos. En: Química. Ronald J. Gillespie, Aurelio Beltrán. Editorial Reverté, 1988. ISBN 8429171886. Pág. 1070
- Baran, E. (2000). «Mean amplitudes of vibration of the pentagonal pyramidal XeOF5− and IOF52− anions». Journal of Fluorine Chemistry (en inglés) 101: 61-63. doi:10.1016/S0022-1139(99)00194-3.
- General chemistry: principles and structure. James E. Brady, Gerard E. Humiston. Wiley, 1975. ISBN 0471095303.