Teoría cuántica de campos
La teoría cuántica de campos es una disciplina de la física que aplica los principios de la mecánica cuántica a los sistemas clásicos de campos continuos, por ejemplo, el campo electromagnético. Una consecuencia inmediata de esta teoría es que el comportamiento cuántico de un campo continuo es equivalente al de un sistema de partículas[n 1] cuyo número no es constante, es decir, que pueden crearse o destruirse.[1] También se la denomina teoría de campos cuánticos, TCC[n 2] o QFT, sigla en inglés de quantum field theory.
Su principal aplicación es la física de altas energías, donde se combina con los postulados de la relatividad especial. En este régimen se usa para estudiar las partículas subatómicas y sus interacciones, y permite explicar fenómenos como la relación entre espín y estadística, la simetría CPT, la existencia de antimateria, etc.[2]
También es una herramienta habitual en el campo de la física de la materia condensada, donde se utiliza para describir las excitaciones colectivas de sistemas de muchas partículas y entender efectos físicos tales como la superconductividad, la superfluidez o el efecto Hall cuántico.[3]
En particular, la teoría cuántica del campo electromagnético, conocida como electrodinámica cuántica, fue el primer ejemplo de teoría cuántica de campos que se estudió y es la teoría física probada experimentalmente con mayor precisión.[4] Los fundamentos de la teoría de campos cuántica fueron desarrollados entre las décadas de 1920 y 1950 por Dirac, Fock, Pauli, Tomonaga, Schwinger, Feynman y Dyson, entre otros.
Historia



El desarrollo de la teoría cuántica de campos ocurrió simultáneamente con el de la mecánica cuántica «ordinaria», en un intento de explicar los fenómenos atómicos tomando también en cuenta las leyes de la teoría de la relatividad.[5] Entre 1926 y 1928 se desarrollaron los primeros intentos de encontrar una ecuación de onda relativista que describiera el movimiento de una partícula cuántica, debidos a Erwin Schrödinger y a Paul Dirac. Sin embargo, dichas ecuaciones mostraban ciertas inconsistencias.
Por otro lado, en 1926 Werner Heisenberg, Pascual Jordan y Max Born profundizaron en el estudio del problema del cuerpo negro: el comportamiento de la radiación electromagnética dentro de una cavidad, en ausencia de partículas cargadas. Esto constituyó el primer ejemplo de una teoría cuántica de campos, en este caso aplicando las reglas de cuantización al campo electromagnético. En sus resultados, la radiación se comportaba como un conjunto de partículas —los fotones—, en consonancia con la hipótesis de los cuantos de luz, formulada por Einstein en 1905. Tras este ejemplo, las mencionadas ecuaciones de onda relativistas se estudiaron de nuevo desde otro punto de vista. En lugar de interpretarlas como funciones de onda, se usaron las reglas de cuantización de un campo clásico para manipularlas. De este modo se obtuvieron ecuaciones para partículas cuánticas respetando las leyes de la relatividad que sí eran consistentes. Esta reinterpretación, conocida como segunda cuantización, fue llevada a cabo por Heisenberg, Wolfgang Pauli, Vladimir Fock, Wendell Furry, Robert Oppenheimer y Victor Weisskopf.
A pesar de sus éxitos iniciales, la teoría cuántica de campos tenía problemas teóricos muy serios. El cálculo de muchas cantidades físicas en apariencia ordinarias resultaba en un valor infinito, un resultado sin sentido. Un ejemplo de esto eran las pequeñas diferencias entre algunos niveles de energía en el átomo de hidrógeno, la llamada estructura fina. Este «problema de las divergencias» fue resuelto durante las décadas de 1930 y 1940 por Julian Schwinger, Freeman Dyson, Richard Feynman y Shin'ichiro Tomonaga entre otros, mediante una técnica conocida como renormalización. Esta etapa culminó con el desarrollo de la moderna electrodinámica cuántica —QED, por Quantum Electrodynamics—. La técnica de los diagramas de Feynman, un procedimiento gráfico de cálculo desarrollado por Richard Feynman, se convirtió en una de las herramientas básicas de la teoría cuántica de campos.
En la década de 1950 QED fue generalizada a una clase más general de teorías conocidas como teorías gauge, comenzando con el trabajo de Chen Ning Yang y Robert Mills.[6] A finales de la década de 1960, Sheldon Glashow, Abdus Salam y Steven Weinberg unificaron las interacciones electromagnética y débil en la teoría electrodébil —una teoría gauge— mediante el concepto de ruptura espontánea de simetría, introducido originariamente para explicar la superconductividad.[7]
Sin embargo, no fue hasta la década de 1970 que quedó establecido el modelo estándar de la física de partículas. El modelo de unificación electrodébil no recibió especial atención hasta que, en 1971, Gerardus 't Hooft y Martinus Veltman demostraron que las teorías con simetrías rotas espontáneamente podían ser renormalizadas.[8] Por otro lado, la intensidad de las interacciones fuertes entre hadrones fue un desafío para los teóricos de campos hasta el desarrollo del concepto de la libertad asintótica por Frank Wilczek, David Gross y Hugh David Politzer en 1973.[9]
También durante la década de 1970, la teoría cuántica de campos «rompió los grilletes de los diagramas de Feynman», al descubrirse que las soluciones no perturbativas de las ecuaciones de los campos clásicos juegan un papel crucial a nivel cuántico.[10] Además, la actitud hacia la técnica de la renormalización y hacia la teoría cuántica de campos en general fue cambiando progresivamente, gracias a los avances de —entre otros— Kenneth Wilson en física de la materia condensada. La aparición de los infinitos pasó de ser considerada una «patología» a «simplemente un recordatorio de una limitación práctica: no conocemos qué ocurre a distancias mucho más pequeñas que aquellas que podemos observar directamente».[11]
Principios básicos
Limitaciones en la mecánica cuántica
En mecánica cuántica «ordinaria», un conjunto de partículas se describe mediante una función de onda Ψ(r1, ..., rn), que recoge la probabilidad de encontrar a cada una de estas en un punto dado.[n 3] Además, la evolución en el tiempo de esta función de onda está dictada por la ecuación de Schrödinger:[n 4][12]
(1)
Sin embargo, este esquema no describe adecuadamente algunos aspectos que se encuentran en algunos sistemas físicos:
- Creación y destrucción
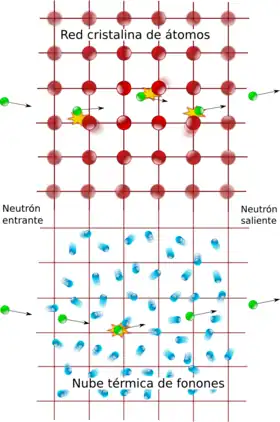
- Durante la evolución de este sistema, el número de partículas se mantiene finito e invariable —a saber, n—. Sin embargo, en experimentos de altas energías es corriente que el número de partículas varíe —por ejemplo en la desintegración de un neutrón, o la aniquilación de un electrón y un positrón en fotones—, como consecuencia de la famosa relación masa-energía de la relatividad. Además, en el contexto de física del estado sólido, las excitaciones de un colectivo de átomos se reinterpretan como cuasipartículas, como el fonón,[n 5] cuyo número es también variable.[1][13]
- Invariancia relativista
- Esta ecuación no refleja las propiedades de la cinemática relativista. Su límite clásico describe el movimiento de una partícula bajo las leyes de la mecánica galileana, en lugar de la mecánica relativista: el primer término de la izquierda en () se corresponde con la energía cinética no relativista p2/2m,[14] en lugar de la expresión relativista (p2 + m2)1/2, donde p es el momento de la partícula.[15]
- Campo clásico
- Las interacciones entre las n partículas del sistema tienen lugar mediante fuerzas a distancia, dadas por el potencial V. Sin embargo, en la física clásica existen sistemas más generales, que no pueden entenderse mediante este esquema. Es por ejemplo el caso de un conjunto de cargas eléctricas en movimiento: para describir su evolución es necesario tener en cuenta de forma independiente tanto las partículas cargadas como el campo electromagnético que generan.[14]
Es posible modificar la ecuación de Schrödinger para obtener una versión consistente con los principios de la relatividad especial, como la ecuación de Klein-Gordon o la ecuación de Dirac. Sin embargo, estas tienen muchas propiedades insatisfactorias: por ejemplo, predicen la existencia de partículas con energía negativa, de modo que el sistema resulta ser inestable.[16] Estos defectos son debidos a que dichas ecuaciones tampoco contemplan la posibilidad de que las partículas puedan crearse o destruirse y, como se menciona en el primer epígrafe, es inconsistente suponer una teoría relativista con un número constante de partículas en interacción.[1][13]
Definición
Una teoría cuántica de campos es el resultado de aplicar las reglas de cuantización al sistema de una teoría clásica de campos.[17] Esto permite estudiar los aspectos cuánticos de los campos continuos, como el campo electromagnético. Además, la cuantización de un campo presenta aspectos singulares: las reglas de cuantización aplicadas a un campo continuo revelan que sus posibles estados se corresponden con los de un colectivo de partículas idénticas que pueden crearse y destruirse. Por último, en el caso particular de que la ecuación del campo clásico respete la teoría de la relatividad, el sistema cuántico obtenido hereda esta propiedad. De este modo, la cuantización de un campo clásico sirve para cubrir los diversos aspectos que una teoría cuántica «ordinaria» no describe correctamente.
Segunda cuantización

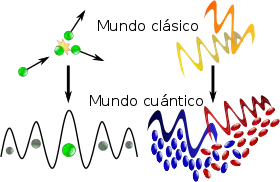
El proceso de aplicar las reglas de cuantización a un campo e identificar sus posibles estados cuánticos con los de un colectivo de partículas se denomina segunda cuantización.[n 6][18]
Límite continuo
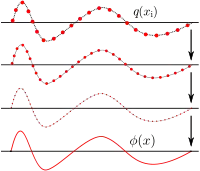
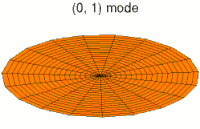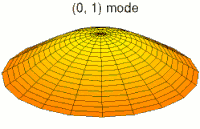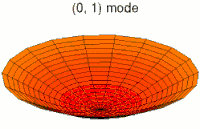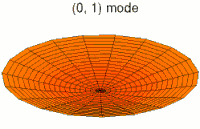
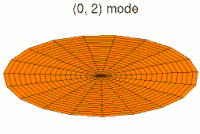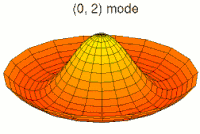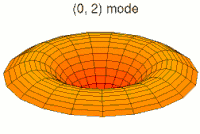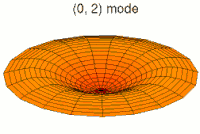
En mecánica clásica, un campo continuo es equivalente a un conjunto de múltiples osciladores acoplados entre sí. El ejemplo habitual para entender esta equivalencia es un sólido elástico. Este sistema puede describirse macroscópicamente mediante, por ejemplo, la densidad o la tensión en cada punto del mismo; cantidades que se representan mediante campos continuos. Por otro lado, también es posible describir el sólido como una red de partículas que ejercen fuerzas elásticas entre sí —como si estuvieran unidas por muelles imaginarios—, lo que conforma un sistema de osciladores acoplados. La primera descripción —el campo y sus ecuaciones— es una aproximación de la segunda —los osciladores— cuando se considera la separación media entre partículas muy pequeña, o dicho de otro modo, en el límite continuo.[19]
Esta equivalencia también se refleja en la evolución en el tiempo de estos sistemas. Visto como un conjunto de osciladores acoplados, las vibraciones (clásicas) de los átomos en el sólido son una superposición de sus modos normales: sus vibraciones colectivas elementales, o armónicos. Visto como un continuo de materia, las ondas de —por ejemplo— la densidad del sólido son una superposición de ondas planas, las ondas más simples. Cada modo normal o armónico del conjunto de osciladores se corresponde con una cierta onda plana del campo en el límite continuo.
| Osciladores acoplados | Límite continuo |
Campo continuo |
| Dinámica en términos de: |
Dinámica en términos de: | |
| Modos normales | Límite continuo |
Ondas planas |
Existen campos clásicos que no se corresponden con el límite clásico de ningún sistema mecánico, como por ejemplo el campo electromagnético. Sin embargo, la analogía matemática de sus ecuaciones con las de un sistema de osciladores abstractos sigue siendo válida.[20]
Osciladores cuánticos
La energía en un oscilador armónico cuántico está cuantizada, de modo que sólo puede ser un múltiplo de su frecuencia ω:[n 7]
donde ℏ es la constante reducida de Planck y N = 0, 1, 2, ... es un número entero no negativo. En un sistema de osciladores cuánticos acoplados la energía también es discreta, y es la suma de la energía de cada modo normal, visto como un oscilador independiente:
(2)
donde cada ωmodo i es la frecuencia de un modo normal y cada Nmodo i = 0, 1, 2, ... el nivel de excitación de dicho modo.
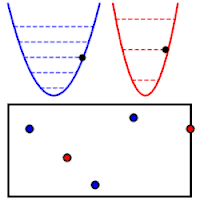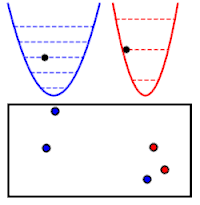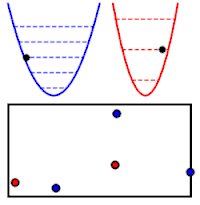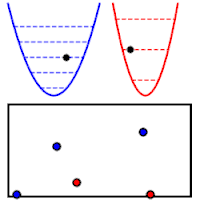
Sin embargo, estos valores son muy parecidos a los de un sistema de múltiples partículas repartidas por diversos niveles de energía E1, E2, etc. En este caso:
Estas dos expresiones para la energía son equivalentes, cuando se identifica cada nivel de energía con un modo normal y su frecuencia, ℏωmodo i = Enivel i; y la cantidad de partículas en un cierto nivel con el nivel de excitación del correspondiente modo normal, Nnivel i = Nmodo i. Por ejemplo, si Nmodo 5 = 2, el oscilador correspondiente al modo 5 está en su 2.º nivel de excitación, y tiene la misma energía que un sistema de dos partículas, cada una de ellas con energía Enivel 5 = ℏωmodo 5. Esta igualdad no se limita a una coincidencia en el valor de la energía: el comportamiento de ambos sistemas es muy parecido. Por lo tanto las propiedades físicas de un conjunto de osciladores cuánticos acoplados son iguales a las de un sistema de partículas cuánticas de número variable.
Campo cuántico
Un campo cuántico puede entenderse como el límite continuo de un conjunto de osciladores cuánticos acoplados. La energía de estos está dada por la ecuación (), por lo que la energía del campo tiene una forma análoga, haciendo referencia a las ondas planas del campo en lugar de a los modos normales. Por lo tanto, un campo cuántico constituye un sistema equivalente al de un conjunto de partículas de número variable.[21]
| Osciladores acoplados | Límite continuo |
Campo continuo |
| se cuantiza en |
se cuantiza en | |
| Osc. cuánticos acoplados | Límite continuo |
Campo cuántico |
Campo cuántico libre
La analogía entre osciladores y campo de la segunda cuantización se aplica directamente en el proceso de cuantización de un campo libre, aquel cuyas ecuaciones de campo son lineales. La equivalencia con un sistema de osciladores armónicos acoplados es exacta, y la energía del campo viene dada por la ecuación (): es la suma de la energía de cada partícula individual. Puesto que no hay contribuciones adicionales, las partículas son libres y no interaccionan entre sí, de ahí el nombre de campo libre.[22] Como consecuencia de la ausencia de interacción, el número de dichas partículas permanece constante.[23][n 8]
El estado de un campo cuántico se describe de manera habitual utilizando números de ocupación: el número de partículas en cada nivel de energía posible.[24] Por ejemplo: una partícula en el 1.er nivel, cero en el 2.º, dos en el 3.º, etc. Al estado sin ninguna partícula, en el que todos los niveles de energía están desocupados, se le denomina el vacío.[25]
Un aspecto importante de estas partículas es que son indistinguibles. Por ejemplo, si el estado del sistema consiste en una partícula en el 1.er nivel de energía y otra en el 2.º, intercambiarlas entre sí no da lugar a un estado distinto: se sigue teniendo una partícula en el nivel 1 y otra en el 2. Además, la analogía entre osciladores y campo conlleva que el número de ocupación de un cierto nivel de energía puede ser arbitrariamente alto, en particular mayor que 1. Esto significa que las partículas que surgen de la cuantización del campo son bosones.[26] La cuantización de un campo libre para obtener fermiones (u otros tipos de campos más complicados) requiere ciertas modificaciones en el método de segunda cuantización, pero el proceso y los resultados básicos son los mismos.[n 9]
Fermiones
Existen multitud de partículas llamadas fermiones —como el electrón y el protón— que respetan el principio de exclusión de Pauli, de modo que sus números de ocupación solo pueden valer 0 o 1. El formalismo de segunda cuantización basado en la analogía básica entre osciladores y campo no impone este límite y no es capaz de describir un conjunto de fermiones.[24]
El origen de la estadística bosónica de las excitaciones del campo puede rastrearse hasta las reglas de cuantización utilizadas para este. Existen unas leyes de conmutación canónicas propias de todo sistema cuántico, que especifican el comportamiento del operador campo y su momento conjugado π(r). Estas implican que sus estados cuánticos son simétricos y corresponden a bosones. Puesto que los estados de múltiples fermiones deberían ser antisimétricos, para obtener un sistema de fermiones cuantizando un campo ψ, se imponen reglas con el signo incorrecto, es decir, de anti-conmutación. La elección de este signo —y con él, la estadística de las partículas resultantes— no es arbitraria, sino que existe una relación entre el espín y la estadística.
Espín y estadística
La teoría de campos concreta que es cuantizada determina las propiedades de las partículas que aparecen como sus modos normales. En particular, el tipo de campo determina el espín de las mismas. Algunos ejemplos son:[27]
- Un campo escalar que obedece la ecuación de Klein-Gordon resulta en una teoría de bosones de espín 0, como ciertos mesones.
- Un campo espinorial que obedece la ecuación de Dirac resulta en una teoría de fermiones de espín 1/2, como los electrones o los protones.
- Las ecuaciones del campo electromagnético —un campo vectorial— producen una teoría de bosones de espín 1, los fotones.
Estas teorías de campos son relativistas: sus ecuaciones correspondientes respetan la simetría Lorentz. Las partículas que aparecen en la versión cuántica de dichas teorías también lo son: se rigen por la cinemática relativista. De este modo, una teoría cuántica de campos es capaz de describir la dinámica de partículas cuánticas de acuerdo con la relatividad especial. Una teoría cuántica de campos también puede ser no relativista: es el caso por ejemplo de la ecuación del campo sonoro, que resulta en la teoría de los fonones.
Estos ejemplos respetan la relación empírica que existe entre el espín y la estadística de las partículas: el espín de un bosón —fermión— toma siempre valores enteros —semienteros—. Si se intenta la cuantización de un campo escogiendo la estadística contraria —por ejemplo cuantizando el campo escalar con reglas de anticonmutación, intentando obtener fermiones; o viceversa para el campo espinorial— se obtienen resultados físicamente inconsistentes.[28] Puede probarse que esto es general: en teoría cuántica de campos esta relación entre espín y estadística se demuestra como consecuencia directa de la unión entre mecánica cuántica y relatividad especial, el llamado teorema espín-estadística.[29]
Algunas de estas teorías de campos fueron investigadas inicialmente como ecuaciones de Schrödinger relativistas para un cuerpo, sin éxito. Esto motivó el nombre de segunda cuantización: los campos a los que se aplicaban las reglas de cuantización eran funciones de onda, obtenidas a su vez de aplicar esas reglas a una partícula puntual.[30]
Campo cuántico en interacción
Si la teoría de campos que se cuantiza es no lineal, las partículas que se obtienen interaccionan entre sí. En estas teorías las ecuaciones del campo son no lineales, involucrando productos de campos. De otro modo, la energía del sistema, representada por el operador hamiltoniano,[n 10] presenta un término de interacción —similar a un potencial V— no cuadrático: involucra productos de tres o más campos.[31] La gran mayoría de las teorías con interés para la física incluyen términos de interacción. La expresión siguiente para Hint (el potencial o hamiltoniano de interacción) proporciona diversos ejemplos:
- La interacción de Yukawa describe las fuerzas entre nucleones —neutrones y protones, campo Ψ— mediadas por mesones (piones de hecho, campo φ).[32] El término de interacción es proporcional a φΨΨ.
- El campo de Higgs media entre todas las partículas elementales masivas del modelo estándar. Viene representado por Φ y un bosón de espín 0 asociado. Los propios bosones de Higgs interaccionan entre sí, con un término dado por Φ4.
- La electrodinámica cuántica es la teoría cuántica que describe la interacción entre radiación —fotones, campo Aμ— y fermiones cargados —como electrones o quarks, descritos por un campo espinorial ψ—. El término de interacción es de la forma Aψψ.
Acompañando a cada producto de campos, hay una constante numérica, llamada constante de acoplo, que calibra lo intensa que es la interacción.[33] Por ejemplo, en el tercer término, e es la carga eléctrica del electrón.[32] En general no se conoce como calcular cantidades físicas —como probabilidades de colisión en un experimento de altas energías— de manera exacta en presencia de estos términos de interacción, lo que requiere aproximar el resultado de manera perturbativa.[34]
En una teoría de campos en interacción el número de partículas puede variar, lo que permite describir sistemas en los que el número de partículas presentes no es constante. Esto es debido a la presencia de los términos no cuadráticos: necesariamente contienen productos de operadores destrucción y creación en un número descompensado.[35] Otra consecuencia de la interacción entre campos cuánticos es la existencia de las antipartículas: si las partículas de un cierto sistema interaccionan entre sí y poseen alguna carga cuyo valor se conserva —como la carga eléctrica o la carga de color—, para poder describirlo mediante una teoría cuántica de campos relativista es necesario asumir la presencia de una «copia» para cada partícula, con idéntica masa pero carga opuesta.[36]
Enfoques alternativos
La descripción de la teoría cuántica de campos como la cuantización canónica de un campo y la subsecuente asociación a un sistema de partículas de número indeterminado es uno de los enfoques mayoritarios para definirla. Sin embargo existen otras maneras de presentar y estudiar la teoría. El formalismo de la integral de caminos es equivalente a la cuantización canónica, y puede tomarse como postulado inicial.[37] Otra posibilidad, en el contexto de la física de altas energías, es derivar las leyes más generales posibles que aúnen mecánica cuántica y relatividad especial, para describir el comportamiento de las partículas subatómicas. Estas leyes necesariamente toman la forma de una teoría cuántica de campos.[38] Ambas posibilidades son complementarias en cuanto a lo que consideran inicialmente más fundamental: el campo o las partículas.
Desde un punto de vista matemático, la teoría cuántica de campos no posee el mismo nivel de rigor que la mecánica cuántica más elemental. Esto ha motivado el interés de estudiarla con un enfoque formal o axiomático, intentando encontrar estructuras matemáticas completamente rigurosas que capturen sus características principales.[39] El caso particular del campo de Yang-Mills constituye el enunciado de uno de los problemas del milenio.
Existen también generalizaciones de la teoría cuántica de campos en distintos contextos. La teoría de campos a temperatura finita describe procesos termodinámicos con creación y destrucción de partículas, e incorpora modificaciones similares a las de la física estadística cuántica. La teoría cuántica de campos en espacio-tiempo curvo es el formalismo necesario para describir el campo cuántico en presencia de gravedad.
Aspectos clave
Diagramas de Feynman
Los experimentos de física de altas energías involucran habitualmente colisiones de partículas a altas velocidades.[40] La teoría cuántica de campos permite calcular los detalles de dichas colisiones, a partir de la probabilidad[n 11] M de que estas ocurran:
Esta expresión relaciona la probabilidad de encontrar las partículas β tras la colisión, partiendo de las partículas α,[n 12] en términos de S, la llamada matriz de scattering: un operador que recoge la evolución del sistema durante el experimento. Este operador puede obtenerse mediante un desarrollo perturbativo, en términos del hamiltoniano de interacción:[41]
,
donde se ha escrito explícitamente la constante de acoplo g. Este desarrollo supone que la interacción es débil o pequeña, frente a la probabilidad de no interacción.
Los diagramas —o reglas— de Feynman son una técnica para calcular dicha probabilidad de manera gráfica. Estos diagramas representan todos las posibles versiones subyacentes a un proceso dado: las partículas en interacción emiten o absorben un cierto número de partículas virtuales, que median las fuerzas entre ellas. Estos procesos virtuales ocurren debido a la incertidumbre inherente a una teoría cuántica. La energía necesaria para la aparición de estas partículas virtuales proviene de la relación de incertidumbre entre energía y tiempo:
- ,
de modo que estas «existen» por muy poco tiempo. En realidad, las partículas virtuales son solamente una abstracción y no pueden detectarse. El proceso físico real —la colisión— se entiende como una suma de todos estos procesos virtuales.[42] Por ejemplo, en el estudio de la dispersión Compton de un electrón por un fotón en electrodinámica cuántica —QED—, la amplitud cuántica viene dada por:
(3)
En estos diagramas, las líneas curvadas son fotones y las líneas rectas, electrones. El estado inicial y final son las líneas externas, iguales en todos los diagramas, puesto que todos corresponden al mismo experimento. La propagación de partículas se representa mediante líneas internas, y la emisión o absorción de un fotón por un electrón mediante vértices. Utilizando estos elementos, pueden escribirse todos los —infinitos— diagramas que contribuyen a este experimento.
La exactitud del cálculo aumenta con el número de vértices, que es igual a la potencia de la constante de acoplo en el desarrollo perturbativo. Así, los dos primeros diagramas del miembro derecho son proporcionales a e2 y el siguiente, a e4, donde e, la carga del electrón, es la constante de acoplo en QED. Las distintas versiones de la dispersión Compton pueden leerse cronológicamente en cada diagrama del miembro derecho de izquierda a derecha: en el primer diagrama, el electrón absorbe el fotón incidente y más tarde emite el fotón saliente; en el segundo, el electrón emite el fotón final y más tarde absorbe el fotón inicial; etc.
Los diagramas de Feynman son más que una técnica de cálculo, sino que constituyen la «piedra angular de la física de partículas».[43] Se consideran tan o más relevantes incluso que la propia teoría cuántica de campos de la que surgen, pues en ellos se reflejan los principios físicos subyacentes más importantes, y son la herramienta básica para analizar las colisiones relativistas.[44] Sin embargo, existen numerosos fenómenos en teoría cuántica de campos que no pueden ser analizados como una perturbación, como el confinamiento en QCD, o las soluciones no perturbativas.
Métodos funcionales. Soluciones no perturbativas
El formalismo de integral de caminos de la mecánica cuántica es un conjunto de reglas de cuantización alternativo que ofrece los mismos resultados que la cuantización canónica ordinaria. En este formalismo, todas las posibles trayectorias clásicas contribuyen a las amplitudes cuánticas:
(4)
En esta expresión, 〈x t|x' t'〉 es la probabilidad[n 11] de que la partícula se propague de x a x' entre los instantes t y t'; γ es una posible trayectoria entre dichos puntos del espacio-tiempo; y S[γ] es la acción de la partícula, un funcional de la trayectoria que determina las ecuaciones de movimiento clásicas.[45] En teoría cuántica de campos en particular, el formalismo de integral de caminos se usa habitualmente, permitiendo calcular la probabilidad de un proceso como una suma de las contribuciones de cada posible configuración del campo clásico.[n 13] La integral de caminos ofrece una serie de ventajas a la hora de obtener las reglas de Feynman y analizar las simetrías del sistema de forma directa, así como para aprovechar las analogías de la teoría cuántica de campos con la física estadística. Además, resulta indispensable para el análisis de las soluciones no perturbativas de la misma.[46]
El desarrollo perturbativo utilizado en las teorías de campos en interacción —por ejemplo, a la hora de calcular diagramas de Feynman— se basa en corregir las soluciones más triviales, las ondas planas de un campo libre, considerando los términos de interacción como una perturbación pequeña comparada con estas. Sin embargo, en algunas teorías existen soluciones no perturbativas: soluciones de las ecuaciones de campo en las que las correcciones de la interacción no son pequeñas, y que no pueden ser aproximadas a través del citado desarrollo perturbativo. Todas las configuraciones clásicas del campo contribuyen a las amplitudes cuánticas, como se deduce de (), luego dichas soluciones se han de tener en consideración.[46] Existen muchas clases de soluciones no perturbativas con diferentes efectos físicos:[47]
- Los solitones u ondas solitarias son soluciones de ecuaciones de ondas no lineales que se propagan sin alterar su forma. Una teoría de campos con soluciones solitónicas presenta dos tipos de partículas al ser cuantizada: aquellas asociadas con sus modos normales —las mencionadas soluciones triviales corregidas—; y aquellas asociadas a las soluciones solitónicas, cuyas masas en general dependen de manera no analítica de las masas y constantes de acoplo del campo, como por ejemplo MS = m / g.[48] Esto implica en particular que en el régimen de interacción débil —g pequeño— la masa del solitón es grande comparada con la de las partículas ordinarias —ya que 1 / g es grande—.
- Los instantones son soluciones de la versión euclídea de unas ecuaciones de campo dadas —en las que la variable tiempo se sustituye por una coordenada espacial adicional— localizadas alrededor de un punto. Vistas desde el punto de vista de la teoría original dichas soluciones están concentradas alrededor de un evento —un punto del espacio-tiempo—, de ahí su nombre. Los instantones son responsables de multitud de efectos como ciertas anomalías axiales, confinamiento en algunos modelos sencillos o la (ausente) violación de CP en la cromodinámica cuántica.
Otros ejemplos incluyen monopolos magnéticos, vortex lines, domain walls, skyrmiones, etc.
Renormalización
En las aplicaciones tempranas de la teoría cuántica de campos se constató que al utilizarla para calcular ciertas cantidades arroja un valor infinito. Este resultado aparece a menudo al aumentar la precisión de un cálculo cualquiera, más allá del orden más bajo de aproximación en la serie perturbativa.[50] Por ejemplo, el tercer diagrama de la dispersión Compton, mostrado en (), es divergente: su valor es infinito.[51]
La renormalización es un método que se desarrolló para extraer de estas divergencias las cantidades finitas susceptibles de medirse experimentalmente. La solución del problema pasa por reconocer que en los cálculos perturbativos se extrapola la teoría a distancias arbitrariamente cortas —o equivalentemente, a energías arbitrariamente altas—,[n 14] de ahí el nombre de divergencias ultravioletas. Por ejemplo, el tercer diagrama de la dispersión Compton en () contiene una parte denominada la auto-energía del electrón Σ, dada por:

en la que un fotón virtual es emitido y reabsorbido por un electrón. Sumar sobre todas las versiones virtuales de la dispersión Compton implica sumar la contribución de cada diagrama pero además, en este en particular, sumar sobre todos los posibles valores de energía y momento del fotón virtual, mediante la expresión:
(5),
que es divergente.[51] Al identificar dicha extrapolación como la fuente del resultado infinito, se puede examinar qué parte del mismo corresponde verdaderamente a la cantidad física, cuyo valor es necesariamente finito. En particular los infinitos desaparecen al considerar que deben absorberse en los parámetros de la teoría.
En el ejemplo de la auto-energía Σ, el proceso es el siguiente. Primero, se pasa a utilizar una teoría regularizada, una versión inexacta de la teoría original pero libre de divergencias, cuyos resultados solo pueden ser una aproximación. En esta teoría regularizada se hace patente que las constantes m0 y e0 de la ecuación (), la masa y la carga del campo, no se corresponden con la masa y la carga del electrón. Es decir, la presencia de la interacción establece una diferencia entre los parámetros físicos de las partículas y los parámetros del campo —denominados «desnudos»— utilizados en los cálculos. Establecida la relación entre ellos, puede reescribirse la fórmula () en términos de los verdaderos parámetros físicos, y se comprueba entonces que es finita.[52]
Este proceso posee además cierta ambigüedad. La sustracción de dos cantidades divergentes para obtener una diferencia finita no determina por completo esta última, sino que depende de la definición de los parámetros físicos que se adopte. Para ello existe más de un criterio posible, como por ejemplo expresar los resultados en función no de la carga eléctrica e, sino de la carga efectiva a una energía dada, e(E). Estos parámetros alternativos son «constantes móviles»,[n 15] es decir que varían con la energía y ofrecen ciertas ventajas a la hora de realizar cálculos en distintas escalas de energía.
Esta técnica, llamada grupo de renormalización,[n 16] no sólo es de utilidad práctica, sino que aporta una visión nueva del papel de las divergencias y de la teoría de campos en general. Así, la renormalización puede ser entendida como el proceso de aislar los grados de libertad relevantes para un proceso físico, ignorando contribuciones demasiado remotas en energía.[53]
El proceso de absorber los infinitos en los parámetros de una teoría no puede llevarse a cabo siempre. Las teorías para las que esto sí es posible son llamadas renormalizables, como por ejemplo las interacciones del modelo estándar. La interacción gravitatoria, sin embargo, es un ejemplo de teoría no renormalizable: para reabsorber todos sus infinitos hace falta considerar un número infinito de parámetros. Las teorías no renormalizables tienen menos poder de predicción, pero aun así se utilizan a menudo como teorías efectivas.[54]
Teorías gauge
Una teoría gauge es una teoría cuántica de campos con una cierta estructura que mimetiza la de la electrodinámica cuántica (o QED). QED es la versión cuántica de la electrodinámica clásica, que describe la interacción entre cargas eléctricas y radiación. En QED, las cargas eléctricas interaccionan mediante el intercambio de fotones, los cuantos del campo electromagnético.
Las ecuaciones clásicas de la electrodinámica poseen una propiedad denominada invariancia gauge,[n 17] de forma que de cada solución para el potencial electromagnético Aμ se puede obtener otra, Aμ + ∂μρ, sin más que añadir el gradiente de una función arbitraria del espacio y el tiempo, ρ(t,x). Sin embargo todos estos potenciales distintos corresponden a un único campo electromagnético. A esta propiedad se la denomina simetría local, ya que la transformación de las soluciones varía según el punto del espacio-tiempo, es decir, según el valor de ρ, y es indispensable a la hora de aplicar las reglas de cuantización de forma consistente y obtener QED.[55]
Una teoría gauge no abeliana es una versión más general de QED. En ellas, las partículas poseen múltiples cargas que, como la carga eléctrica, se mantienen constantes. Estas partículas cargadas interaccionan entre sí mediante el intercambio de varios bosones gauge intermediarios —parecidos al fotón—. Sin embargo, en el caso no abeliano, los bosones intermediarios también poseen carga e interaccionan entre sí, a diferencia del caso de QED, donde el fotón no está cargado eléctricamente y no interacciona consigo mismo. Los bosones gauge son no masivos en general, aunque el fenómeno de ruptura espontánea de simetría puede dotarlos de masa. Las teorías gauge no abelianas se obtienen cuantizando las ecuaciones de un campo de Yang-Mills Aμa.[n 18] Estas son similares a las del campo electromagnético, aunque más complejas —son no lineales—, y también tienen una propiedad de invariancia gauge parecida a la de las ecuaciones de Maxwell. Un ejemplo de teoría gauge no abeliana es la cromodinámica cuántica (véase imagen).
Las teorías gauge son una parte esencial de la formulación del modelo estándar de las partículas fundamentales, que es precisamente una teoría gauge basada en tres grupos de simetría. A nivel cuántico poseen rasgos únicos que las hacen interesantes, como el confinamiento y la libertad asintótica en algunos casos, o la ausencia de bosones de Goldstone en una ruptura espontánea de simetría. La relatividad general puede ser entendida también como una teoría gauge, asociada a la conservación de la energía y el momento.
Simetrías. Ruptura espontánea y anomalías
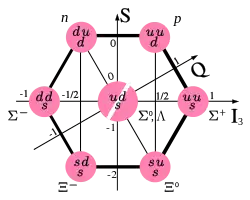
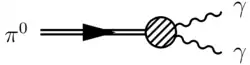
Las simetrías tienen un papel fundamental en la física. Si las ecuaciones de movimiento de un sistema son invariantes bajo un cierto grupo de transformaciones, una consecuencia general es la existencia de cantidades conservadas. En teoría cuántica de campos las simetrías son también una herramienta crucial. En una teoría relativista, la invariancia Lorentz determina las posibles especies de partículas en función de su masa y espín. Las simetrías bajo transformaciones internas tales como un cambio de fase o una transformación unitaria de los campos, implican la conservación de cantidades como la carga eléctrica, el isoespín, la carga de color, etc. Incluso cuando una simetría no es exacta —las ecuaciones sí cambian bajo sus transformaciones—, puede ser útil asumirla como cierta dentro de cierto rango de aproximación adecuado, si con eso se consigue un entendimiento cualitativo de algún fenómeno.[57] Es el caso por ejemplo de la conservación del sabor en las colisiones a altas energías. Además de simetrías exactas y aproximadas, pueden darse otras dos posibilidades de interés: ruptura espontánea de simetría y anomalías.
El fenómeno de la ruptura espontánea de simetría[n 19] es común a todos los sistemas cuánticos con infinitos grados de libertad, como la teoría cuántica de campos.[58] Una simetría espontáneamente rota es aquella que, siendo exacta, no muestra efectos evidentes, puesto que los estados de mínima energía del sistema no son invariantes bajo dicha simetría. Su presencia se manifiesta indirectamente por la aparición de unas partículas conocidas como bosones de Goldstone; o por la presencia de bosones gauge masivos, si la simetría involucrada es una simetría local, es decir, asociada con una teoría gauge.
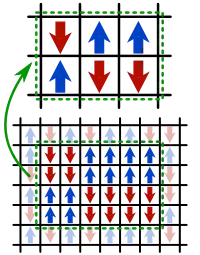
- Un ejemplo común de ruptura espontánea de simetría se da en un material ferromagnético: por debajo de cierta temperatura, el vector de magnetización del material apunta en una determinada dirección en el espacio. Aunque las leyes físicas involucradas son invariantes bajo rotaciones, en el estado de mínima energía la magnetización de cada dominio magnético apunta en una misma dirección. En este sistema se producen excitaciones colectivas conocidas como magnones u ondas de espín, que se corresponden con los bosones de Goldstone de la simetría espontáneamente rota.[59]
- La ruptura espontánea de simetría tiene un papel crucial en el modelo estándar de la física de partículas, a través del mecanismo de Higgs, un elemento de dicho modelo. La fuerza electrodébil parece explicarse con facilidad mediante una teoría gauge, cuya simetría correspondiente prohíbe que las partículas con carga débil posean masa, cuando de hecho la tienen. Estas masas no nulas son análogas a la dirección de la magnetización de un material ferromagnético en cuanto a que corresponden al valor del campo de Higgs a baja energía. En particular, los bosones W± y Z0, intermediarios de la interacción débil, son también masivos.
Las anomalías son violaciones de una simetría en un sistema cuántico obtenido a partir de un sistema clásico que sí poseía esta simetría. Son muy frecuentes en las teorías cuánticas de campos pues, como parte del proceso de renormalización, estas han de ser regularizadas para lidiar con sus resultados infinitos. Este paso intermedio en general viola las simetrías de la teoría, y no siempre es posible restablecerlas en la teoría renormalizada.[60]
- La llamada anomalía conforme ocurre de forma habitual,[61] en teorías que clásicamente son invariantes bajo dilataciones; es decir, cuyo comportamiento es el mismo independientemente de las distancias físicas involucradas, o de las energías.[n 14] En general esta simetría no permanece en la teoría cuántica, donde la intensidad de las fuerzas varía con la energía.
- La anomalía denominada axial está relacionada con los números cuánticos conservados en el sistema. Por ejemplo, en la versión clásica del modelo estándar, tanto el número leptónico como el número bariónico son cargas conservadas.[n 20] Sin embargo, se demuestra que existen fenómenos no perturbativos que permiten una variación de ambos números.[62]
Las anomalías pueden representar una inconsistencia en la teoría si afectan a una simetría gauge, dado que estas son fundamentales para eliminar grados de libertad no físicos del sistema.[60]
Simetrías discretas. CPT
Algunas simetrías discretas tienen un papel especial en teoría cuántica de campos, en particular en el contexto de la física de partículas, debido al descubrimiento de que algunas interacciones fundamentales no respetan la paridad ni la conjugación de carga. Esto significa que se comportan de manera diferente si se aplica una transformación especular, que resulta equivalente a visualizarlas en un espejo o cambiar cada partícula por su antipartícula correspondiente. Estas simetrías está relacionadas con la simetría de inversión temporal, determinante del comportamiento de las interacciones al cambiar la dirección del tiempo, a través del denominado teorema CPT, que asegura que la combinación de las tres operaciones deja inalterado cualquier sistema relativista cuántico.[63]
Aplicaciones
Física de altas energías


En el ámbito de la física de altas energías se estudian los componentes elementales de la materia y sus interacciones. Para ello es necesario utilizar una gran cantidad de energía en relación con el número de partículas involucradas y así descomponer la materia. En este régimen, es inevitable el uso de una teoría cuántica de campos para dar cuenta de la cinemática relativista de las partículas.
En la actualidad, la teoría denominada modelo estándar recoge los fenómenos conocidos a escala subatómica. Esta teoría clasifica todos los constituyentes fundamentales de la materia en tres familias de quarks, componentes de los hadrones como el protón y el neutrón; y de leptones: el electrón y partículas similares, junto con los neutrinos. Todas estas partículas son fermiones de espín 1/2 y, a excepción de los neutrinos, están cargadas eléctricamente. Además todas tienen masa, aunque el descubrimiento de las masas (extremadamente pequeñas) de los neutrinos es reciente aún, y no se incluye en el modelo estándar.[64]
El modelo estándar es una teoría gauge: las interacciones entre estas partículas ocurren mediante el intercambio de bosones gauge de espín 1. Todas salvo los neutrinos interaccionan electromagnéticamente a través del fotón. Los quarks poseen carga de color, y pueden intercambiarse gluones. Además, todos estos fermiones poseen una carga denominada isoespín débil, que hace que interaccionen entre sí a través de los bosones débiles Z0 y W± los cuales, a diferencia de los fotones y gluones, tienen masa. Estas tres interacciones se conocen como la interacción electromagnética, la interacción fuerte y la interacción débil.
El modelo estándar incluye una partícula de espín 0 y sin carga denominada bosón de Higgs cuya existencia está parcialmente confirmada,[n 21] y que interaccionaría con todas las que tienen masa, incluida ella misma.[n 22] Su presencia explica precisamente las masas no nulas de las partículas, que en apariencia contradicen la conservación del isoespín débil.
El modelo estándar ha alcanzado un alto grado de precisión en sus predicciones, aunque existen múltiples fenómenos que no explica, como el origen de la masa de los neutrinos, la naturaleza de la materia oscura, la interacción gravitatoria, etc.[65] Tampoco existe una explicación teórica satisfactoria del comportamiento de los quarks dentro de los hadrones que forman a baja energía, más allá de cálculos aproximados utilizando una versión discretizada de la teoría de campos.[66]
Física de la materia condensada
El ejemplo básico del formalismo de segunda cuantización pertenece a la disciplina de la física del estado sólido: la descripción de las oscilaciones de los átomos en un sólido como cuasipartículas llamadas fonones. En física de la materia condensada existen muchos sistemas que se analizan términos similares, aprovechando la comodidad de las técnicas de many body («muchos cuerpos»), aun cuando la creación y destrucción de partículas no necesariamente se dé en realidad. La teoría de campos permite describir de manera efectiva las excitaciones colectivas de un sistema de muchas partículas en una fase dada.[67]
Algunos ejemplos de problemas en los que se aplica son la teoría BCS de la superconductividad, el efecto Hall cuántico o el ferromagnetismo y antiferromagnetismo. Muchos de los aspectos característicos de la teoría cuántica de campos están involucrados en estos fenómenos: ruptura espontánea de simetría, invariancia gauge, modelos sigma no lineales, etc.[68]
Parte de estas propiedades de la teoría cuántica de campos se descubrieron o plantearon inicialmente en el contexto de la física de la materia condensada. El concepto de ruptura espontánea de simetría fue desarrollado para explicar la superconductividad antes de ser adaptado al mecanismo de Higgs. La técnica del grupo de renormalización, donde se examina el cambio en los parámetros de una teoría dependiendo de la escala a la que se la examine, aparece de manera natural en materia condensada al analizar, por ejemplo, el modelo de Ising.[7]
Véase también
Notas
- La palabra «partícula» se utiliza en mecánica cuántica a nivel introductorio para enfatizar al comportamiento clásico de un punto material, frente al comportamiento ondulatorio de la luz. Las partículas microscópicas, como los átomos o los fotones, presentan un comportamiento intermedio, caracterizado por la dualidad onda-corpúsculo. Mientras no se diga lo contrario, en este artículo la palabra «partícula» —y sin excepción, «partícula cuántica»— se refiere a este segundo significado.
- No confundir con «teoría clásica de campos».
- Esta interpretación no es la única posible, pero sí la más extendida. Véase Interpretaciones de la mecánica cuántica.
- Esta evolución es determinista mientras no el sistema no se vea alterado por una medida —cuyo resultado es no determinista—. Véase Ynduráin, 2003, §2.2.
- El nombre viene del griego , «voz», por la relación de estos cuantos con las ondas sonoras.
- Para el origen de este nombre, véase Espín y estadística.
- Se ignora en este párrafo la constante aditiva ℏω/2. La fórmula correcta puede encontrarse en Ynduráin, 2003, §7.2 o Sakurai, 1994, §2.3.
- Esta conservación del número de partículas es consecuencia de las ecuaciones de movimiento concretas del campo libre (para el campo en interacción no ocurre). Esto contrasta con la mecánica cuántica «ordinaria», donde la conservación es un requerimiento intrínseco de cualesquiera ecuaciones de movimiento se planteen.
- La cuantización de los campos libres, escalar, espinorial o vectorial, puede encontrarse en multitud de referencias, como Nair, 2005,Peskin y Schroeder, 1995 o Sterman, 1993.
- O, de forma equivalente, el lagrangiano.
- En realidad, se trata de una amplitud de probabilidad: un número complejo z cuyo módulo al cuadrado es la probabilidad propiamente dicha, P = |z|2.
- α y β describen una colección de diversas partículas, no necesariamente las mismas al principio y al final, en distintos estados de movimiento. Se obvian en el texto los detalles de la fórmula correcta. Véase Weinberg, 1995, §3.2.
- Para utilizar esta técnica en el caso de campos fermionicos, es necesario considerar unos «números anticonmutativos» —que cumplen ξθ = −θξ dados ξ y θ números cualesquiera—, denominados números de Grassmann.
- Téngase en cuenta que la energía de una partícula proporciona una escala de longitud: su longitud de onda de De Broglie .
- «Running coupling constants».
- A pesar del nombre, no guarda ninguna relación con la teoría de grupos. Véase Weinberg, 1996, p. 111.
- Pronunciado [ɡeɪdʒ], «calibre» en inglés.
- La cuantización del campo de Yang-Mills resulta en una teoría de bosones gauge en interacción. Pueden añadirse otras partículas cargadas, como fermiones, cuantizando otros campos acoplados a este.
- El nombre es engañoso, ya que a fin de cuentas la simetría es exacta. Véase Coleman, 1985, 116.
- Es decir, dichas simetrías son respetadas en el lagrangiano del modelo estándar.
- El 13 de marzo de 2013 el CERN confirmó provisionalmente la existencia de una partícula muy similar al Higgs. Véase O'Luanaigh, C. (14 de marzo de 2013). «New results indicate that new particle is a Higgs boson». CERN. Consultado el 4 de diciembre de 2013.
- Para la masa de los neutrinos se consideran otras posibilidades, como una mezcla de masa «ordinaria» —masa de Dirac, proveniente de su interacción con el Higgs— con masa de Majorana, responsable de una hipotética violación del número leptónico. Véase Langacker, 2010, §7.7.
Referencias
- Nair, 2005, p. 7.
- Itzykson y Zuber, 1980, p. 107.
- Nair, 2005, p. VII.
- Ver Peskin y Schroeder, 1995, p. 198.
- Esta primera parte —hasta 1950— está basada en Weinberg, 1995, §1.
- Cao, 1997, §9.2.
- Véase Zee, 2003, §VI.8 y Steven Weinberg. «From BCS to the LHC» (en inglés). Archivado desde el original el 12 de marzo de 2012. Consultado el 12 de marzo de 2012.
- Cao, 1997, p. 323.
- Weinberg, 1996, §18.7.
- Zee, 2003, §V.6.
- La cita aparece en Kuhlmann, 2009, §3.4. Véase también Zee, 2003, §VIII.3
- Ynduráin, 2003, §4.7
- Véase Zee, 2003, p. 3 y la Introducción de Ynduráin, 1989.
- Sakurai, 1967, §1-1.
- Itzykson y Zuber, 1987, p. 47.
- Ver Weinberg, 1995, p. 11.
- Peskin y Schroeder, 1995, §2.1.
- Peskin y Schroeder, 1995, §2.3.
- Esta parte está referida a sistemas sencillos con ecuaciones de movimiento lineales. Véase Goldstein, 1998, §12.1.
- Bogoliubov, Nikolay; Shirkov, Dmitry (1982). Quantum fields (en inglés). Benjamin-Cummings Pub. Co. p. 8. ISBN 0-8053-0983-7.
- En el caso del campo, al tomar el límite continuo, los modos normales pueden ser continuos a su vez. Véase Ynduráin, 2003, §7.5.3 y §19 para esta parte.
- Weinberg, 1995, §3.1
- Weinberg, 1995, p. 31
- Abrikosov, A.A. (1965). «I, §3. Second quantisation». Methods of quantum field theory in statistical physics (en inglés). Pergamon Press. OCLC 222056583..
- Sakurai, 1967, p. 27.
- Peskin y Schroeder, 1995, p. 22.
- Nair, 2005, p. 8.
- Como estados de energía negativa o probabilidades negativas. Véase Nair, 2005, p. 31.
- Véase Weinberg, 1995, §5.7 y una de las primeras demostraciones en Pauli, Wolfgang (1940), «The connection between spin and statistics», Physical Review (en inglés) 58, pp. 716-722, consultado el 19 de junio de 2011..
- Véase Peskin y Schroeder, 1995, p. 19. Esta denominación, de uso estándar en física, puede resultar confusa (véase Weinberg, 1995, pp. 19,28).
- Zee, 2003, §I.7.
- Peskin y Schroeder, 1995, §4.1
- Nair, 2005, p. 55.
- Ynduráin, 1989, §8.1.
- Véase Srednicki, Mark Allen (2007). Quantum field theory (en inglés). Cambridge University Press. p. 12. ISBN 9780521864497. Esto implica que el hamiltoniano y el operador número de partículas no conmuten en el caso no cuadrático. De ahí que el número de partículas no se mantenga constante, ya que las leyes de conservación cuánticas requieren la conmutación con el hamiltoniano. Véase Cohen-Tannoudji, Claude; Diu, Bernard; Laloe, Frank (1991). «Chapter III: The postulates of quantum mechanics». Quantum mechanics (en inglés). Wiley-Interscience. ISBN 0-471-16433-X, §D-2-c.
- Weinberg, 1995, p. 199.
- Véase Peskin y Schroeder, 1995, p. 283 y Weinberg, 1995, p. 384.
- Véase el Preface de Weinberg, 1995.
- Kuhlmann, 2009, §4.1.
- Véase la introducción de Weinberg, 1995, §3 y el comienzo de Peskin y Schroeder, 1995, §4.5.
- Se obvian en el texto los detalles de la fórmula de la serie de Dyson. Véase Peskin y Schroeder, 1995, p. 85.
- Peskin y Schroeder, 1995, p. 191.
- La cita aparece en Martin, Brian Robert; Shaw, Graham (2008). Particle physics (en inglés). John Wiley and Sons. p. 9. ISBN 9780470032930.
- Véase la Introduction de Veltman, Martinus (1994). Diagrammatica. The path to Feynman rules (en inglés). Cambridge University Press. ISBN 0521456924, y el Preface de Bjorken, James D.; Drell, Sidney D. (1965). Relativistic quantum fields (en inglés). McGraw-Hill. ISBN 9780070054943.
- Sakurai, 1994, p. 258.
- Véase la introducción de Weinberg, 1995, §9 y de Peskin y Schroeder, 1995, §9.
- Para esta parte, véase Rajaraman, 1989, §1 y Weinberg, 1996, §23.
- Nair, 2005, p. 468.
- Peskin, 1995, p. 255.
- Cao, 1997, p. 186.
- Véase Peskin y Schroeder, 1995, p. 216 y en adelante.
- Para una exposición más detallada, véase Nair, 2005, §9.5.
- Véase para el grupo de renormalización, la introducción de Weiberg, 1996, §18.
- Véase por ejemplo Weinberg, 1995, §12.3.
- Esto es debido a que en la cuantización aparecen polarizaciones no físicas para el fotón. Véase Itzykson y Zuber, 1980, §3-2-1.
- En particular, una parte de esta simetría asegura la conservación del número fermiónico axial U(1)A, que se violaría en dicho proceso. La anomalía no afecta a toda la simetría —no empeora las diferencias de masa de los bariones ligeros comentadas previamente—, sólo a esta corriente axial. Véase Weinberg, 1996, §22.1 para los detalles de este proceso.
- Donoghue, John; Golowich, Eugene; Holstein, Barry (1992). Dynamics of the Standard Model (en inglés). Cambridge University Press. p. 13. ISBN 0521476526.
- Itzykson y Zuber, 1980, p. 525.
- Véase para este ejemplo Zee, 2003, p. 199 y Coleman, 1985, §2.1.
- Nair, 2005, §13.1.
- Véase la introducción en Collins, John C. (1984). «13. Anomalies». Renormalization (en inglés). Cambridge University Press. ISBN 0-521-24261-4.
- Dicha variación no perturbativa es tal que ambos incrementos siempre se compensan entre sí: ni el número de bariones B ni el de leptones L son conservados —aunque por muy poco—, pero sí lo es su diferencia B − L. Véase Weinberg, 1996, p. 454.
- Weinberg, 1995, §5.8.
- Véase la introducción de Langacker, 2010, §7.7.
- Véase el Preface de Langacker, 2010.
- Peskin y Schroeder, 1995, §22.1
- Véase el Preface de Altland, Alexander; Simons, Benjamin D. (2010). Condensed matter field theory (en inglés). Cambridge University Press. ISBN 9780521769754.
- Puede encontrarse una exposición completa en Zee, 2003, §V y §VI.
Bibliografía
- Cao, Tian Yu (1997). Conceptual developments of 20th century field theories (en inglés). Cambridge University Press. ISBN 0521431786.
- Coleman, Sidney (1985). Aspects of symmetry (en inglés). Cambridge University Press. ISBN 0521318270.
- Goldstein, Herbert (1998). Mecánica clásica. Editorial Reverté. ISBN 978-84-291-4306-5.
- Itzykson, Claude; Zuber, Jean-Bernard (1980). Quantum field theory (en inglés). McGraw-Hill International Book Co. ISBN 0-07-032071-3.
- Langacker, Paul (2010). The Standard Model and beyond (en inglés). CRC Press. ISBN 978-1-4200-7906-7.
- Kuhlmann, Meinard. «Quantum field theory». En Edward N. Zalta, ed. The Stanford Encyclopedia of Philosophy (Spring 2009 Edition). Archivado desde el original el 12 de marzo de 2012. Consultado el 12 de marzo de 2012.
- Nair, V. Parameswaran (2005). Quantum field theory: a modern perspective (en inglés). Springer Science. ISBN 0-387-21386-4.
- Peskin, Michael; Schroeder, Daniel (1995). An introduction to quantum field theory (en inglés). Westview Press. ISBN 0-201-50397-2.
- Rajaraman, R. (1989). Solitons and instantons (en inglés). North-Holland. ISBN 0-444-87047-4.
- Sakurai, Jun John (1967). Advanced quantum mechanics (en inglés). Addison-Wesley Publishing Company. ISBN 978-0201067101.
- Sakurai, Jun John (1994). Modern quantum mechanics (en inglés). Addison-Wesley Publishing Company. ISBN 0-201-53929-2.
- Sterman, George (1993). An introduction to quantum field theory (en inglés). Cambridge University Press. ISBN 0521322588.
- Weinberg, Steven (1995). The quantum theory of fields I: Foundations (en inglés). Cambridge University Press. ISBN 0-521-55001-7.
- Weinberg, Steven (1996). The quantum theory of fields II: Modern applications (en inglés). Cambridge University Press. ISBN 0-521-55002-5.
- Zee, A. (2003). Quantum field theory in a nutshell (en inglés). Princeton University Press. ISBN 0-691-01019-6.
- Ynduráin, Francisco José (2003). Mecánica cuántica (2ª edición). Ariel. ISBN 84-344-8060-3.
- Ynduráin, Francisco José (1989). Mecánica cuántica relativista (con una introducción a la teoría cuántica de campos). Alianza Editorial. ISBN 978-84-206-8129-0.
Bibliografía adicional en español
- Dirac, Paul A.M. (1968). Principios de mecánica cuántica. Ariel. Depósito legal: B 18229-1968.
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. (1971). Teoría cuántica relativista, 1. Curso de física teórica. Volumen 4. Editorial Reverté. ISBN 978-84-291-4084-2.
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. (1981). Teoría cuántica relativista, 2. Curso de física teórica. Volumen 5. Editorial Reverté. ISBN 978-84-291-4085-9.
- Kittel, Charles (1997). Introducción a la física del estado sólido (3ª edición). Reverté. ISBN 84-291-4317-3.
Enlaces externos
 Wikilibros alberga un libro o manual sobre Teoría cuántica de campos.
Wikilibros alberga un libro o manual sobre Teoría cuántica de campos.- Fields por Warren Siegel (gratis; 800 páginas).