Poliedro uniforme dual
Un poliedro uniforme dual es el conjugado de un poliedro uniforme. Cuando un poliedro uniforme es isogonal, entonces su correspondiente poliedro uniforme dual es isoedral.
Enumeración
Los poliedros de con la propiedad de ser cara-transitivos comprenden el conjunto de 9 poliedros regulares, dos conjuntos finitos que comprenden 66 poliedros no regulares y dos conjuntos infinitos:
- 5 sólidos platónicos convexos regulares, que son duales entre sí (el tetraedro regular es su propio dual).
- 4 sólidos de Kepler-Poinsot con forma de estrellas regulares, que son duales entre sí.
- 13 sólidos de Catalan convexos, que son duales a los sólidos arquimedianos convexos uniformes.
- 53 poliedros estrellados, que son los duales de los poliedros uniformes estrellados.
- La serie infinita de bipirámides, que son duales de los prismas uniformes, tanto convexas como en estrella.
- La serie infinita de trapezoedros, que son duales a las de antiprismas uniformes, tanto convexos como en estrella.
Magnus Wenninger describió el conjunto completo, junto con instrucciones para construir los correspondientes modelos, en su libro Dual Models.
Construcción de Dorman Luke
Para un poliedro uniforme, cada cara del poliedro dual puede derivarse de la figura de vértice correspondiente del poliedro original usando la construcción Dorman Luke.[1]
Como ejemplo, la siguiente ilustración muestra la figura de vértice (en rojo) del cuboctaedro, que se usa para derivar la cara correspondiente (en azul) del rombododecaedro.
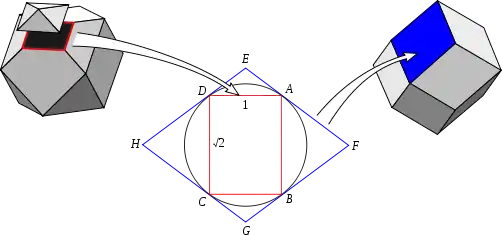
La construcción de Dorman Luke procede de la siguiente manera:
- Marcar los puntos A, B, C, D de cada arista conectada al vértice V (en este caso, los puntos medios) de manera que VA = VB = VC = VD.
- Dibujar la figura de vértice ABCD.
- Dibujar el circuncírculo de ABCD.
- Dibujar las rectas tangentes al circuncírculo en cada esquina A, B, C, D.
- Marcar los puntos E, F, G, H donde se encuentran cada dos rectas tangentes adyacentes.
Los segmentos de recta EF, FG, GH, HE ya están dibujados, como partes de las rectas tangentes. El polígono EFGH es la cara del poliedro dual que corresponde al vértice original V.
En este ejemplo, el tamaño de la figura de vértice se eligió de modo que su circunferencia se encuentre en la interesfera del cuboctaedro, que también se convierte en la interesfera del dodecaedro rómbico dual. La construcción de Dorman Luke solo se puede usar cuando un poliedro tiene tal interesfera, de modo que la figura de vértice tiene un círculo circunscrito. Por ejemplo, se puede aplicar a los poliedros uniformes.
Véase también
Referencias
- Cundy y Rollett (1961), p. 117;Wenninger (1983), p. 30.
Bibliografía
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd edición), Oxford: Clarendon Press, MR 0124167..
- Gailiunas, P.; Sharp, J. (2005), «Duality of polyhedra», International Journal of Mathematical Education in Science and Technology 36 (6): 617-642, S2CID 120818796, doi:10.1080/00207390500064049..
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-54325-8.